比赛流程体验，依托，开赛几分钟了，选手还卡在门外无法入场，也没给延时，说好的桌上会发三支笔，于是我们就没准备，要了三次笔，终于在一小时后拿到了😅
比赛题目体验，依托，签到卡住了，4题金到铜，100多队0题

前提：
打星旅游队，配置是三个退役老登，最后3题，由于少了许多有效队伍，我们大概铜牌位置。

正文记录：
前面一直在看过的最多的两道G和I，2两小时12分才过第一道题G，太菜了

题意是，若干询问（T $\le$ 10）[L, R]区间中最大的gcd(x,y),其中$L\le x<y\le R,L,R\in 属于[1,1e12]$
转化就是求最大的g，满足存在一个k使得 $L\le gk<g(k+1)\le R$，即$\frac{L}{k}\le g\le \frac{R}{k+1}$，分别枚举g和k从1至1e6，check即可

I题题意是若干如$a_i\ge a_j+a_k$的限制，构造a数组使得min($\sum a$)。
宇鹏看完后提出拓扑+贪心的构造，1h37交了一发wa了，2h时发现重边和爆int的情况，遂交第二发再次喜提wa，而后思宇看了下发现做法一开始就假了，若有条件$a_1\ge a_2+a_3,a_1\ge a_4+a_5$，其实$a_1=2$是最小的，之前的做法求出来是4，修了下过了

C题题意，给一棵以1为根的树，每个点有权值$w_i$，找最优的dfs序，求$max(\sum p_i{w}_i)$，其中p为dfs序
一开始没看到以1为根，以为是无根树，口了下以1为根递归先求最优，再换根dp，然后发现换根算贡献不会算，经过思宇提醒后发现是有根树，浪费了有二十分钟🤡
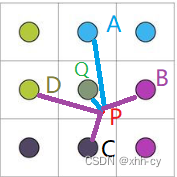
如下图，当前根为rt,假设dfs时先选择以i为根的子树，再选以j为根的子树是最优的顺序，则有贡献

$(siz[rt]-1-siz[i])\ast f[i]+(siz[rt]-1-siz[i]-siz[j])\ast f[j]$
若先选j再选i，则有贡献
$(siz[rt]-1-siz[j])\ast f[j]+(siz[rt]-1-siz[j]-siz[i])\ast f[i]$
展开后发现不同项为$-siz[i]\ast f[j]>-siz[j]\ast f[i]$,即$\frac{siz[i]}{f[i]}<\frac{siz[j]}{f[j]}$，按照这个顺序选择子树即可。
然后又在赋值$p_i$这里卡了有半小时，最后想了下重新建树好了，过题时3h52，快封榜了。。。思维迟钝太多了

E题题意，给n和z，n个人俩俩比赛，赢的人加一分，输的不扣分，没有平局的结果。约定任意z个人，一定存在一人和其他人比赛结果全胜，还有一人全输。问最少有多少种不同的分数结果$z\le n$

看懂题意我都花了好几分钟，直接思考我没啥思路。宇鹏说了些小结论，一定不存在z元环，之后队友们开始找规律，还剩五分钟时开始打规律，最后剩个else没打完。。。赛后和师弟对了下，还真是找规律，结论也对的，但凡给早点进场或者延期都a了💩。

自己确实菜，但比赛体验也太糟糕了。