欢迎光临:
男神
目录
一·树的介绍和表示:
二·二叉树的介绍及性质:
三·堆的介绍及创建:
1·堆的创建:
2·堆的应用:
四·二叉树的创建:
①// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树BTNode*BinaryTreeCreate(BTDataType* a, int n, int* pi):
②void BinaryTreeDestory(BTNode** root):
③int BinaryTreeSize(BTNode* root):
④int BinaryTreeLeafSize(BTNode* root):
⑤int BinaryTreeLevelKSize(BTNode* root, int k):
⑥BTNode* BinaryTreeFind(BTNode* root, BTDataType x):
⑦void BinaryTreePrevOrder(BTNode* root):
⑧void BinaryTreeInOrder(BTNode* root):
⑨void BinaryTreePostOrder(BTNode* root):
⑩void BinaryTreeLevelOrder(BTNode* root):
⑪int BinaryTreeComplete(BTNode* root):
⑫int maxDepth(struct TreeNode* root):
五·二叉树的oj刷题:
1·对称二叉树:
2·另一棵树的子树:
3·平衡二叉树:
4·翻转二叉树:
一·树的介绍和表示:
首先,要知道树是一种非线性结构,然后第一个是它的根节点,类似于树一样往下面展开。
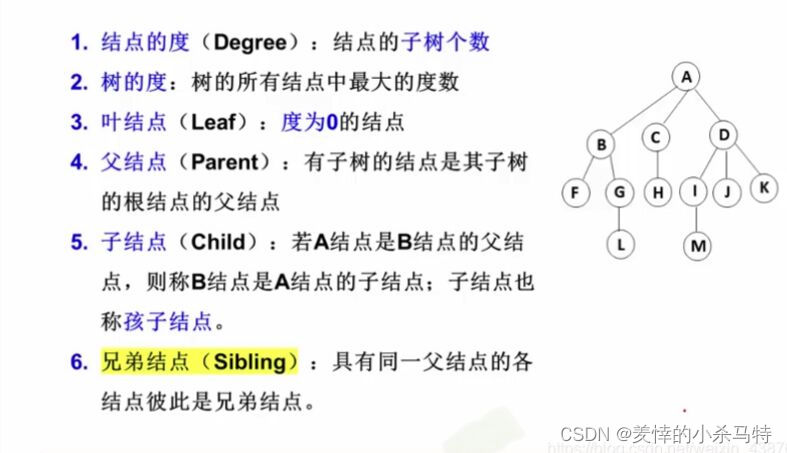
大致长这个样子。
那这样子的树要怎表示呢?
我们用一种叫孩子兄弟表示法:
也就是我们在结构体里面创建的分别为孩子,兄弟,数据这几个项,然后把它们连接起来
typedef int DataType;
struct treenode
{
struct Node* Child;
struct Node* Brother;
DataType data;
};
当然,这种研究起来比较复杂,接下来介绍一下二叉树。
二·二叉树的介绍及性质:
二叉树就是一个根引出两个支,然后延续下去,成为二叉树的左右子树,然后这就给了它一个限制,也就是每个节点只能引出两条边,也就是度最大为2。
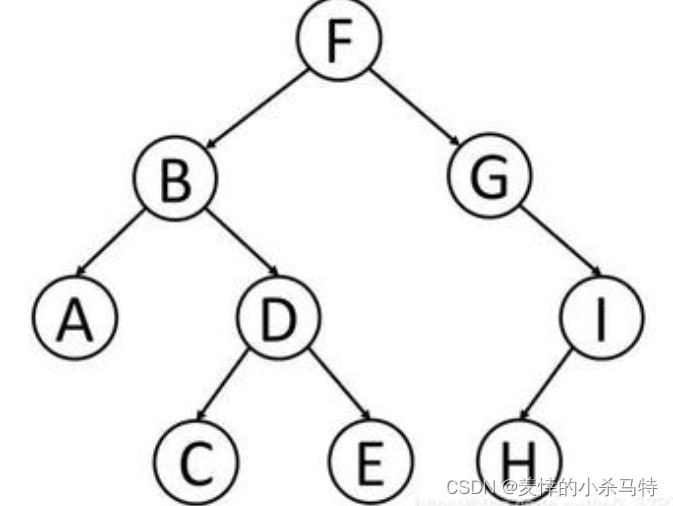
然后二叉树又分为:
1·不完全二叉树:不完全的话就是完全的反面如上面的这棵树就是不完全二叉树。
2·完全二叉树:完全的话就是每一行从左到右应该是持续排列的,即不能左支无而右支有。如:
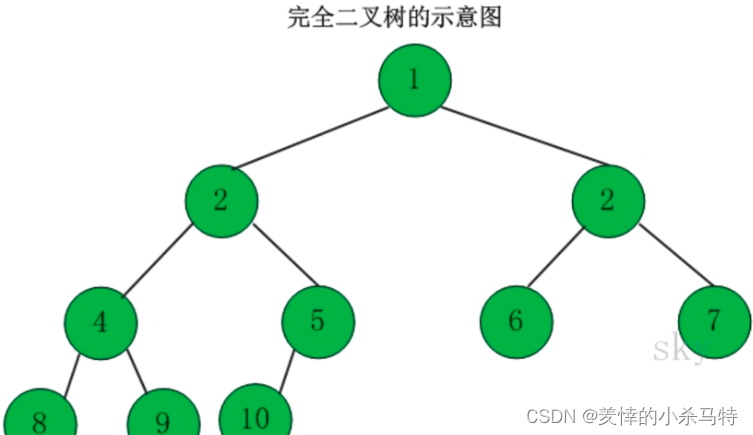
3·满二叉树: 这就是完全二叉树的一种类型,它是每个节点都连接了两个分支,也就是除了叶子层每个节点度都是2.如:

性质:简单说比较重要的就是任何一个二叉树n(度为2)+1=n(度为1) ;下面还有一些性质可做参考:

三·堆的介绍及创建:
堆其实也可以看做一颗完全二叉树,它是非线性结构。然后又可以分为大堆和小堆。
1·小堆:树中父亲节点的值小于或等于孩子节点值。
2·大堆:树中父亲节点的值大于会等于孩子节点的值。
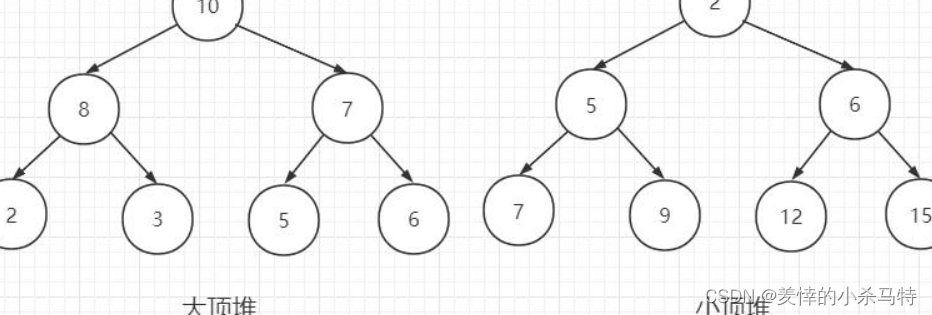
因此我们创建堆可以分这两类。
那这个有什么用途呢?我们可以用它topk(在很多数据中找到前k个数据)以及排序问题。
1·堆的创建:
那么下面我们先来实现一下堆:
首先我们先创建这样的结构体,利用数组来实现。
typedef struct Heap {
int capacity;
int size;
headpdata* a;
}Hp;下面介绍一下,向上调整和向下调整。首先对于堆来说要知道孩子还父亲在数组里对应的关系。
int parent = (child - 1) / 2;
int child = parent * 2 + 1;上调:就是从孩子节点往上调整,也就是如果我们要建立小堆的话,如果孩子比父亲小那么就让两者互换得到新的孩子一直循环下去,直到孩子的下标大于0即完成,大堆变动一下即可。
下调:还是拿小堆为例子,拿到父亲节点值与两个孩子比较,得到两个孩子中最小的交换,再次得到新的父亲节点,再求下一个孩子节点,直到孩子节点到达数组最大长度n终止。
然后这里我们在每一次上调或者下调的时候要确保这个数组构成的堆是有序的。
然后我们每次删除堆顶元素,需要让它和尾部元素交换,然后得到一个除了堆顶元素外剩下都有序的堆然后下调,同理插入的时候,每次插入都进行上调。
下面展示一下堆的代码:
heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int headpdata;
typedef struct Heap {
int capacity;
int size;
headpdata* a;
}Hp;
void Hpinit(Hp* p);//初始化
void Hpdestroy(Hp* p);//销毁
void Hppush(Hp* p, headpdata x);//数据入堆
void Hpupadjust(headpdata* a, int child);//数据在堆中上调
void Hpdownadjust(headpdata* a, int parent, int n);//下调
bool Hpempty(Hp* p);//判空
headpdata Hptop(Hp* p);//返回堆顶元素;
void Hppop(Hp* p);//删除堆顶元素
heap.c
#define _CRT_SECURE_NO_WARNINGS
#include"heap.h"
void swap(headpdata* a, headpdata* b) {
headpdata tmp = *a;
*a = *b;
*b = tmp;
}
void Hpinit(Hp* p) {
assert(p);
p->capacity = p->size = 0;
p->a = NULL;
}
void Hppush(Hp* p, headpdata x) {
assert(p);
if (p->capacity == p->size) {
int newcapacity = p->capacity == 0 ? 4 : 2 * p->capacity;
headpdata* m = (headpdata*)realloc(p->a, sizeof(headpdata) * newcapacity);
if (m != NULL) {
p->a = m;
p->capacity = newcapacity;
}
else {
perror(realloc);
}
}
p->a[p->size] = x;
p->size++;
Hpupadjust(p->a, p->size - 1);
}
void Hpupadjust(headpdata* a, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
//小堆(<)
//大堆(>)
if (a[child] < a[parent]) {
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else {
return;
}
}
}
void Hpdownadjust(headpdata* a, int parent, int n) {
int child = parent * 2 + 1;
while (child < n) {
//假设孩子为左孩子
if (child + 1 < n && a[child] > a[child + 1]) {
child++;
}
//小堆:child>child+1
//此时的child一定是最小的一个
if (a[child] < a[parent]) /*小堆(<)*/
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
return;
}
}
}
bool Hpempty(Hp* p) {
assert(p);
return p->size == 0;
}
headpdata Hptop(Hp* p) {
assert(p);
return p->a[0];
}
void Hppop(Hp* p) {
assert(p);
swap(&p->a[0], &p->a[p->size - 1]);
p->size--;
Hpdownadjust(p->a, 0, p->size);
}
void Hpdestroy(Hp* p) {
assert(p);
free(p->a);
p->a = NULL;
p->capacity = p->size = 0;
}
test.c
#define _CRT_SECURE_NO_WARNINGS
#include"heap.h"
void test1() {
Hp hp;
Hpinit(&hp);
Hppush(&hp, 2);
Hppush(&hp, 11);
Hppush(&hp, 9);
Hppush(&hp, 8);
Hppush(&hp, 5);
Hppush(&hp, 2);
Hppush(&hp, 4);
for (int i = 0; i < 7; i++)
{
printf("%d ", Hptop(&hp));
Hppop(&hp);
}
Hpdestroy(&hp);
}
int main() {
test1();
return 0;
}这样就建好堆了,至于每次上下调传的是数组的指针而不是结构体指针方便下面我们可以直接调用数组进行堆排序。
2·堆的应用:
堆排序:以小堆为例介绍,其实就是我们创建好数组然后给它传递过去,上调的话就是从第一个开始遍历这个数组每次都调用一次上调,最后这个数组就会是一个小堆,接着每次让堆顶元素跟尾部元素交换然后尾指针--;然后对这个堆(由于除了堆顶元素其他都有序,故下调,无论建大堆还是小堆均这样)最后就得到了降序的数组。
然后由于时间复杂度,通常选用下调建堆。
堆排序也通常要记住:升序建大堆,降序建小堆。
代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//数组内部堆排序:
//数组升序则大堆排列,数组降序则小堆排列
//数据往上下调时候,原堆应该是有序的
void swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void Hpupadjust(int* a, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
//小堆(<)
if (a[child] < a[parent]) {
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else {
return;
}
}
}
void Hpdownadjust(int * a, int parent, int n) {
int child = parent * 2 + 1;
//小堆(<)
while (child < n) {
//假设孩子为左孩子
if (child + 1 < n && a[child] > a[child + 1]) {
child++;
}
//大堆child<child+1
if (a[child] <a[parent])/*小堆(<) */{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
return;
}
}
}
/升序大堆,降序小堆
void sort_upadjust(int* a, int n) {
for (int i = 1; i < n; i++) {
Hpupadjust(a, i);//上调
}
/*for (int i = 0; i < n; i++) {
printf("%d ", a[i]);
}
printf("\n");*/
int end = n - 1;
while (end > 0) {
swap(&a[0], &a[end]);
Hpdownadjust(a, 0,end);
end--;
}
for (int i = 0; i < n; i++) {
printf("%d ", a[i]);
}
}
void sort_downadjust(int* a, int n) {
for (int i = (n-2)/2; i >=0; i--) {
Hpdownadjust(a, 0, i);//下调
}
int end = n - 1;
while (end > 0) {
swap(&a[0], &a[end]);
Hpdownadjust(a, 0, end);
end--;
}
for (int i = 0; i < n; i++) {
printf("%d ", a[i]);
}
}
int main() {
int a[] = { 4,6,28,99,34,66,1,1,2,377,4 };
int r=sizeof(a)/sizeof(a[0]);
sort_upadjust(a,r);//上调生成堆的排序
sort_downadjust(a, r);//下调生成堆的排序
return 0;
}还有一个应用就是在大量数据中找出前k个:
这里我们在文件内生成十万个数据模拟一下,然后为了节省空间选择建立一个k个数的小堆(假设k=5);然后把它建成小堆,先从文件中读取5个数建好,然后接下来每次读取一个跟堆顶元素比较比它大就覆盖它重新下调,这样每次我们都能选出6个数中最大的5个并且淘汰一个已知不合要求的数字,然后循环下去得到最终的前五。
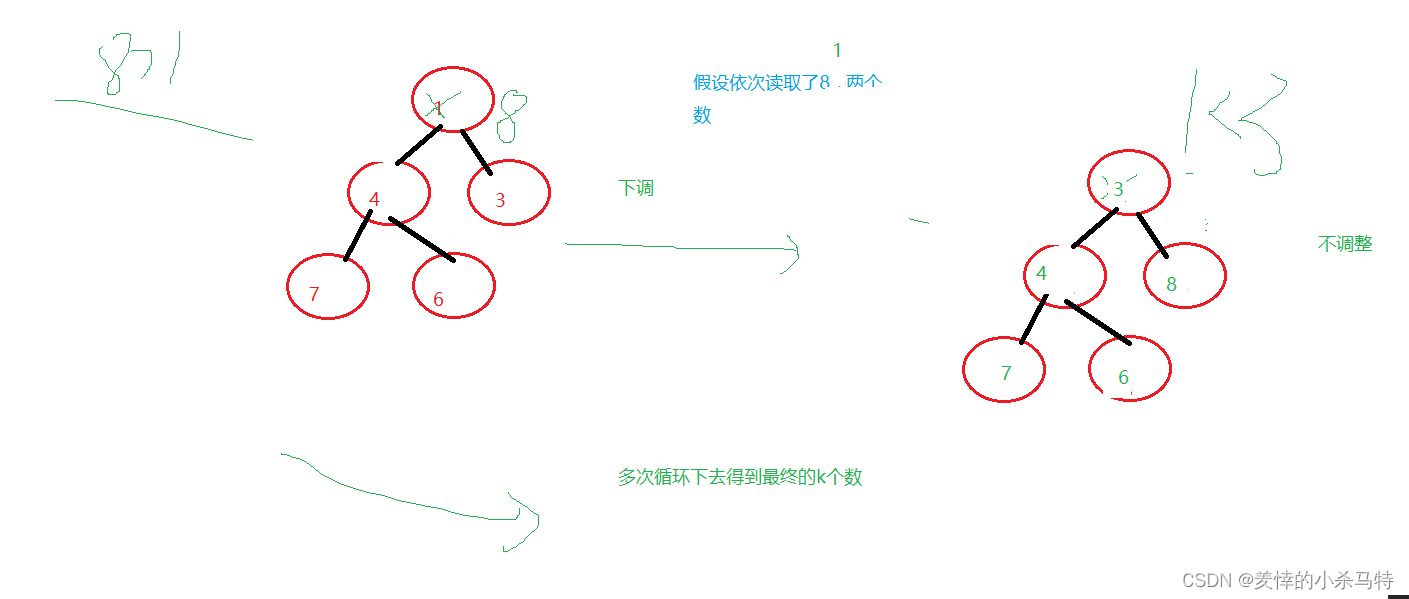
如果我们要得到有序的k个最大的数,可以再调用一下上面的堆排序:
代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<time.h>
#include<stdlib.h>
void swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void Hpdownadjust(int* a, int parent, int n) {
int child = parent * 2 + 1;
//小堆(<)
while (child < n) {
//假设孩子为左孩子
if (child + 1 < n && a[child] > a[child + 1]) {
child++;
}
//大堆child<child+1
if (a[child] < a[parent])/*小堆(<) */ {
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
return;
}
}
}
void createdata() {
FILE* file = fopen("data.txt", "w");
if (file == NULL) {
perror(fopen);
return;
}
int j = 0;
srand((unsigned int)time(NULL));
for (int i = 0; i < 100000; i++) {
j = (rand() + i) % 100000;//srand产生的随机数会有重复,给他+i可以减少重复数据
fprintf(file, "%d\n", j);
}
fclose(file);
}
int main() {
/*createdata();*///创作10w个数据
//读入数组内
printf("请输入要找的最大的前k个数>: ");
int k = 0;
scanf("%d", &k);
int* a = (int*)malloc(sizeof(int) * k);
FILE* fout = fopen("data.txt", "r");
if (fout == NULL) {
perror(fopen);
return;
}
for (int i = 0; i < k; i++) {
fscanf(fout, "%d", &a[i]);
}
/*for (int i = 0; i < k; i++) {
printf("%d ", a[i]);
}*/
//向下调整建立小堆:
for (int i = (k - 2) / 2; i >=0; i--) {
Hpdownadjust(a, i, k);
}
//一个个把剩下的n-k个数据读出来与a[0]比大小,大则替换:
// 可以确保小堆里面的数据一定比替换下去的数据大
//这样就可以一次舍去不合要求数据
int x = 0;
while (fscanf(fout, "%d", &x)!=EOF) {//fscanf输出异常为EOF否则
if (x > a[0]) {
a[0] = x;
Hpdownadjust(a, 0, k);
}
/*printf("%d ", fscanf(fout, "%d", &x));*///返回的为实际读取数据的个数:1
}
fclose(fout);
//逆序输出最大前k个数:
int end = k - 1;
while (end) {
swap(&a[0], &a[end]);
end--;
Hpdownadjust(a, 0, end+1);
}
for (int i = 0; i < k; i++) {
printf("%d ", a[i]);
}
return 0;
}以上就是堆的一些应用。
四·二叉树的创建:
首先创建一个存放字符数据的树,先定义结构体:
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;①// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树BTNode*BinaryTreeCreate(BTDataType* a, int n, int* pi):
这里首先创建一个返回可放入数据的一个节点,然后每次判断只要是#就返回NULL,否则放入数据,然后再左子树右子树走下去,每当判断完或者放完数据就让指针++;然后函数不断调用自己,直到归到返回的最开始的根节点。(由于函数调用自己要想改变下标的值必须传地址用指针接收)
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) {
if (a[*pi] == '#') {
return NULL;
}
BTNode* node = createnode(a[*pi]);
(*pi)++;
node->left = BinaryTreeCreate(a, n, pi);
(*pi)++;
node->right = BinaryTreeCreate(a, n,pi);
return node;
}②void BinaryTreeDestory(BTNode** root):
这里为了销毁的完整选择的是只要不为空左右子树遍历下去,然后当左右子树都为空时,把这个根释放掉。
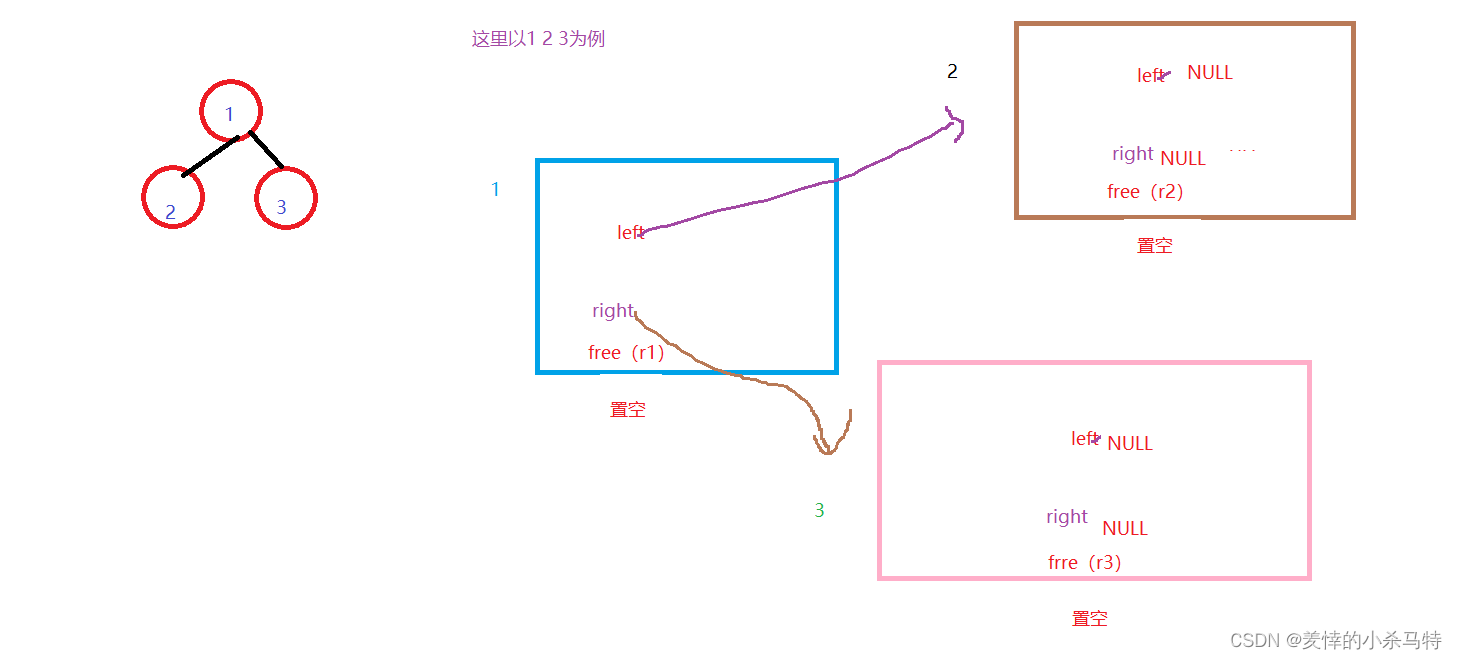
void BinaryTreeDestory(BTNode** root) {
if (*root != NULL) {
BinaryTreeDestory(&((*root)->left));
BinaryTreeDestory(&((*root)->right));
free(*root);
*root=NULL;
}
}
③int BinaryTreeSize(BTNode* root):
就是节点的个数,可以从根(不为NULL)开始左右子树遍历,每遍历一次就加1,故就是1+遍历的左子树+遍历的右子树,为NULL就返回0。
int BinaryTreeSize(BTNode* root) {
if (root == NULL) {
return 0;
}
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}④int BinaryTreeLeafSize(BTNode* root):
首先要知道只有当它的左右子树都为NULL,那么就是叶子,故可以加一,否则在不为空的情况下就递归返回它的左子树加右子树,直到为空就返回0。
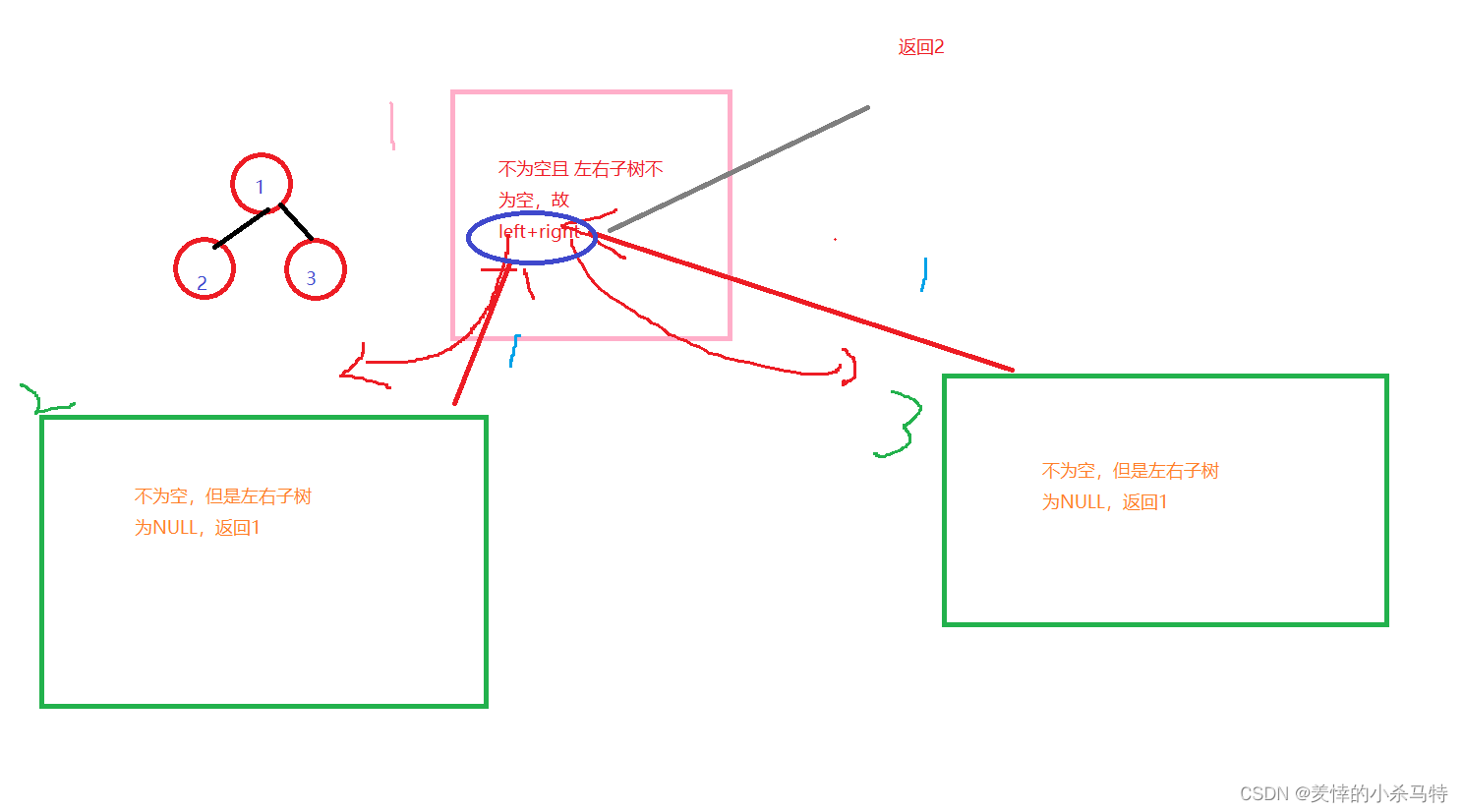
int BinaryTreeLeafSize(BTNode* root) {
if (root == NULL) {
return 0;
}
if (root->left==NULL && root->right == NULL) {
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
⑤int BinaryTreeLevelKSize(BTNode* root, int k):
可以通过每次遍历左右子树就让k的值-1直到达到1,也就是递归的时候这一层就是一开始要找的第k层就返回1。

int BinaryTreeLevelKSize(BTNode* root, int k) {
if (root == NULL) {
return 0;
}
if (k == 1) {
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
⑥BTNode* BinaryTreeFind(BTNode* root, BTDataType x):
法一:这里,可以考虑把它按照层序查找入栈,然后一个个去访问栈中的元素,一旦发现就返回这个指针,到最后也没发现就返回NULL;思路同⑩
代码:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
queue q;
Queueinit(&q);
Queuebackpush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* ret = Queuefrontdata(&q);
Queuefrontpop(&q);
if (ret->data == x) {
Queuedestroy(&q);
return ret;
}
if (ret->left != NULL) {
Queuebackpush(&q, ret->left);
}
if (ret->right != NULL) {
Queuebackpush(&q, ret->right);
}
}
Queuedestroy(&q);
return NULL;
}法二:在前提首根不为NULL情况下遍历它的左右子树,如果发现了x就返回这个根,否则接着
左右子树接着调用找,用指针记录它们的返回值,并保存,等到归回去的时候,如果不为空就把它返回最终得到x所在节点的指针。
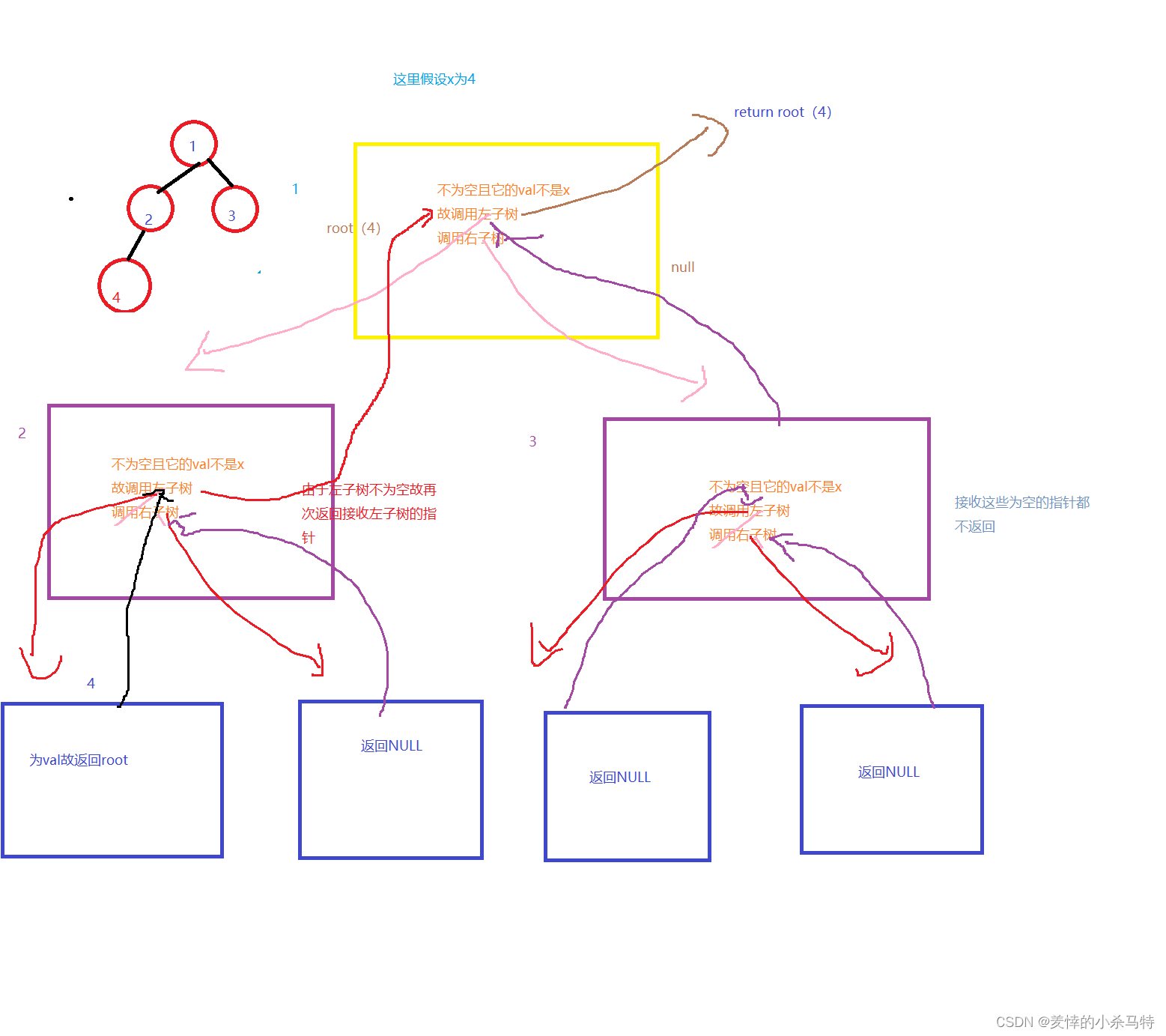
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
if(root==NULL){
return NULL;
if(root->val==x){
return root;
}
BTNode*ret1=BinaryTreeFind(root->left);
if(ret1){
return ret1;}
BTNode*ret2=BinaryTreeFind(root->right);
if(ret2){
return ret2;}
}
⑦void BinaryTreePrevOrder(BTNode* root):
也就是根左右方式去遍历,打印的话就是遇到根就把它打印,然后再分别去遍历左右两支。
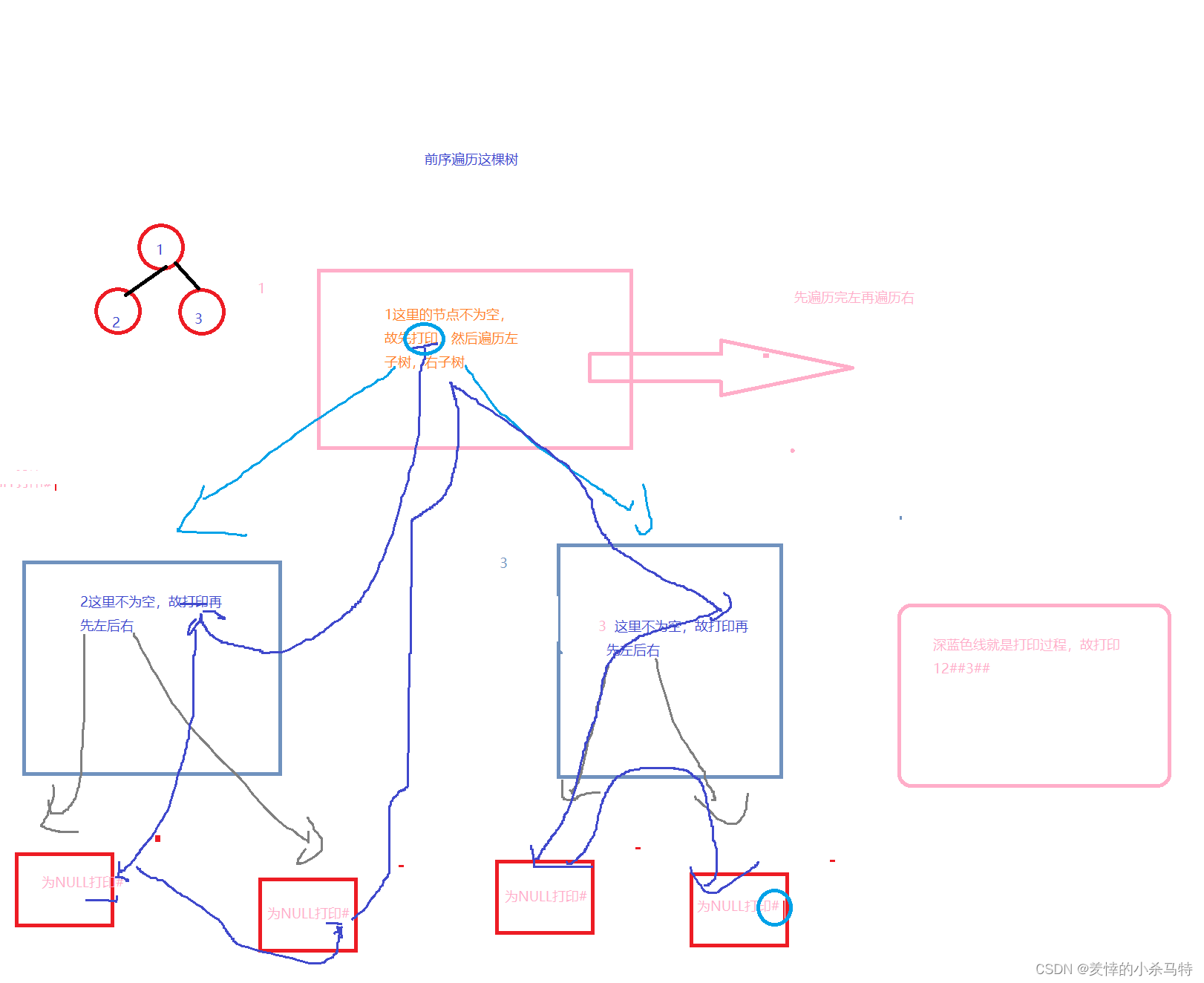
void BinaryTreePrevOrder(BTNode* root) {
if (root == NULL) {
printf("# ");
return;
}
printf("%c ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
⑧void BinaryTreeInOrder(BTNode* root):
也就是左根右方式去遍历,一直遍历左树后打印然后再调用右树。
与前序相类似:
void BinaryTreeInOrder(BTNode* root) {
if (root == NULL) {
printf("# ");
return;
}
BinaryTreeInOrder(root->left);
printf("%c ", root->data);
BinaryTreeInOrder(root->right);
}⑨void BinaryTreePostOrder(BTNode* root):
也就是左右根方式去遍历,一直遍历右树后打印然后再调用左树,与中序打印换一下位置。
void BinaryTreePostOrder(BTNode* root) {
if (root == NULL) {
printf("# ");
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%c ", root->data);
}⑩void BinaryTreeLevelOrder(BTNode* root):
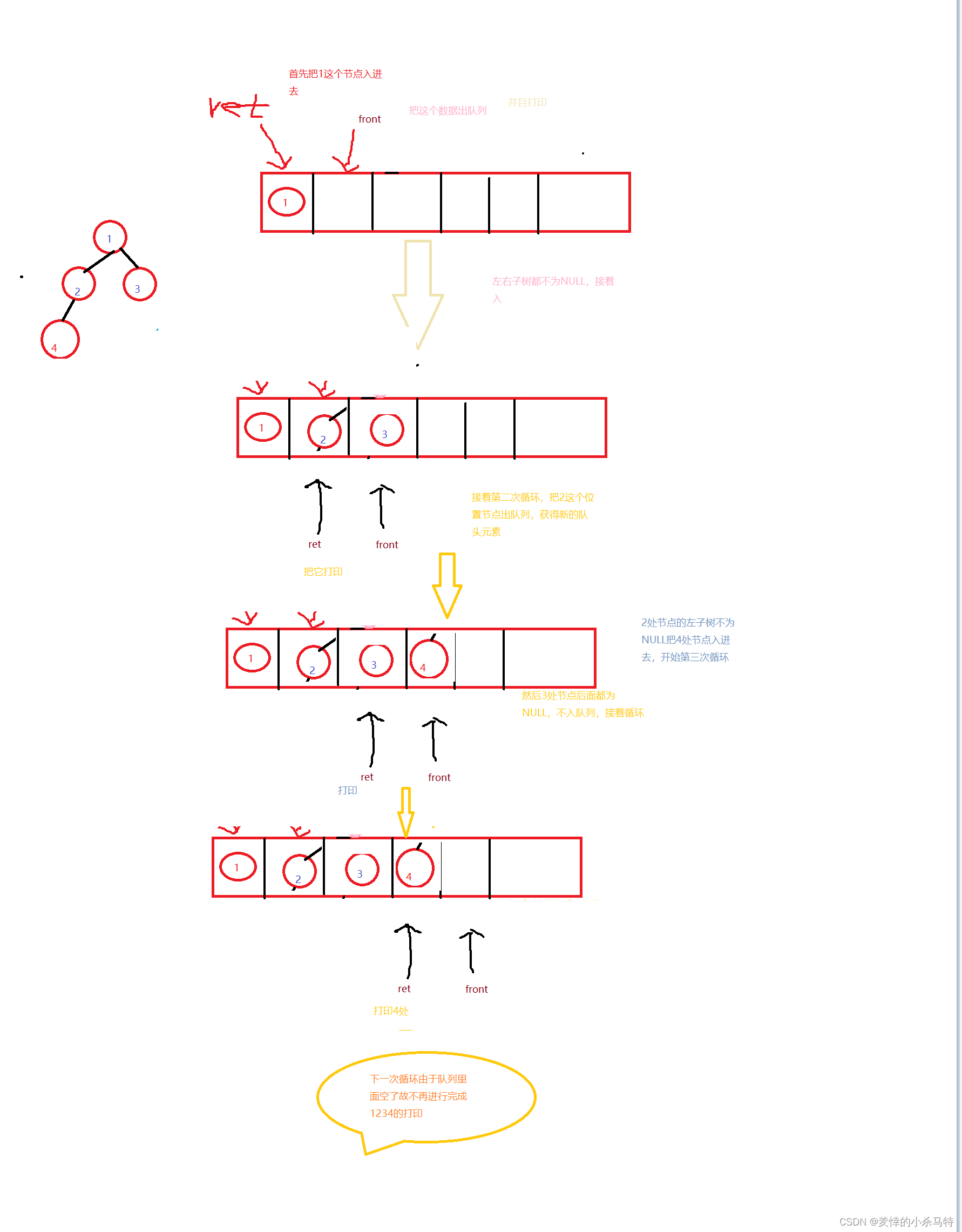
首先建立一个队列然后入队列的数据类型是这个树节点的类型,然后先把树的头根入进去,之后把出队列,然后保存并打印,只要它的左右子树不为空就入进去,循环下去,为空就退,最后就能都打印出。
void BinaryTreeLevelOrder(BTNode* root) {
queue q;
Queueinit(&q);
Queuebackpush(&q, root);
while (!QueueEmpty(&q)) {
BTNode*ret=Queuefrontdata(&q);
Queuefrontpop(&q);
printf("%c ", ret->data);
if (ret->left!= NULL) {
Queuebackpush(&q, ret->left);
}
if (ret->right!= NULL) {
Queuebackpush(&q, ret->right);
}
}
Queuedestroy(&q);
}
这里会不会一个疑问,就是队列为空时候可不可能还有树的节点指针没有进去,然而要知道只要父亲被移除了队列后那么他的孩子一定能进去。
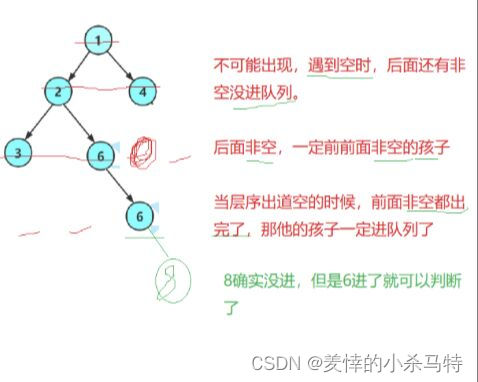
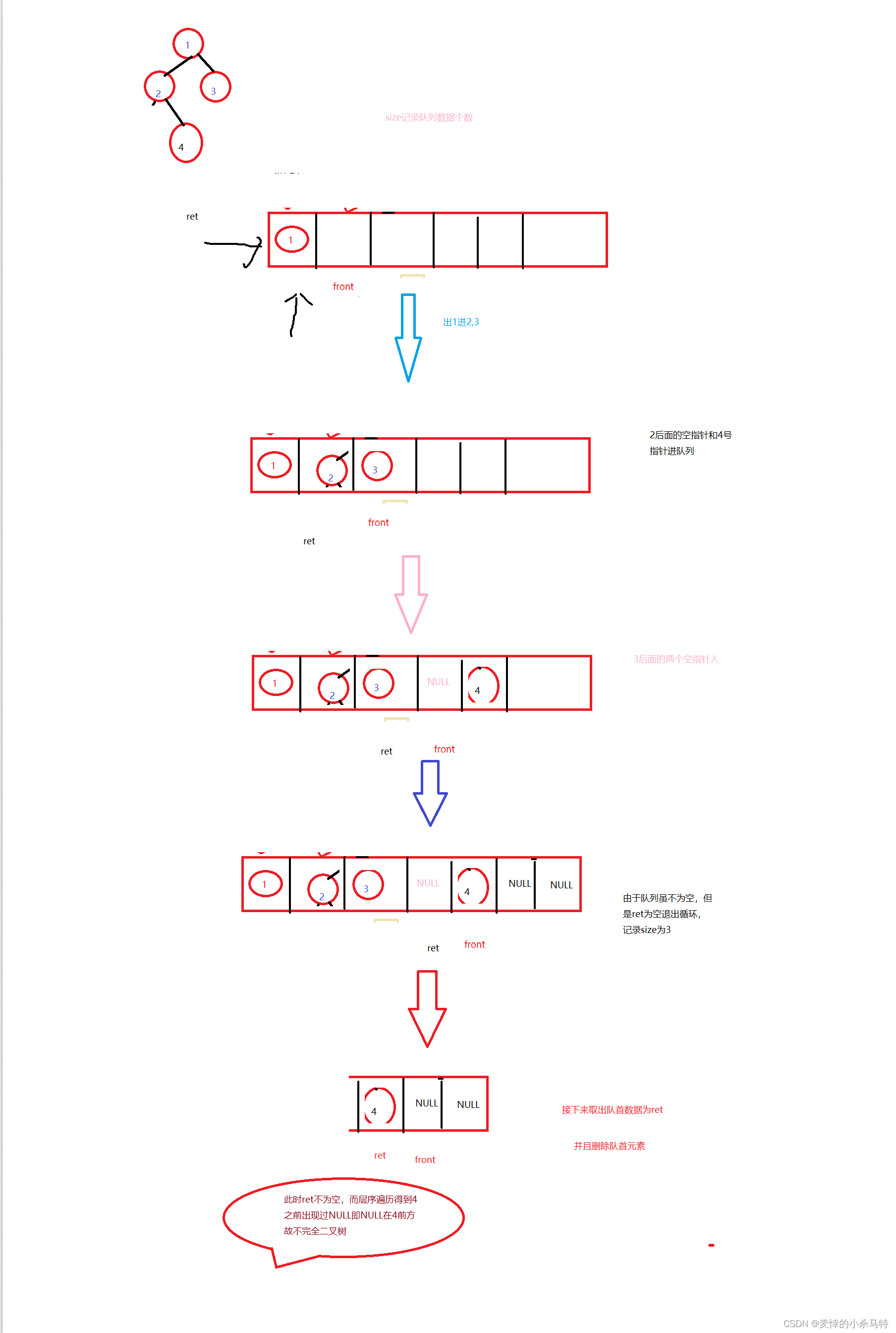
⑪int BinaryTreeComplete(BTNode* root):
还是把它放入队列,然后有进有出,当我们把空节点的指针放进去,那么只要我们在出队列时候读取数据,只要读到了空,就停止,时刻记录队列内数据的个数,然后依次去出队列剩下的数据,如果读到了不是空的指针就证明不是完全二叉树直接返回,如果读到size为0还为读到有数据,即完全二叉树。
int BinaryTreeComplete(BTNode* root) {
int is = 1;
int size = 0;
queue q;
Queueinit(&q);
Queuebackpush(&q, root);
size = 1;
BTNode* ret = NULL;
while (!QueueEmpty(&q)) {
ret = Queuefrontdata(&q);
Queuefrontpop(&q);
size--;
if (ret != NULL) {
Queuebackpush(&q, ret->left);
Queuebackpush(&q, ret->right);
size += 2;
}
else {
break;
}
}
while (size--) {
ret = Queuefrontdata(&q);
Queuefrontpop(&q);
if (ret != NULL) {
is = 0;
break;
}
}
Queuedestroy(&q);
return is;
}
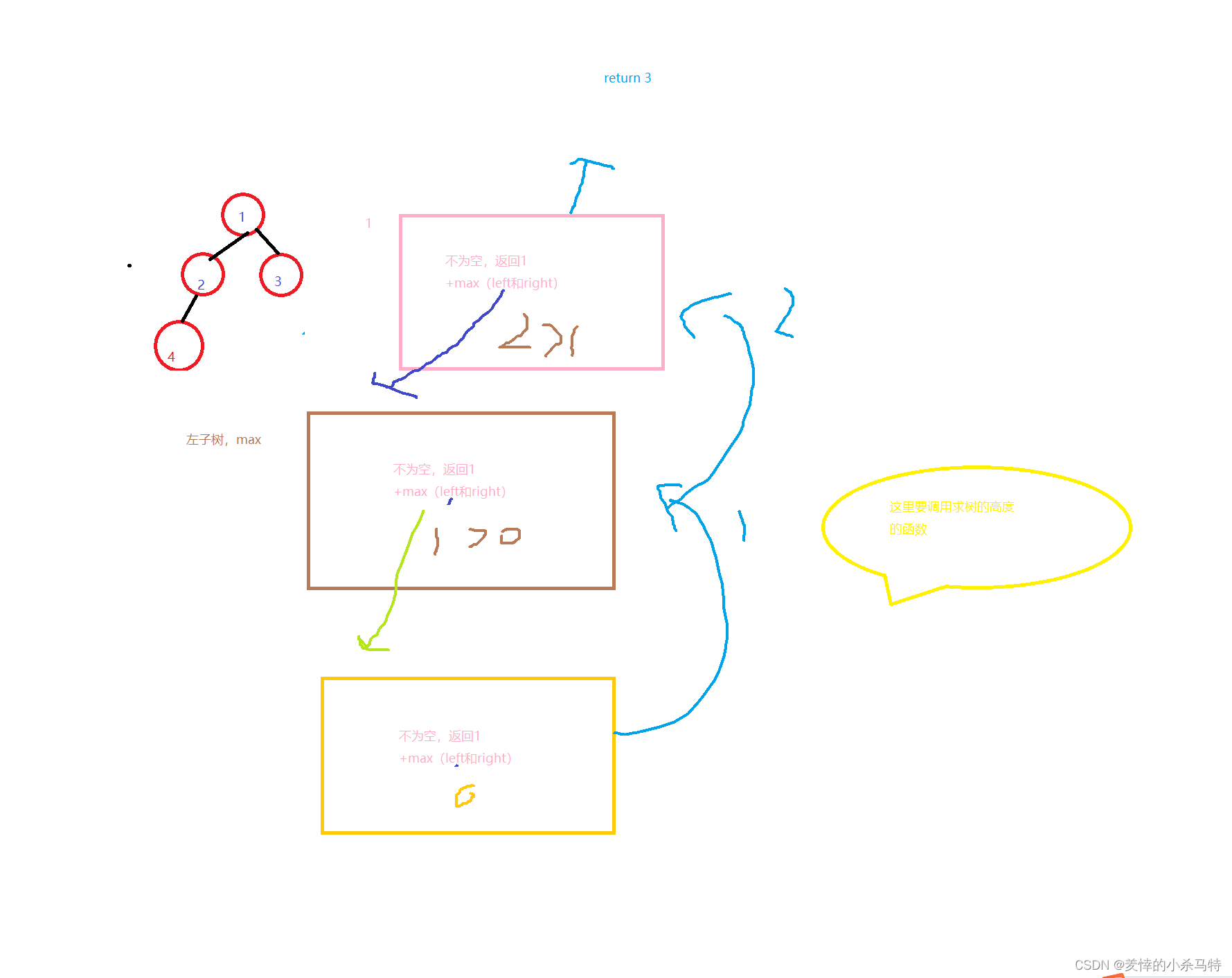
⑫int maxDepth(struct TreeNode* root):
即树的高度,就是1+左右子树最长的树,然后一次递归下去(在前提首根不为NULL情况下)。
注:这里由于多次递归复杂问题,可以把之前递归得到的值保存,在进行比较。
int maxDepth(struct TreeNode* root) {
if (root == NULL) {
return 0;
}
int lefthigh = maxDepth(root->left);
int righthigh = maxDepth(root->right);//这里把计算的子树的深度保存防止下一次再次递归
return lefthigh > righthigh ? (lefthigh + 1) : (righthigh + 1);
}
五·二叉树的oj刷题:
1·对称二叉树:
链接:. - 力扣(LeetCode)
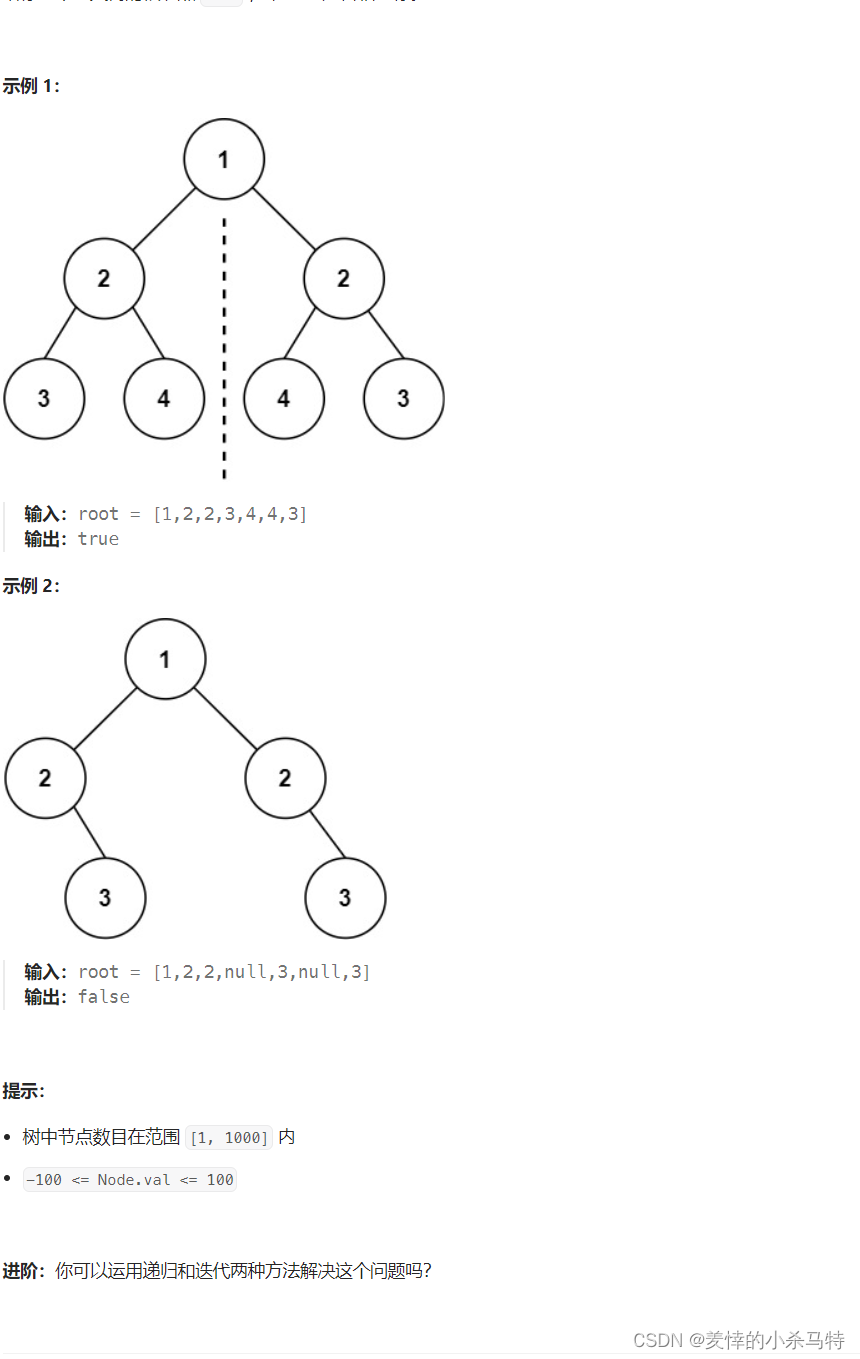
思路:如果数都为null那么肯定不对称,不是null那么就可以类比判断两颗树是否相同,即每次比较左右子树,但是是左子树左支和右子树右支比,左子树右支和右子树左支比,然后递归下去,只有每次判断都是true才成立,用&&
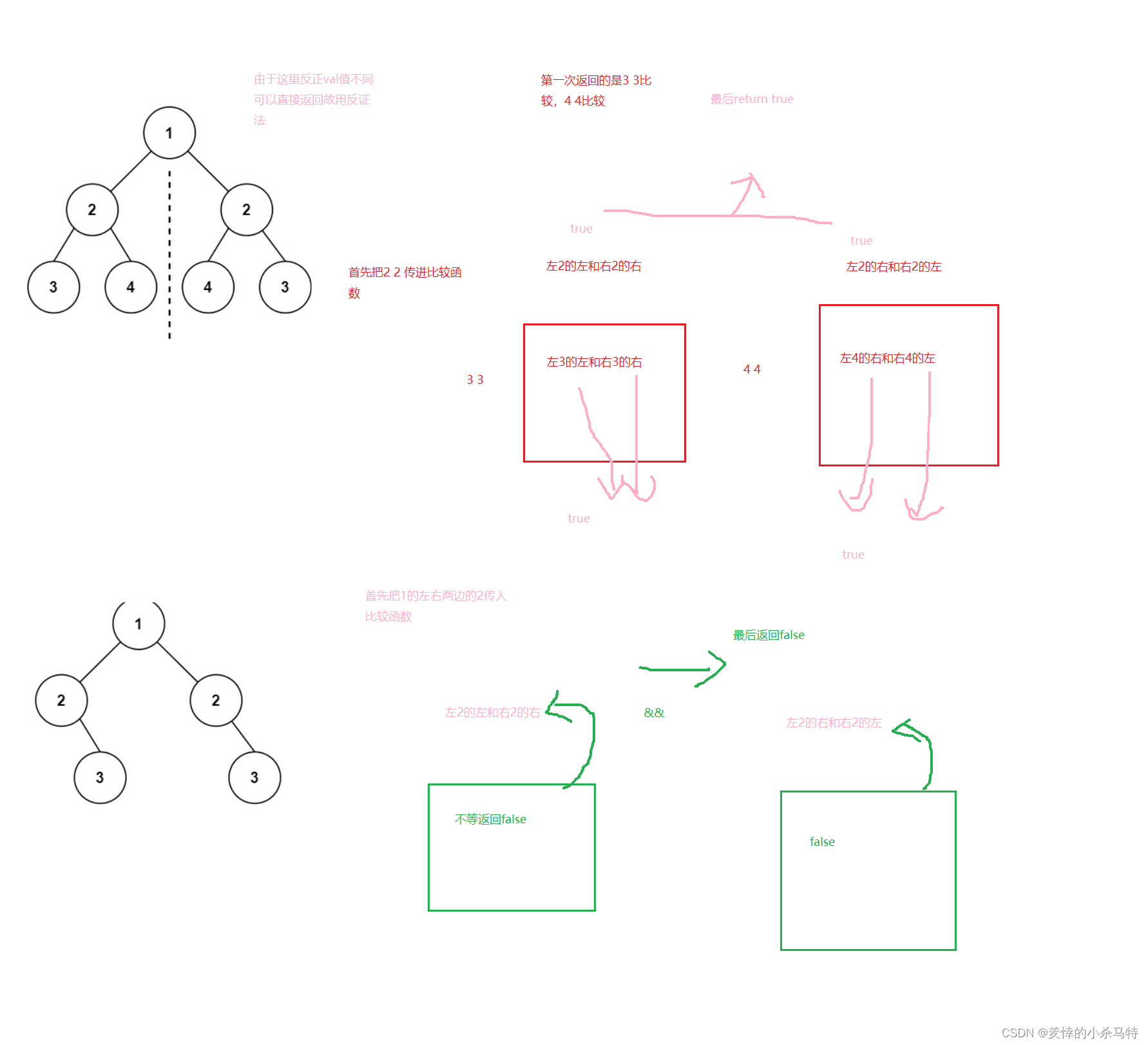
bool issimilar(struct TreeNode* p, struct TreeNode* q){
if(p==NULL&&q==NULL){
return true;//判断位置合适也是终止条件(true)
}
if(p==NULL||q==NULL){
return false;//上面已经判断了q p不可能同时为空,那么其中至少一个为空就false
}
if(q->val!=p->val){
return false;//判断数值是否合适
}
return issimilar( p->left,q->right)&&issimilar( p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) {
if(root==NULL){
return false;
}//判断一开始就不为空
return issimilar( root->left,root->right);
}
2·另一棵树的子树:
链接:. - 力扣(LeetCode)
思路:首先root如果为NULL肯定不成立,如果root不为空,就遍历root这棵树,然后每次可以得到他的一个节点,就调用比较两棵树是否相同的函数,每到root的一个节点就用一下 isSameTree,然后每次调用遍历函数 只要发现了相同就是出现了true即成立,故这里用||

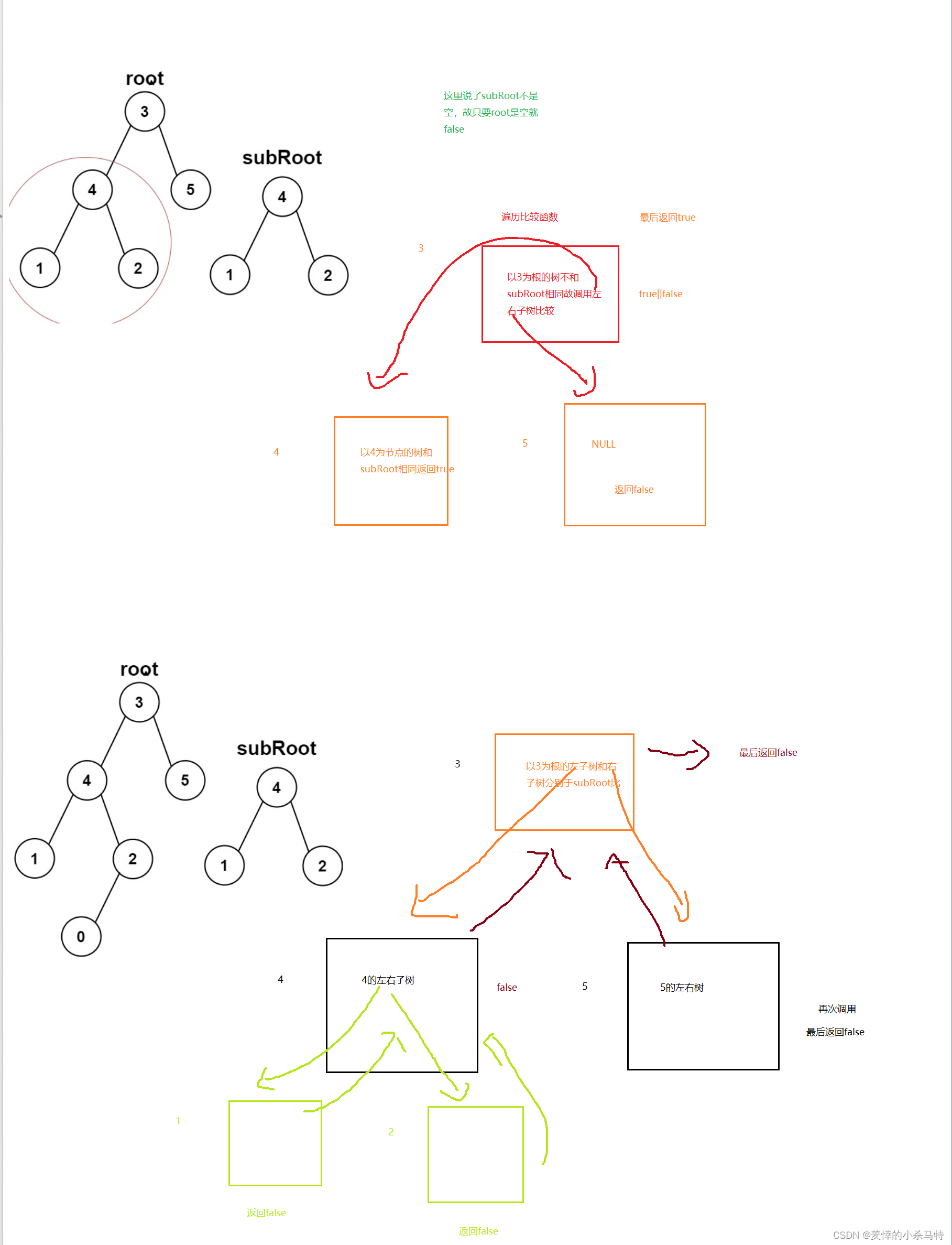
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if(q==NULL&&p==NULL){
return true;//判断位置合适也是终止条件(true)
}
// if(p==NULL&&q!=NULL){
// return false;
// }
// if(p!=NULL&&q==NULL){
// return false;
// }
if(p==NULL||q==NULL){
return false;//上面已经判断了q p不可能同时为空,那么其中至少一个为空就false
}
if(q->val!=p->val){
return false;//判断数值是否合适
}
return isSameTree(p->left,q->left)&& isSameTree(p->right,q->right);//由于为bool类型,只有遍历的两棵树
// 左右都返回的true才能证明完全相等,故yong&&
}
bool prefind_istree(struct TreeNode*p,struct TreeNode*q){
if(p==NULL){
return false;
}
if( isSameTree(p,q)==true){
return true;
}//证明找到子树
return prefind_istree(p->left,q)||prefind_istree(p->right,q);//找到了就可以返回存在一个就可
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root==NULL){
return false;
}
return prefind_istree(root,subRoot);
}
3·平衡二叉树:
链接:. - 力扣(LeetCode)
思路:先建立一个比较树高度的函数,然后让整颗树以及它的左右子树互相比较left与right如果发现小于等于一就返回false否则继续下去直到为空


int maxDepth(struct TreeNode* root) {
if (root == NULL) {
return 0;
}
int lefthigh = maxDepth(root->left);
int righthigh = maxDepth(root->right);//这里把计算的子树的深度保存防止下一次再次递归
return lefthigh > righthigh ? (lefthigh + 1) : (righthigh + 1);
}
bool isBalanced(struct TreeNode* root) {
if(root==NULL){
return true;
}//只能判断首个根是否为NULL
if(abs(maxDepth(root->left)-maxDepth(root->right))>1){
return false;//这里判断>1好写一些
}
return isBalanced(root->left)&&isBalanced(root->right);
}
4·翻转二叉树:
链接:. - 力扣(LeetCode)
思路:依次交换树的左右两支,不断递归直到得到的为叶子,然后用本次递归调用函数的root->左右交换,最后返回的root就是第一次调用函数的root。


struct TreeNode* invertTree(struct TreeNode* root) {
if(root==NULL){
return NULL;
}
struct TreeNode*ret1=invertTree(root->left);
struct TreeNode*ret2=invertTree(root->right);
root->right=ret1;
root->left=ret2;
return root;
}
☺剧终☺