一、不同组织结构类型对组织的沟通效率会带来影响,这也是在组织结构设计过
程需要考虑的重要内容,但对于两者的关系无法准确界定。如在直线职能制的组织结构中,管理幅度和深度是影响是影响沟通效率的主要因素。请设计实验来验证分析直线职能制组织结构中管理幅度和深度对组织沟通效率的影响。
二、在群决策过程中,希望通过整合多方面、多领域的意见和想法,从而实现决
策的科学性和合理性。但是,领域内的专家意见或者领导意见往往会左右决策参与者的判断,从而采取服从专家或领导的意见,这样反而造成失去群决策的初衷,决策效果并不理想。当然,这也与群决策参与者的个性有关。请设计实验来验证分析权威意见在群决策中的影响机制及其作用。
实验设计,应至少包括:
1、实验设计的依据:
2、实验目的:
3、实验变量选取;
4、实验假设;
5、实验设计,如被试选择与分组、实验环境、实验任务、实验收益计算等;
6、实验说明书(用于发放给不同组别或角色的实验指导书)。
ps.信管专业的限选课,工商管理也可以选。听了一次课,讲变量和因变量的。结课作业很操蛋,把这次的作业分享出来,希望帮到误选这门课的同学,苦劝一句,避开地大和大衣,一学分的课,事可不是一学分,不值得。
能否过关?应该是能的,上次的小组作业,流程也和我这次做的差不多,84,这次的结课作业我还画了图,做了下数据分析。
为什么分享?作业已经过了截至时间,不怕抄袭。清理电脑,wps没空间了。
实际上,有些实验的设计可以更合理些,但我没那个心思,我觉得没有意义。
chatgpt是个好东西,润色文章很有一手……凑字数用
中国地质大学(北京)
结课作业
课程名称:管理学实验的设计与实践
任课教师:何大义
学生:符义 1007191127
班级:10071982 信管二班
2023年 1 月
实验一
- 情景假设:
就直线职能制而言,它主要关注于组织中的行政层级结构,以及相应的管理权限等级。本文旨在研究直线职能制中管理幅度和深度对组织沟通效率的影响。管理幅度指的是每一个管理者管理的员工/部门的数量,而深度则指的是每一个管理者的管理权限。本研究将探讨直线职能制中管理幅度和深度的影响以及它们对组织沟通的影响程度。
为探究管理幅度对组织结构的影响,情景设置一维四列矩阵,

假设A可为组织提供管理指导,
1.当A仅指导一列,该列可增加0.3沟通效率,其余部门沟通效率不变;
2.当A指导两列,每列增加0.25效率,其余部门沟通效率不变;
3.当A指导三列,每列增加0.1效率,其余部门沟通效率不变;
4.当A指导四列,每列增加-0.1效率;
变量设置为A的管理幅度。
幅度为一:仅可指导一列;
幅度为二:可指导一或者二列;
幅度为三:可指导一,二,或三列;
幅度为四:可指导一,二,三或者四列;
2.实验过程:
实验依据,某次幅度下确定指导多少列,我们用C++语言中STL库中的rand()函数确定,rand()函数是 C++ 中一种随机数生成函数,它通过使用伪随机算法来生成指定范围内的伪随机数。它可以让我们创建真正随机的程序,而不受计算机硬件的限制,从而更好地模拟真实世界的随机行为。每个幅度用程序运行十次后,计算每次该幅度下总的沟通效率,与对照组进行对比(对照组每列原沟通效率为0.65,总沟通效率为2.6,十次总的为26)后得出结论,目的是确定管理幅度对组织沟通效率的影响。
从研究角度来看,探究深度和宽度是有区别的。深度探究可以加深对问题的理解,提高细节性的分析能力,从而更好地完成组织沟通效率的实验。而宽度探究可以更广泛的视野去观察问题,找出一般化的解决方案和相关的背景,从而为组织沟通带来更高的效率,但本次实验中在探究深度对沟通效率影响,发现可将矩阵转置为和探究管理幅度一样的一维四列矩阵,因此本次的探究管理幅度的结论是可以作用于管理深度的。
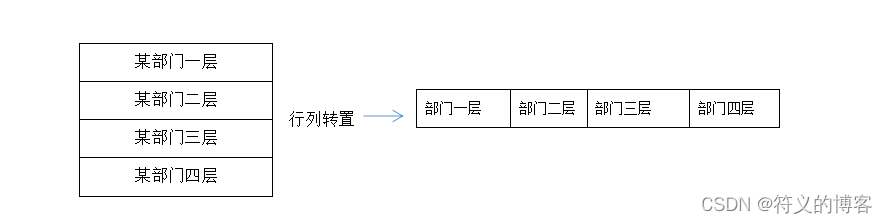
实验可完成对管理幅度对组织沟通效率的实验,而且通过矩阵转置发现探究管理深度和探究宽度的等同性,因此本次实验能评估管理幅度和深度对组织沟通效率的影响,能达成这一目标。
程序运行结果一:

选取某次数据:
管理幅度为1下的十次沟通效率:2.795 2.795 2.795 2.795 2.795 2.795 2.795 2.795 2.795 2.795
该幅度下沟通效率总和:27.950
管理幅度为2下的十次沟通效率:2.925 2.925 2.795 2.925 2.795 2.795 2.925 2.795 2.925 2.795
该幅度下沟通效率总和:28.600
管理幅度为3下的十次沟通效率:2.795 2.795 2.795 2.795 2.795 2.925 2.925 2.795 2.795 2.795
该幅度下沟通效率总和:28.210
管理幅度为4下的十次沟通效率:2.340 2.925 2.795 2.795 2.925 2.340 2.795 2.795 2.925 2.340
该幅度下沟通效率总和:26.975
将其可视化:
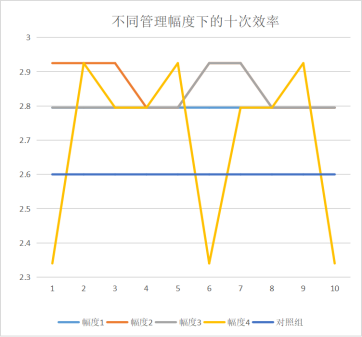
从图上可以看出,随着幅度的增加,沟通效率也呈现出起伏不定的趋势,这可能会影响组织管理的有效性。而从数据来看,A在幅度二,三下的使得组织沟通效率最高,因此,推荐使用幅度二以及幅度三来进行沟通,以此来达到最大的沟通效率。
3.结论与总结:
一、从分析的角度看,在直线职能制的组织架构中,管理幅度和深度都必须在一个合理范围内,这样才能使沟通效率达到较佳水平。如果管理幅度和深度太小,或者太大,都会影响沟通效率,这也是提升沟通效率的一项关键。只有在一个适宜的范围内,才能保证组织的运作效率高,从而推动组织发展和持续增长。
二、不宜将管理幅度或深度扩大到极端情况,虽然可能会使的沟通效率增加,但这样却无法真正避免极端情况的发生,因为最后容易出现不利的结果,包括耗费较多的时间和财力、效率减弱、组织实力受到削弱等。因此,一定要把握好管理幅度和深度,确保比较有效的对应,以最大限度的保护组织或企业的利益,发挥组织的最大功能。
实验一编程代码:
实验一编程代码:
#include<bits/stdc++.h>
using namespace std;
vector<vector<double>> organisation(4,vector<double>(11,0));
//根据输入的参数( i )来计算沟通收益。它从1-4之间进行比较,根据不同的输入来计算不同收益值。
double profit(int i){ //返回沟通效率
if(i==0) return 3*0.65+(0.3+1)*0.65;
else if(i==1) return 2*0.65+(0.25+1)*0.65*2.0;
else if(i==2) return 1*0.65+(0.1+1)*0.65*3;
else return 4*0.65*(1-0.1);
}
int cnt=0;
double fund(int f){
//更新随机数种子
int jk=rand()%f;
cout<<cnt++<<" "<<jk<<" "<<endl;
if(cnt==10) cout<<"ka kaka ";
return profit(jk); // f幅度下,随机选择 指导1~f范围列数
}
int main(){
/*这段代码的作用是通过产生随机数,计算不同管理幅度下10次沟通的效率,并输出每次沟通效率和总效率。*/
srand((unsigned)time(NULL));
for(int i=0;i<4;i++){
double sum=0;
for(int j=0;j<10;j++){
int f=rand()%(i+1);
organisation[i][j]=profit(f);
sum+=organisation[i][j];
}
organisation[i][10]=sum;
}
for(int i=0;i<4;i++){
cout<<"管理幅度为"<<i+1<<"下的十次沟通效率:";
for(int j=0;j<10;j++){
printf("%5.3f ",organisation[i][j]);
}
cout<<"该幅度下沟通效率总和:";
printf("%5.3f ",organisation[i][10]);
cout<<endl;
}
return 0;
}实验二
- 情景假设:
不同影响力对决策收益的影响取决于许多因素,比如已有信息、团队氛围和决策中的风险意识等。这些因素帮助决策者理清思路,从而在最终决策中实现收益最大化。此次实验中仅探究专家或领导的权威影响力对团里决策的收益。
此次实验中记某权威专家为A,将A的权威影响力设置为变量。
我们将团队每个人的决策的收益记为0.7,共有6人,总的收益为4.2,并将其设置为对照组。
由于A为专家,若专家意见被采纳(是否采纳依然用概率模拟),则假设对决策引导有0.55的概率为正向作用,有0.45概率为负作用,正向作用为每团体成员的决策收益,增加0.15;负作用为增加-0.15的团体成员收益。
当A的影响力设置为1~10,值越高,影响团体个人的概率越大,即团体成员采纳专家意见的概率。例如10,则有百分百的机率影响团队成员,影响力为9则有9/10的概率影响团体成员。
为了便于实验编程,将专家的引导作用与影响力关系简化,影响力(影响力即为权威值)若为8~10,若为正向作用,可将团体成员的正向收益额外增加0.05;影响力为1~3,副作用加强,额外增加-0.05。

2.实验过程:
为了更加真实地模拟实验编程,我们需要有一位团体成员来免受专家影响,即该成员不再受到专家影响,而是完全独立决策。且为了使模拟效果更能够达到题意,我们将其收益恒定为0.7。再来,我们需要进行两个步骤:首先,我们需要明确模拟的正确方法,以便它能够准确反映出问题所要求的真实情况;其次,我们需要确定合适的数据结构,来代表每个团队成员,以使计算机系统能够有效对给定的情境和每位成员的决策进行处理。
使用C++ STL库中的rand()函数处理概率问题具有多方面的好处。它有助于更清楚地了解选择的可能结果,并帮助做出合乎真实环境的决定。此外,这个函数能够生成精确的随机数,帮助测量并分析可能的正确性和准确性。也就是说,使用rand()函数可以得到更准确的结果,而不会对结果造成任何影响。因此,要想正确处理概率问题,应该使用C++ STL库中的rand()函数,以提高准确度,它能够在多种形式中产生真正的随机数,而不受外部任何因素的影响。
我们可以在实验编程模拟中增加一些其他的参数,根据不同的参数,可以采用适当的数据结构来实现对团体成员决策的不受干扰,并且可以测试不同的概率分布在解决此问题上的效果。另外,由于使用了随机化的数字算法rand()来构建更为灵活的模拟,从而模拟出不同的情况,使得结论具有更好的精确度。
为了提高数据一致性和可靠性,我们将程序运行多次次,运行结果为不同管理幅度参数下其对应的十次决策收益,并将每个幅度下10轮的收益总和记录下来。最后将结果与对照组比较以得出实验结论。
程序某次运行结果:

将程序运行6次,记录下“决策总收益”:

将数据从列的角度分析,可知影响力在1~3情况下,由于负作用的增强会加大总收益的减少;4~7的收益与对照组持平,影响力在8~10情况下,收益普遍大于对照组。
将数据可视化:
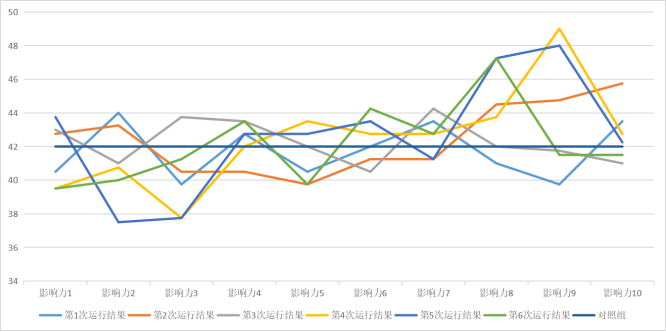
观察上图可知,在影响力处于1~3、8~9的情况下,差值很大,而且数值也分布得比较散。权威值为4~7的情况下,相比对照组,决策效果的影响较小。倘若专家或领导的权威较高,很明显能影响决策效益,作用为正向;若是专家权威较低,虽然在情景设置里已将权威值低的专家,让团体成员将接受其意见的概率降低,但还是发挥了很大负作用。通过剔除极值,研究发现,在团体内部,当权威者影响力增加时,团体决策的收益也会呈上升趋势。
3.结论与总结:
一,权威意见,在给出者具有较大的权威时,亦或较小的权威均能影响到团体决策收益,权威影响力高的专家能使团体决策收益增加。
二,权威值低的专家,即使可信度低,采取其意见的概率小,但是在大样本的情况下依然会有不可忽视的负作用。
三,权威值处于中间范围的专家,在对团体决策的影响是较平缓的,很少会有极端情况,趋向团体决策的收益。
四,伴随着权威度的提高,集体决策的效益也不断增加。
总的来说,权威对群策有很大的关联。权威可以帮助团体达到更高的整体表现,并促进更有效的决策制定,并且从社会学的角度看,权威意见对于团体决策也是十分重要的。高权威值的专家可以增加团体决策的收益,而中间范围的专家则会使团体决策的收益更加平稳。
实验二编程代码:
#include<bits/stdc++.h>
using namespace std;
vector<vector<double>> sd(10,vector<double>(11,0));
bool to_cnt(int i){ //这个函数使用了随机数,采纳专家意见的概率取决于影响参数i,如果t<=i,则返回true,否则返回false,表示不采纳专家意见。
int t=rand()%10+1;
if(t<=i){ //采纳概率为 i/10;
return true;
}else{
return false;
}
}
//上面这段代码的作用是根据一个随机产生的数字来决定是正向作用,还是副作用,其中正//向作用有 55% 的概率,而负作用有 45% 的概率。
bool to_fx(){ //确定是正向作用,还是副作用
int t=rand()%100+1;
if(t<=55) return true;//正向作用 0.55 概率
else return false; //负作用 0.45 概率
}
//代码的作用是根据参数t和i的值,来计算并返回一个双精度浮点数。如果参数t为真,则考虑参数i的值,进行正向或负向计算,最终返回一个计算结果。如果参数t为假,则不考虑参数i的值,仍然返回4.2。
double to_da(bool t,int i){ //参数 是否采纳,影响力
if(t){
if(to_fx()){ //正向作用
double temp= 4.2+5*0.15;
if(i>=8) temp+=5*0.05;
return temp;
}else{ // 负作用
double temp= 4.2+5*(-0.15);
if(i<=3) temp-=5*0.05;
return temp;
}
}else{
return 4.2;
}
}
int main(){
/*这段代码的作用是计算每个影响力下的10轮决策收益,并输出每轮决策的收益以及每个影响力下的总收益。*/
srand((unsigned)time(NULL)); //更新随机 数种子
for(int i=1;i<=10;i++){
double sum=0;
for(int j=0;j<10;j++){
double box=to_da(to_fx(),i);
sum+=box;
sd[i-1][j]=box;
}
sd[i-1][10]=sum;
}
for(int i=0;i<10;i++){
printf("专家影响力为%2.d下,10轮决策收益:",i+1);
for(int j=0;j<10;j++){
printf("%1.2f ",sd[i][j]);
}
cout<<endl;
}
cout<<"每个影响力下的决策总收益"<<endl;
for(int i=0;i<10;i++){
printf("%2.2f ",sd[i][10]);
}
return 0;
}