二叉树——进阶（递归创建，非递归，广度优先，翻转，深度，对称）

二叉树——进阶

二叉树的递归创建
非递归前中后序遍历
- 非递归前序遍历
- 非递归中序遍历
- 非递归后序遍历
广度优先遍历二叉树（层序遍历）
- 翻转二叉树
二叉树深度
- 最大深度
- 最小深度
对称二叉树

二叉树的递归创建

1，二叉树是一种结构相对固定的数据，分为根，左节点，右节点，把一颗大树拆分开每部分都是如此，这就有了递归创建的条件。

2，采用递归，第一时间需要思考递归的三步骤。

基本情况（Base Case）：定义递归算法终止的条件。在递归的过程中，需要确定一个或多个基本情况，当满足这些情况时，递归将停止并返回结果，避免进入无限递归的循环。
递归调用（Recursive Call）：在算法的定义中，通过调用自身来解决问题的步骤。递归调用必须逐渐朝着基本情况靠近，以确保算法能够最终终止。
向基本情况靠近（Making Progress Towards Base Case）：确保递归调用的每一步都朝着基本情况的方向迈进。这意味着在每次递归调用中，问题的规模都会减小，最终达到一个基本情况。

3，这里采用先序创建二叉树，思考递归的终止条件，显而易见，就是遇见空节点时，数据采用整数，每层需要自己输入，还需要返回值，返回根节点。

代码实现：

typedef struct Binary_Tree
{
	DataType val;

	struct Binary_Tree* left;
	struct Binary_Tree* right;

	struct Binary_Tree() {}
	struct Binary_Tree(int v)
	{
		val = v;
		left = NULL;
		right = NULL;
	}
}TreeNode;

//递归先序创建树
TreeNode* create_Tree()
{
	int x;
	cin >> x;

	if (x == -1)  //终止条件
	{
		return NULL;
	}
	
	//数据处理，单层的逻辑执行
	TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
	if (root == NULL)
		exit(-1);

	root->val = x;
	
	//递归创建左右树
	root->left = create_Tree();
	root->right = create_Tree();
	
	//返回结果
	return root;
}

非递归前中后序遍历

1，非递归遍历树，需要用到数据结构——栈来模拟递归时的过程，并且更加复杂一些，需要判断循环终止条件，循环中对树节点的处理，需要多种数据辅助。

非递归前序遍历

非递归先序遍历二叉树的要点通常包括以下几个步骤：

1，使用栈数据结构：在非递归算法中，通常会使用栈来模拟递归调用的过程。栈用于存储待访问的节点，以便稍后访问它们的子节点。

2，遍历顺序：先序遍历的顺序是先访问根节点，然后递归地访问左子树和右子树。因此，在非递归算法中，首先将根节点入栈。

3，迭代过程：

弹出栈顶元素，访问该节点。
将该节点的右子节点（如果存在）入栈，然后将左子节点（如果存在）入栈。注意要先将右子节点入栈，再将左子节点入栈，以保证左子节点在栈中靠近栈顶，右子节点在栈中靠近栈底，这样才能保证先访问左子树。
重复以上步骤，直到栈为空。

4，循环条件：在循环中，应该判断栈是否为空，以确定是否继续遍历。当栈为空时，表示已经遍历完整棵树。

代码实现：

//非递归先序遍历
void non_recursion_PreorderTree(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	//栈结构
	stack<TreeNode*> Tree;

	Tree.push(root);

	while (!Tree.empty())
	{
		TreeNode* tem = Tree.top();

		cout << tem->val << " ";
		Tree.pop();

		if (tem->right != NULL)
			Tree.push(tem->right);

		if (tem->left != NULL)
			Tree.push(tem->left);
	}
}

非递归中序遍历

非递归中序遍历二叉树的要点包括以下几个步骤：

1，使用栈数据结构：与先序遍历类似，在非递归算法中也会使用栈来模拟递归调用的过程。栈用于存储待访问的节点，以便稍后访问它们的子节点。

2，遍历顺序：中序遍历的顺序是先访问左子树，然后访问根节点，最后访问右子树。因此，在非递归算法中，首先将根节点入栈，并将当前节点指向根节点的左子节点。

3，迭代过程：

将当前节点的所有左子节点入栈，直到没有左子节点为止。
弹出栈顶元素，访问该节点。
将当前节点指向该节点的右子节点。
重复以上步骤，直到栈为空且当前节点为空。

4，循环条件：在循环中，应该判断栈是否为空或当前节点是否为空，以确定是否继续遍历。当栈为空且当前节点为空时，表示已经遍历完整棵树。

代码实现：

//非递归中序遍历
void non_recursion_MidorderTree(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	stack<TreeNode*> Tree;
	TreeNode* cur = root;
	Tree.push(cur);
	while (!Tree.empty() || cur)
	{
		if (cur && cur->left != NULL)
		{
			Tree.push(cur->left);
			cur = cur->left;
		}
		else
		{
			cur = Tree.top();
			cout << cur->val << " ";
			Tree.pop();
			if (cur->right)
			{
				Tree.push(cur->right);
			}
			cur = cur->right;
		}
	}
}

非递归后序遍历

非递归后序遍历二叉树的要点包括以下几个步骤：

1，首先，检查根节点是否为空。如果为空，则直接返回，因为空树无需遍历。

2，创建一个栈 s 用于存储待访问的节点。

3，初始化当前节点 cur 和前一个访问过的节点 pre 为根节点 root。

4，进入循环，条件是当前节点不为空或者栈不为空。这保证了遍历能够进行到所有节点都被访问过为止。

5，在循环中，首先进行左子树的遍历。从根节点开始，将当前节点和其所有左子节点依次入栈，直到当前节点为空。

6，接着，检查栈顶元素（即当前节点）的右子树情况。如果右子树存在且未被访问过，则将当前节点指向右子节点，并重新进入左子树遍历的步骤。

7，如果当前节点的右子树为空或者已经被访问过，则说明当前节点是可以访问的。输出当前节点的值，并将当前节点标记为上一个访问过的节点 pre，然后将当前节点设为 NULL，表示已经访问过。最后，将当前节点出栈。

8，重复步骤 4 到步骤 7，直到栈为空，表示所有节点都已经遍历完成。

代码实现：

//非递归后序遍历
void non_recursion_rearorderTree(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	TreeNode* cur = root;
	TreeNode* pre = root;
	stack<TreeNode*> s;
	while (cur || !s.empty())
	{
		//先入左树,后入右树
		while (cur)
		{
			s.push(cur);
			cur = cur->left;
		}

		//检查右树
		cur = s.top();
		if (cur->right && cur->right != pre)  //右节点为空或者已访问则访问根节点
		{
			cur = cur->right;
		}
		else
		{
			cout << cur->val << " ";
			pre = cur;
			cur = NULL;
			s.pop();
		}
	}
}

广度优先遍历二叉树（层序遍历）

层序遍历是一种广度优先搜索（BFS）的方法，它按照树的层级顺序逐层访问节点。以下是层序遍历的关键步骤：

1，创建一个队列（通常使用队列来实现 BFS），并将根节点入队。

2，进入循环，直到队列为空。循环的条件是队列不为空，这保证了所有节点都能被访问到。

3，在循环中，首先从队列中取出队首节点，并访问该节点。这个节点是当前层级要访问的节点。

4，将当前节点的所有子节点（左子节点和右子节点）依次入队。这样可以保证下一轮循环时，访问的是下一层级的节点。

5，重复步骤 2 到步骤 4，直到队列为空，表示所有层级的节点都已经访问完毕。

代码实现：

void BinaryTreeLevelOrder(TreeNode* root)
{
	if (root == nullptr)
	{
		return;
	}
	queue<TreeNode*> q;
	q.push(root);
	while (!q.empty())
	{
		int len = q.size();
		for (int i = 0; i < len; i++)
		{
			TreeNode* p = q.front();
			q.pop();
			cout << p->val << " ";

			if (p->left)
				q.push(p->left);
			if (p->right)
				q.push(p->right);
		}
	}
}

翻转二叉树

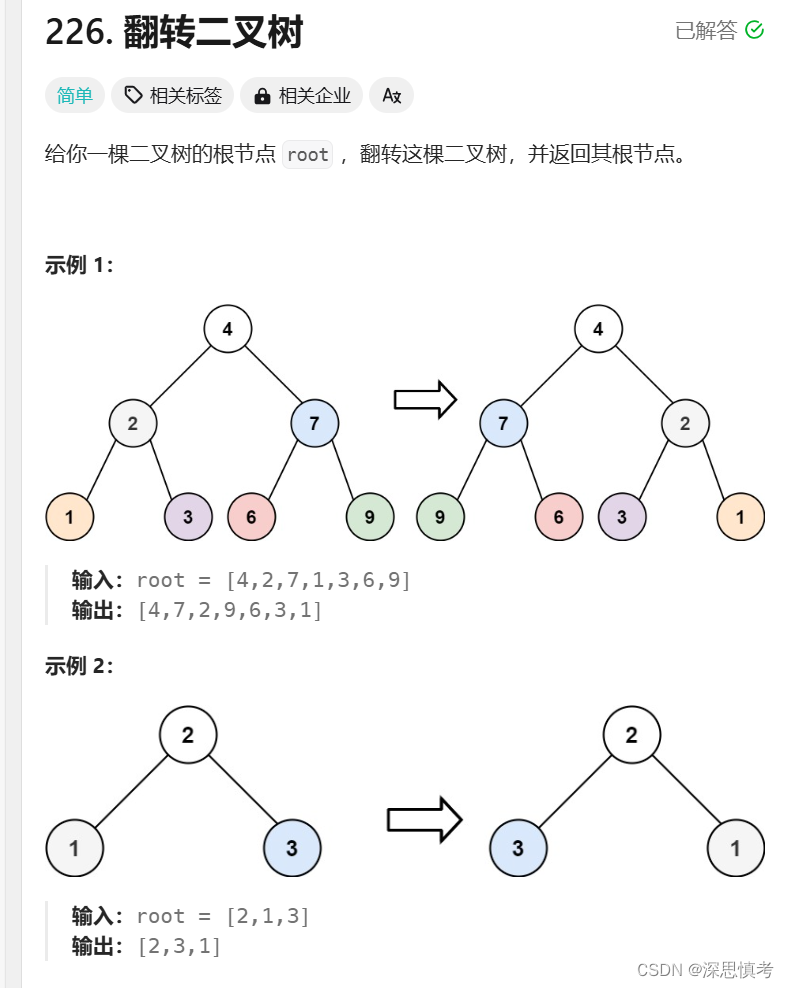
在这里插入图片描述

题目链接：翻转二叉树

递归方法：

1，递归终止条件：如果当前节点为空，直接返回。

2，递归反转：交换当前节点的左右子节点。

3，递归调用：分别对当前节点的左右子节点进行递归反转。

4，返回根节点：最后返回根节点，作为反转后的二叉树的根。

//递归翻转二叉树(左右树节点交换)
void Filp_Tree(TreeNode* root)
{
	if (root == NULL)
	{
		return;
	}

	swap(root->left, root->right);//函数
	Filp_Tree(root->left);
	Filp_Tree(root->right);
}

二叉树深度

最大深度

在这里插入图片描述
题目链接：二叉树的最大深度

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

理解如何计算二叉树的最大深度可以通过以下步骤来实现：

1，递归终止条件：如果当前节点为空，则返回深度 0。

2，递归计算：递归地计算左子树和右子树的最大深度。

3，深度计算：将左右子树的最大深度中较大的值加 1，表示当前节点的深度。

4，返回结果：返回左右子树中较大深度加上当前节点深度作为结果。

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点结构体
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

// 定义一个函数来计算二叉树的最大深度
int maxDepth(struct TreeNode* root) {
    // 如果根节点为空，说明树为空，最大深度为0
    if (root == NULL) {
        return 0;
    }
    
    // 递归计算左右子树的最大深度
    int left_depth = maxDepth(root->left);
    int right_depth = maxDepth(root->right);
    
    // 返回左右子树中较大深度加上根节点的深度（1）
    return left_depth > right_depth ? left_depth + 1 : right_depth + 1;
}

int main() {
    // 示例：构建一个二叉树
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->val = 2;
    root->left->left = NULL;
    root->left->right = NULL;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->val = 3;
    root->right->left = NULL;
    root->right->right = NULL;

    // 计算二叉树的最大深度
    int depth = maxDepth(root);
    printf("二叉树的最大深度为：%d\n", depth);

    // 释放二叉树内存
    free(root->left);
    free(root->right);
    free(root);

    return 0;
}

最小深度

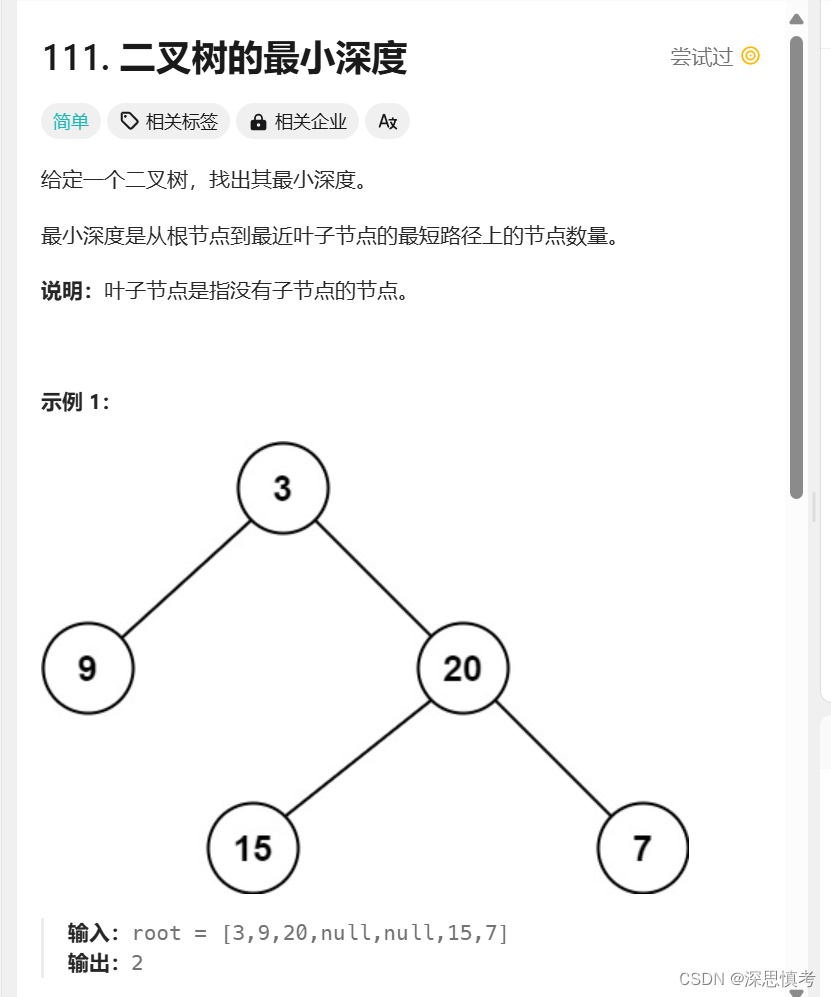
在这里插入图片描述

题目链接：最小深度

计算二叉树的最小深度是指从根节点到最近叶子节点的最短路径上的节点数。与计算最大深度类似，但有一些特殊情况需要处理。以下是计算二叉树最小深度的步骤：

1，递归终止条件：如果当前节点为空，则返回深度 0。

2，处理只有一个子树的情况：如果当前节点只有一个子树，那么需要递归计算另一侧子树的深度，并返回不为空的子树深度加 1。

3，递归计算：递归地计算左子树和右子树的最小深度。

4，深度计算：将左右子树的最小深度中较小的值加 1，表示当前节点的深度。

5，返回结果：返回左右子树中较小深度加上当前节点深度作为结果。

代码实现：

 int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        if (root->left == nullptr && root->right == nullptr) {
            return 1;
        }

        int min_depth = INT_MAX;
        if (root->left != nullptr) {
            min_depth = min(minDepth(root->left), min_depth);
        }
        if (root->right != nullptr) {
            min_depth = min(minDepth(root->right), min_depth);
        }

        return min_depth + 1;
    }

对称二叉树

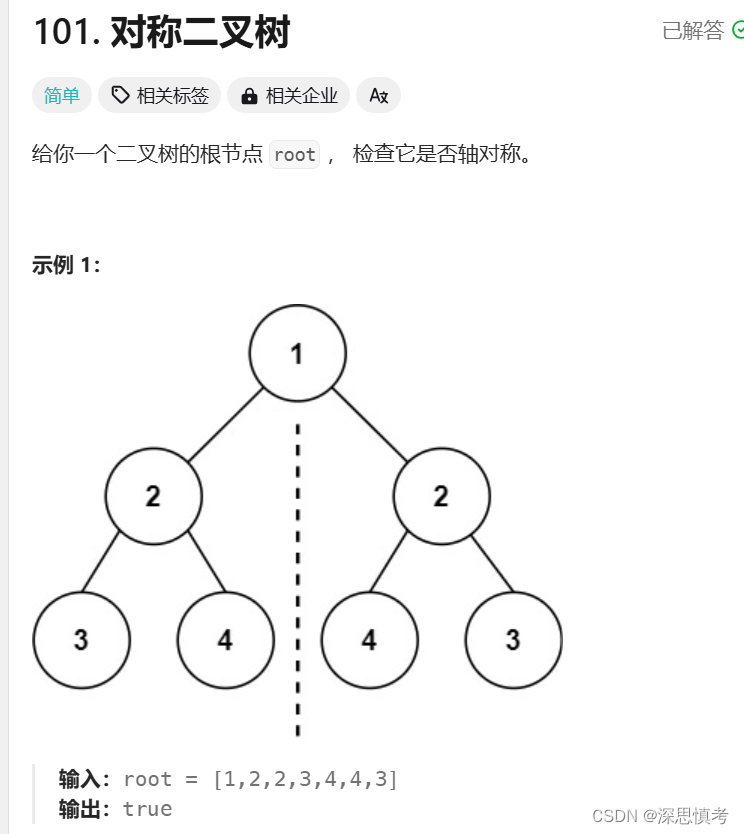
在这里插入图片描述
题目链接：对称二叉树

检查对称二叉树的思路主要是比较二叉树的左右子树是否镜像对称。以下是检查对称二叉树的步骤：

1，递归终止条件：如果当前节点为空，则返回 true。

2，递归比较：递归地比较左右子树的对称节点。

3，比较规则：对称节点的比较规则是左子树的左节点与右子树的右节点比较，左子树的右节点与右子树的左节点比较。

4，返回结果：如果所有对称节点都满足比较规则，则返回 true，否则返回 false。

#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点结构体
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

// 递归函数检查对称性
bool isMirror(struct TreeNode* left, struct TreeNode* right) {
    // 如果左右节点都为空，则对称
    if (left == NULL && right == NULL) {
        return true;
    }

    // 如果左右节点有一个为空，则不对称
    if (left == NULL || right == NULL) {
        return false;
    }

    // 如果左右节点的值不相等，则不对称
    if (left->val != right->val) {
        return false;
    }

    // 递归比较左子树的左节点与右子树的右节点，左子树的右节点与右子树的左节点
    return isMirror(left->left, right->right) && isMirror(left->right, right->left);
}

// 检查对称二叉树
bool isSymmetric(struct TreeNode* root) {
    // 调用递归函数检查对称性
    return isMirror(root, root);
}

int main() {
    // 示例：构建一个对称二叉树
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->val = 2;
    root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->left->val = 3;
    root->left->left->left = NULL;
    root->left->left->right = NULL;
    root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->right->val = 4;
    root->left->right->left = NULL;
    root->left->right->right = NULL;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->val = 2;
    root->right->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->left->val = 4;
    root->right->left->left = NULL;
    root->right->left->right = NULL;
    root->right->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->right->val = 3;
    root->right->right->left = NULL;
    root->right->right->right = NULL;

    // 检查对称二叉树
    if (isSymmetric(root)) {
        printf("二叉树是对称的\n");
    } else {
        printf("二叉树不是对称的\n");
    }

    // 释放二叉树内存
    free(root->left->left);
    free(root->left->right);
    free(root->left);
    free(root->right->left);
    free(root->right->right);
    free(root->right);
    free(root);

    return 0;
}