scikit-learn机器学习要点总结

- 一、机器学习总体流程
- 二、引入数据集
- 三、将数据集转换为DataFrame
- 四、可视化数据
- 五、数据预处理
- - （一）数据标准化
  - （二）独热编码
- 六、数据集划分为训练集和测试集
- 七、创建模型估计器(estimator)
- - （一）用于回归的估计器
  - （二）用于分类的估计器
- 八、用训练集训练模型估计器estimator
- 九、用模型估计器对测试集数据做预测
- 十、对模型估计器的学习效果进行评价
- 十一、网格搜索超参数
- 小结：几种分类算法的思想与优缺点
- - 1、KNN算法
  - 2、SVM算法
  - 3、Logistic回归

一、机器学习总体流程

在这里插入图片描述
总体处理流程可以分为：加载数据集、数据预处理、数据集划分、模型估计器创建、模型拟合、模型性能评估

机器学习的一般步骤通常包括以下几个阶段：

数据收集：收集与问题相关的数据，这可能涉及从不同来源获取数据，清洗数据以及对数据进行初步的探索性分析。
数据预处理：在这一阶段，需要对数据进行清洗、转换和归一化等操作，以便为模型训练做好准备。这可能包括处理缺失值、异常值和数据编码等。
特征工程：选择合适的特征对数据进行表征，并进行特征提取、转换和选择，以提高模型的性能。
模型选择与训练：选择合适的机器学习算法，并使用训练数据对模型进行训练。这可能涉及将数据划分为训练集、验证集和测试集，并对模型进行交叉验证等。
模型评估：使用测试集或交叉验证等方法对训练好的模型进行评估，以了解模型的泛化能力和性能。
模型优化：根据评估结果对模型进行调参和优化，以提高模型的性能。
模型部署与监测：将训练好的模型部署到实际应用场景中，并持续监测模型的性能，对模型进行更新和维护。

这些步骤并不是一成不变的，具体的应用场景和数据情况可能会导致步骤的顺序和内容有所不同。

二、引入数据集

sklearn机器学习库官方自带数据集：

在这里插入图片描述
以波士顿房价数据集和鸢尾花数据集为例：

#导入波士顿房价数据集
from sklearn.datasets import load_boston

#使用数据集时,以鸢尾花数据集为例
from sklearn.datasets import load_iris
iris=load_iris()
iris.keys()

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

三、将数据集转换为DataFrame

import pandas as pd
iris_data=pd.DataFrame(iris.data,columns=iris.feature_names)    #将数据集转换为DataFrame格式
iris_data['target']=iris.target_names[iris.target]    #将数据集的标签转换为DataFrame格式
iris_data.head(3).append(iris_data.tail(3))   #查看数据集的前三行和后三行

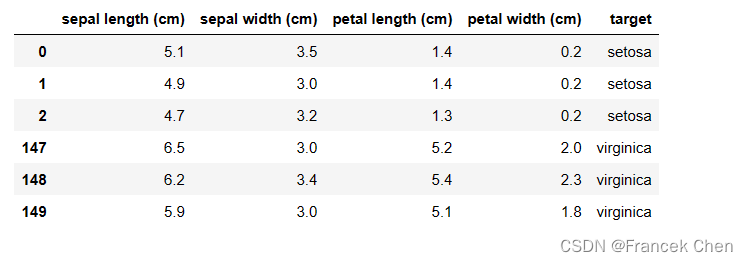
在这里插入图片描述

四、可视化数据

import seaborn as sns
sns.pairplot(iris_data,hue='target',palette='husl')   #根据目标类别着色绘制散点图矩阵

在这里插入图片描述

五、数据预处理

（一）数据标准化

from sklearn.preprocessing import StandardScaler
X=StandardScaler().fit_transform(iris.data)
y=iris.target
y

在这里插入图片描述

fit(), fit_transform(), 和 transform() 是在机器学习中常用的方法，用于数据预处理和模型训练过程中的特征处理。它们的功能略有不同：

fit()：这个方法用于对训练数据进行学习，即根据训练数据的特征分布或其他统计信息来估计模型参数。例如，在数据预处理过程中，fit() 方法可以计算并保存一些统计值（如均值、方差等）以供后续使用。
transform()：这个方法将学习到的模型参数应用于数据，对数据进行转换。例如，使用 fit() 计算得到的均值和方差可以在 transform() 中用来对数据进行标准化处理。
fit_transform()：这个方法是 fit() 和 transform() 的结合，既进行学习又进行转换。它首先使用训练数据进行学习，然后将学习到的模型参数应用于数据转换，返回转换后的结果。这个方法在某些情况下可以更高效，因为它同时执行了学习和转换步骤，避免了重复计算。

需要注意的是，fit_transform() 方法通常只能在训练数据上使用，而 transform() 方法可以在训练数据和测试数据上使用。这是因为在训练数据上学习得到的模型参数，需要一致地应用于训练数据和测试数据，以保持一致性和可比性。

总结起来，fit() 用于学习模型参数，transform() 用于将模型参数应用于数据转换，而 fit_transform() 则结合了二者，先学习再转换。具体使用哪个方法取决于任务的需求和数据处理的流程。

（二）独热编码

独热编码（One-Hot Encoding）是一种常用的分类变量处理方法，用于将具有有限个取值的离散特征转换为二进制向量表示。它的原理是为每个可能的取值创建一个新的二进制特征，并且在该特征中只有一个取值为1，其他取值都为0。

例如，假设有一个分类特征"颜色"，可能的取值有"红色"、“蓝色"和"绿色”。使用独热编码后，将创建三个新的二进制特征：“红色”，“蓝色"和"绿色”。对于每个样本，在相应的特征中，属于该类别的取值为1，其他特征都为0。

独热编码可以通过多种方式进行实现，其中最常见的是使用sklearn库中的OneHotEncoder类。在进行独热编码之前，需要先将字符串类型的数据转换为数值类型。在处理分类特征时，一种常见的方法是使用LabelEncoder类将字符串类型的数据转换为整数编码，然后再进行独热编码。下面是一个使用OneHotEncoder进行独热编码的示例：

from sklearn.preprocessing import LabelEncoder, OneHotEncoder

# 创建示例数据集
data = ['红色', '蓝色', '绿色', '红色', '绿色']

# 创建 LabelEncoder 对象并进行转换
label_encoder = LabelEncoder()
encoded_data = label_encoder.fit_transform(data)

# 对转换后的数据进行独热编码
encoder = OneHotEncoder()
encoded_data = encoder.fit_transform(encoded_data.reshape(-1, 1)).toarray()

# 打印编码后的结果
print(encoded_data)

在这里插入图片描述

运行上述代码，将得到一个独热编码后的数组，表示每个颜色的二进制特征表示。注意，fit_transform()方法同时执行了学习和转换步骤。

独热编码常用于机器学习中对分类特征的处理，它可以将分类变量转换为数值变量，使得机器学习算法能够更好地处理这些特征。但需要注意的是，应根据具体情况决定是否使用独热编码，因为它会增加特征维度，可能会导致维度灾难问题。

补充说明：划分训练集和测试集后，如果对训练集应用了fit_transform()方法，则测试集要使用同一预处理评估器的transform()方法。

fit_transform(X_train) ：找出X_train的均值和标准差，并应用在X_train上。对于X_test，直接使用transform方法。(此时StandardScaler已经保存了X_train的均值和标准差)

二者的功能都是对数据进行某种统一处理（比如标准化~N(0,1)，将数据缩放 (映射) 到某个固定区间，归一化，正则化等）
transform(restData)，从而保证train、rest处理方式相同。
如果fit_transfrom(trainData)后，使用fit_transform(restData)而不用transform(restData)，虽然也能归一化，但是两个结果不是在同一个“标准”下的，具有明显差异。

from sklearn import preprocessing
X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, test_size=0.4, random_state=0)
scaler = preprocessing.StandardScaler().fit(X_train)
X_train_transform = scaler.transform(X_train)
X_test_transform = scaler.transform(X_test)

六、数据集划分为训练集和测试集

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=33)

train_test_split()是一个常用于将数据集划分为训练集和测试集的函数，它通常用于机器学习模型的训练和评估过程。这个函数可以通过指定一些参数来完成数据集的划分。以下是一些常用的参数：

test_size：这是一个浮点数或整数，用于指定测试集的大小。如果是浮点数，表示测试集占总样本的比例；如果是整数，表示具体的测试集样本数量。
train_size：与 test_size 相反，如果指定了 train_size，则可以显式地设置训练集的大小。如果 test_size 未指定，则默认为 1 - train_size。
random_state：这是一个整数或者 random_state 实例，用于控制数据集的随机划分。设置相同的 random_state 将会使得每次划分的结果相同。
shufle：是否在分割前对数据集进行洗牌，默认值为True。如果设置为False，则按原始数据集的顺序进行划分。
stratify：如果指定了 stratify，则根据标签（类别）进行分层抽样，确保训练集和测试集中各类别样本的比例与原始数据集中相同。

补充说明：如果采用交叉验证，交叉验证应仅对训练集数据进行，而不能用于测试集的数据。

七、创建模型估计器(estimator)

（一）用于回归的估计器

1、线性回归

#线性回归
from sklearn.linear_model import LinearRegression
lr=LinearRegression()
#查看相关帮助：help(LinearRegression)

2、支持向量回归SVR

#支持向量回归SVR
from sklearn.svm import SVR
svr=SVR()
#查看相关帮助：help(SVR)

3、kNN用于回归

#kNN用于回归
from sklearn.neighbors import KNeighborsRegressor
knn_reg=KNeighborsRegressor()

（二）用于分类的估计器

1、逻辑回归用于分类

#逻辑回归用于分类
from sklearn.linear_model import LogisticRegression   #助记：把LinearRegression改成LogisticRegression即可
lgr=LogisticRegression()
#查看相关帮助：help(LogisticRegression)

2、支持向量用于分类

#支持向量用于分类：使用LinearSVC，只适用于线性可分的数据集，对于大数据集训练非常快，一般作为初始训练的首选
from sklearn.svm import LinearSVC
lsvc=LinearSVC()

#支持向量用于分类：使用SVC，适用于线性可分和不可分的数据集(通过使用核函数)，性能不如LinearSVC
from sklearn.svm import SVC
svc=SVC()

3、kNN用于分类

#kNN用于分类
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()

八、用训练集训练模型估计器estimator

#根据需要，用具体的上文估计器去替换下面的estimator
#estimator.fit(X_train,y_train)
knn.fit(X_train,y_train)

KNeighborsClassifier()

九、用模型估计器对测试集数据做预测

#根据需要，用具体的上文估计器去替换下面的estimator
#y_pred=estimator.predict(X_test)
y_pred=knn.predict(X_test)

十、对模型估计器的学习效果进行评价

最简单的评估方法：就是调用估计器的score()，该方法的两个参数要求是测试集的特征矩阵和标签向量。

对于回归问题，score()返回的结果就是r2_score
对于分类问题，score()返回的结果就是下面的ACC

#根据需要，用具体的上文估计器去替换下面的estimator
#print(estimator.score(X_test,y_test))
print(knn.score(X_test,y_test))

#对于二分类问题，还可以使用metrics子包中的confusion_matrix()、precision_score()、recall_score、accuracy_score()等
#这些方法的参数分别是测试集的真实标签和预测标签
from sklearn import metrics
confusion_matrix = metrics.confusion_matrix(y_test,y_pred)       # 混淆矩阵（注意与上面示例的混淆矩阵的图位置并不一一对应）
#recall_score = metrics.recall_score(y_test,y_pred)               # 召回率(查全率)=tp/(tp+fn)
#pre_score = metrics.precision_score(y_test,y_pred)               # 准确率(查准率)=tp/(tp+fp)
ACC = metrics.accuracy_score(y_test,y_pred)                      # 准确度ACC=(tp+tn)/(tp+tn+fp+fn)
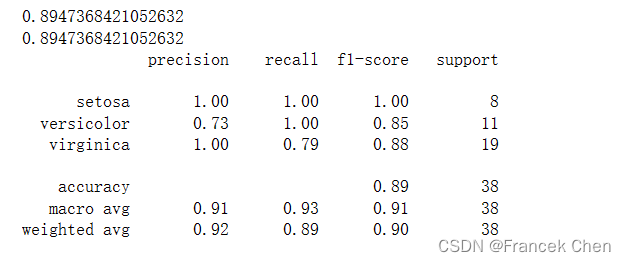
print(ACC)

#对于多分类问题，还可以使用metrics子包中的classification_report
print(metrics.classification_report(y_test,y_pred,target_names=iris.target_names))

在这里插入图片描述

十一、网格搜索超参数

超参数说明：模型参数 (如果有的话，例如SVM中分离超平面的法向量w和截距b) 是通过fit()方法从数据中学习到的，而超参数则是人工配置的，因而创建模型对象时指定的参数是超参数。

为了评估不同超参数组合配置下的模型性能，可以采用网格搜索的方法,并且常常与训练数据集的交叉验证进行搭配。

网格搜索的目的是为了优化超参数配置，交叉验证的目的是为了更准确的评估特定超参数配置下的模型性能的可信度，两者作用不同。

网格搜索与交叉验证相结合的kNN算法分类：

#使用stratify参数进行分层采样
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=33,stratify=iris.target) 

from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier()

from sklearn.model_selection import GridSearchCV,KFold
params_knn={'n_neighbors':range(3,10,1)}
kf=KFold(n_splits=5,shuffle=False)

grid_search_knn=GridSearchCV(neigh,params_knn,cv=kf)
grid_search_knn.fit(X_train,y_train)
grid_search_y_pred=grid_search_knn.predict(X_test)
print("Accuracy:",grid_search_knn.score(X_test,y_test))
print("best params:",grid_search_knn.best_params_)

在这里插入图片描述

可见引入网格搜索时，只要把原来的估计器、搜索参数和交叉验证对象 (或交叉验证折数) 作为参数去创建一个网格搜索估计器，后面凡是原估计器出现的地方都用网格搜索估计器替代即可。

交叉验证：

KFold()函数是用于将数据集进行K折交叉验证的函数，它可以帮助我们评估模型的性能并减小因数据集划分不同而引起的偏差。在使用KFold()函数时，可以指定将数据集划分为多少个折（即K的取值），然后对每一折进行训练和验证。

以下是KFold()函数的一些常用参数：

n_splits：指定将数据集划分为多少个折（即K的取值）。
shuffle：布尔值，表示是否在划分之前对数据进行洗牌，以确保数据的随机性。
random_state：整数或者 random_state 实例，用于控制数据的洗牌过程。
stratified：是否进行分层抽样，默认值为False。如果设置为True，则会进行分层抽样，即保证每个子集中的样本类别比例与原始数据集中的样本类别比例相同。stratified通常用于处理分类问题。

KFold()函数通常配合交叉验证函数（如 cross_val_score()）一起使用，以评估模型的性能。以下是一个示例，展示了如何使用KFold()函数：

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression

# 创建 KFold 对象
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# 创建模型
model = LogisticRegression()

# 使用交叉验证评估模型性能
scores = cross_val_score(model, X, y, cv=kf)
print("交叉验证结果：", scores)
print("平均准确率：", scores.mean())

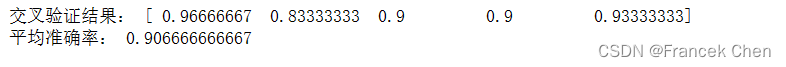
在这里插入图片描述

在这个示例中，我们首先创建了一个KFold对象，并指定了将数据集划分为5折交叉验证，并设置了洗牌和随机种子参数。然后我们创建了一个逻辑回归模型，在使用cross_val_score()函数进行交叉验证评估模型性能。cross_val_score()函数会自动使用KFold对象进行交叉验证，并返回每一折验证的性能评分。

Gridsearchcv()函数是用于网格搜索和交叉验证的函数，它通过遍历给定的参数组合来寻找最佳的模型超参数。该函数可以帮助我们系统地搜索不同的超参数组合，并使用交叉验证来评估每个超参数组合的性能，从而找到最优的模型配置。以下是GridSearchCV()函数的一些常用参数：

estimator：指定要优化的机器学习模型或者管道对象。
param_grid：一个字典或列表，包含要搜索的超参数及其取值范围。可以使用字典表示多个参数的组合，也可以使用列表表示单个参数的不同取值。
scoring：指定模型性能评估的指标，可以是字符串（如 ‘accuracy’）或者可调用函数。
cv：用于交叉验证的折数，默认为 5，可以是一个整数或者交叉验证生成器对象。
refit：布尔值，表示是否在搜索结束后重新训练最佳模型，并将其保存在 estimator 中。

以下是一个示例，展示了如何使用GridSearchCV()函数进行超参数调优：

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 创建 GridSearchCV 对象
param_grid = {'C': [0.1, 1, 10], 'gamma': [0.001, 0.01, 0.1]}
grid_search = GridSearchCV(estimator=SVC(), param_grid=param_grid, scoring='accuracy', cv=5)

# 在训练集上拟合 GridSearchCV 对象
grid_search.fit(X_train, y_train)

# 打印最佳超参数和对应的模型性能
print("最佳超参数：", grid_search.best_params_)
print("最佳模型性能：", grid_search.best_score_)

在这里插入图片描述

在这个示例中，我们首先创建了一个GridSearchCV对象，并指定了要优化的模型（这里使用了支持向量机模型 SVC），以及要搜索的超参数组合param_grid。然后我们使用训练集数据对GridSearchCV对象进行拟合。拟合完成后，我们可以通过best_params_属性获取最佳超参数组合，通过best_score_属性获取对应的模型性能。