正则表达式
正则表达式是一种用来描述正则语言的更紧凑的表达方法
e.g.
r
=
a
(
a
∣
b
)
∗
(
ϵ
∣
(
.
∣
)
(
a
∣
b
)
)
r=a(a|b)^*(\epsilon|(.|\\_ )(a|b))
r=a(a∣b)∗(ϵ∣(.∣)(a∣b))
正则表达式可以由较小的正则表达式按照特定的规则递归地构建。每个正则表达式定义的语言记作 L(r)。
正则表达式的定义
空字符是一个正则表达式,则
L
(
ϵ
)
=
ϵ
L(\epsilon) = \\{\epsilon\\}
L(ϵ)=ϵ
属于字母表中的字母 a为一个正则表达式,则
L
(
a
)
=
a
L(a) = \\{a\\}
L(a)=a
假设 r 和 s 都是正则表达式,表示的语言分别是 L(r)和 L(s)
则:
(1)r|s 是一个正则表达式:L(r|s)=L(r)并 L(s)
(2)rs 是一个正则表达式,L(rs) = L(r)L(s)
(3)r是正则表达式,其语言等于 r 语言的闭包
(4)(r)的语言就是 r 的语言
这四个运算的优先级从高到低分别是:,连接,|
e.g.
∑
=
a
,
b
\sum = \\{a,b\\}
∑=a,b
L(a|b) ={a,b}
L((a|b)(a|b))={aa,ab,ba,bb}
L(a*) = (L(a))** = {a}* = {epsilon,a,aa,…}
十进制整数:(1|…|9)(0|…|9)|0
八进制整数:0(1|…|7)(0|…|7)
正则语言
可以用正则表达式定义的语言叫做正则语言
正则表达式的代数定律
(1)|具有交换律结合律
(2)连接具有结合律
(3)连接对|具有分配律
(4)epsilon 可以作为连接的单位元:
ϵ
s
=
s
ϵ
=
s
\epsilon s = s \epsilon = s
ϵs=sϵ=s
(5)闭包中一定包含 epsilon
(6)克林闭包具有幂等性
正则定义
正则定义是具有如下形式的定义red:序列:
d
i
→
r
i
d_i \to r_i
di→ri
其中 di 均不相同,且都不在字母表中
每一个 ri 均为字母表中的符号,或者为已经定义过的正则表达式
e.g.
d
i
g
i
t
→
0
∣
1
∣
.
.
.
∣
9
digit \to0|1|...|9
digit→0∣1∣...∣9
KaTeX parse error: Expected group after '_' at position 30: …..|Z|a|...|z|\\_̲
i
d
e
n
t
i
f
i
e
r
→
l
e
t
t
e
r
(
l
e
t
t
e
r
∣
d
i
g
i
t
)
∗
identifier \to letter(letter|digit)^*
identifier→letter(letter∣digit)∗
这三条式子合在一起就完成了对 identifier 的定义
自动机
有穷自动机
Finite Automata,是对一类处理系统建立的数学模型
这类系统具有一系列离散的输入输出信息和有穷的内部状态
系统只需要根据当前的状态和当前面临的输入信息就可以决定系统的后继行为,每当系统处理了当前的输入,内部状态就会发生改变
e.g.电梯控制装置
不需要知道先前全部的状态,只需要知道当前状态与还未满足的状态
e.g. 图灵机
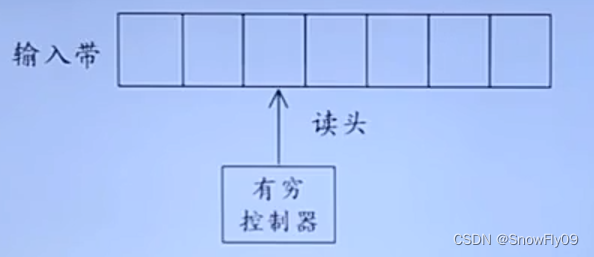
输入带用来存放符号串
读头用来从左至右逐个读取输入符号,不能够修改或者往返移动
有穷控制器:具有有穷个状态数,根据当前状态和当前输入符号转入下一个状态
转换图
结点:有穷自动机的状态
初始状态:只能有一个,用start 表示
终止状态:可以有多个,用双圈表示
带标记的有向边:如果对于输入 a,存在一个从状态 p 到 q 的转换,就在 p,q 之间
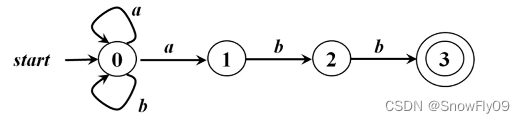
FA 接收的语言
给定输入串 x,如果存在一个对应于 x 的从初始状态到终止状态的序列,就可以被接受
由一个有穷自动机 M 接受的所有串构成的集合称为是该 FA 接收的语言,记为 L(M)
上图中自动机接受的语言即为所有以 abb 结尾的{a,b}上的串的集合
最长子串匹配原则
当输入串的多个前缀与一个或多个模式匹配时,总是选择最长的前缀进行匹配
因此尽管到达某个终态,只要还存在有向边带符号指向其他节点,FA 就继续前进,寻找尽可能长的匹配
e.g. x=-1
s
t
a
r
t
→
0
→
<
1
→
=
2
start\to 0 \to^<1\to^=2
start→0→<1→=2
-1<1,-1<=2
故根据最长子串匹配原则,应该到 2 为结束状态
有穷自动机的分类
确定的有穷自动机 DFA
M
=
(
S
,
∑
,
δ
,
s
0
,
F
)
M = (S,\sum,\delta,s_0,F)
M=(S,∑,δ,s0,F)
S 表示有穷状态集
SUM 表示输入字母表,这里假设空字符不属于输入字母表
delta 为 S * SUM 到 S 的映射,表示从状态 s 出发,沿着有向边 a 能够到达的状态
s0 开始状态
F 终止状态的red:集合
非确定有穷自动机NFA
与有穷状态机的区别
沿着有向边 a 可能到达多个状态,故 delta 表示 S*SUM 映射到 2^S 的集合
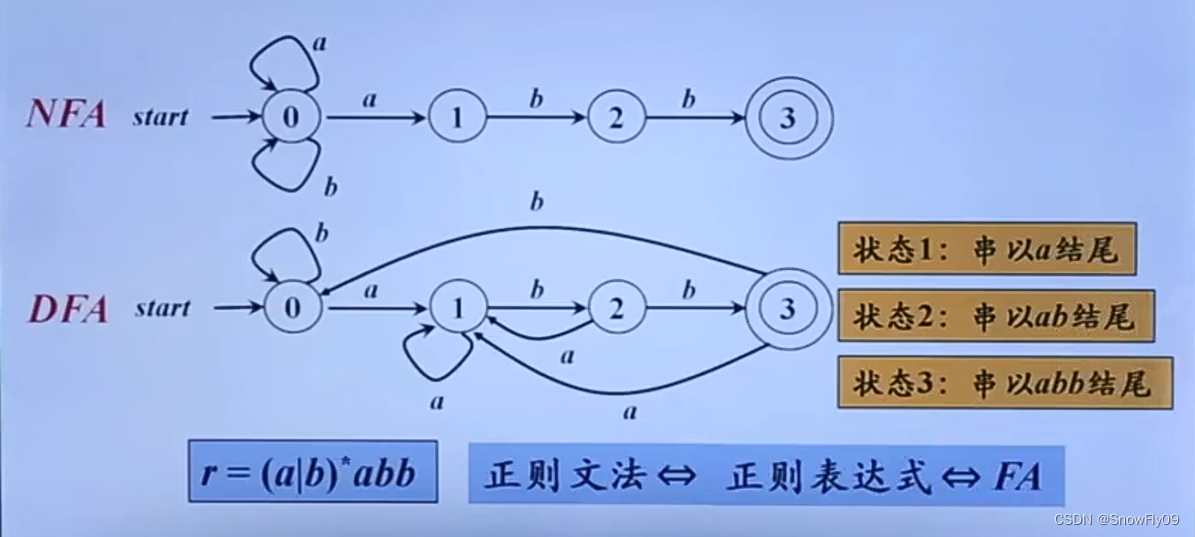
DFA 和 NFA 具有等价性
对于任何 NFA,有 DFA 可以识别同一语言
对于任何 DFA,有 NFA 可以识别同一语言
带有空边的 NFA
带空边的有向线段从一个状态指向另一个状态代表了不需要条件就可离开当前状态,类似串联一系列 if,当满足某个 if的时候就会停留在该状态并处理对应的程序,随后继续向下检验其他 if
带有空边的 NFA 和不带空边的 NFA 也可以等价:
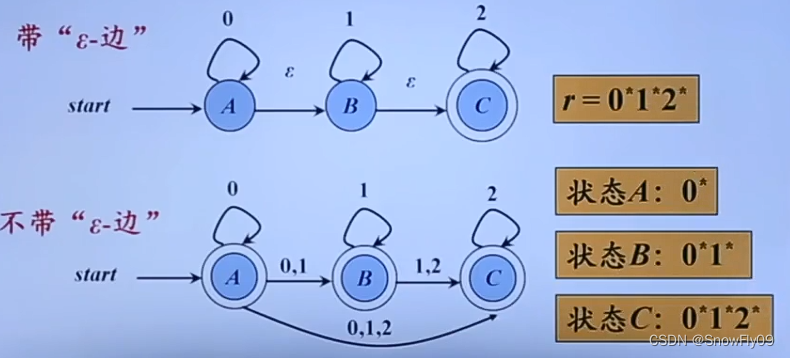
DFA 的算法实现
s
=
s
0
s = s_0
s=s0
c
=
n
e
x
t
C
h
a
r
(
)
;
c = nextChar();
c=nextChar();
KaTeX parse error: Expected '}', got 'EOF' at end of input: …ile (e!=eof)\\{
$ s=move(s,c);$
c
=
n
e
x
t
C
h
a
r
(
)
;
c = nextChar();
c=nextChar();
i
f
s
∈
F
r
e
t
u
r
n
y
e
s
if s \in F \\ return \\ yes
ifs∈Freturnyes
e
l
s
e
f
a
l
s
e
else \\ false
elsefalse
从正则表达式到DFA
往往需要 NFA 作为中介
对于空字 epsilon/字母表中符号 a
s
t
a
r
t
→
q
0
→
ϵ
q
f
start \to q_0 \to^\epsilon q_f
start→q0→ϵqf
s
t
a
r
t
→
q
0
→
a
q
f
start \to q_0 \to^a q_f
start→q0→aqf
其余运算对应的 NFA:
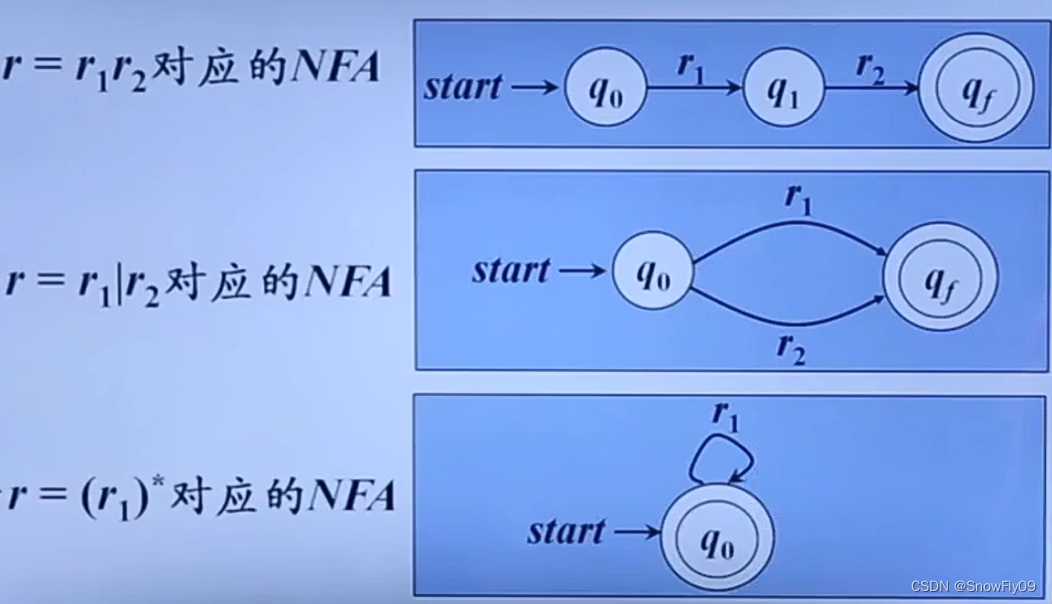
从 NFA 到 DFA
子集构造法:首先将 NFA 图改写成转换表
然后具体去写
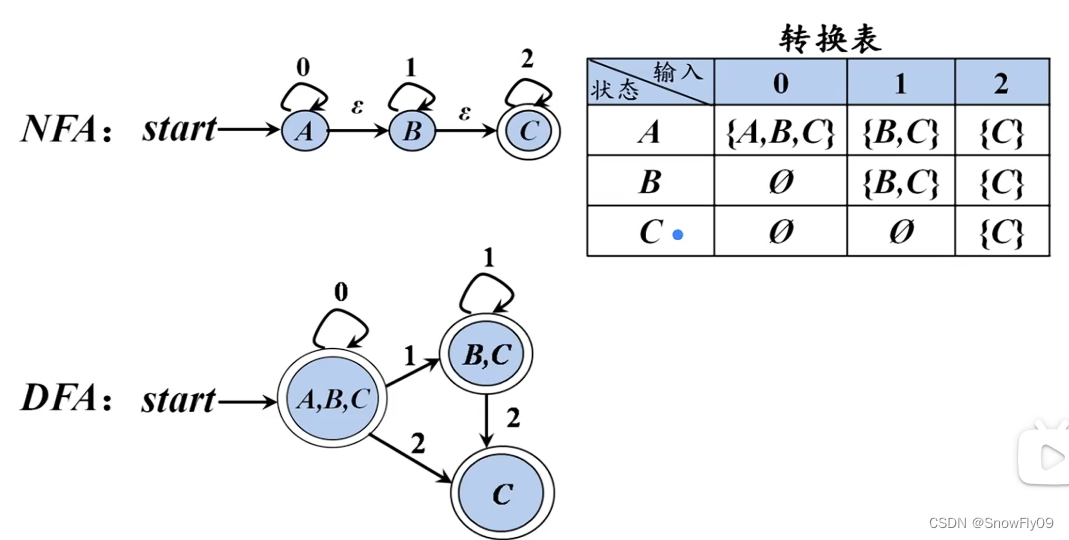
识别标识符的 DFA
d
i
g
i
t
→
0
∣
1
∣
.
.
.
∣
9
digit \to0|1|...|9
digit→0∣1∣...∣9
KaTeX parse error: Expected group after '_' at position 30: …..|Z|a|...|z|\\_̲
i
d
e
n
t
i
f
i
e
r
→
l
e
t
t
e
r
(
l
e
t
t
e
r
∣
d
i
g
i
t
)
∗
identifier \to letter(letter|digit)^*
identifier→letter(letter∣digit)∗
根据识别标识符的正则定义,我们可以首先获得其 NFA
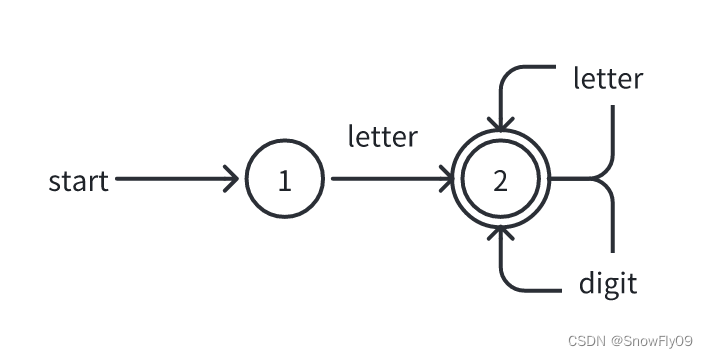
此时的 NFA 与 DFA 相等,所以不用再进行转换
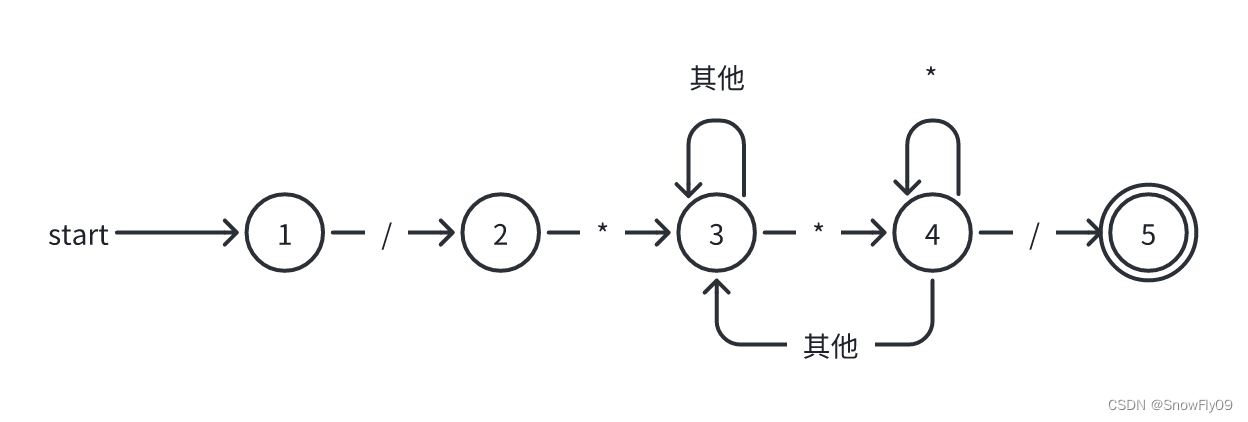
识别注释的 DFA
在确定一个状态机的时候首先要确保正则定义是正确的,否则无法写出正确的状态机