题解:寻找峰值(二分算法)
目录
- 1.题目
- 2.暴力求解
- 3.二分算法
- 4.总结
1.题目
题目链接:LINK

2.暴力求解
暴力求解的思路很简单,这个数组的形状无非就三种:
- 一直上升
- 下降(这里包含先下降后上升)
- 先升后降
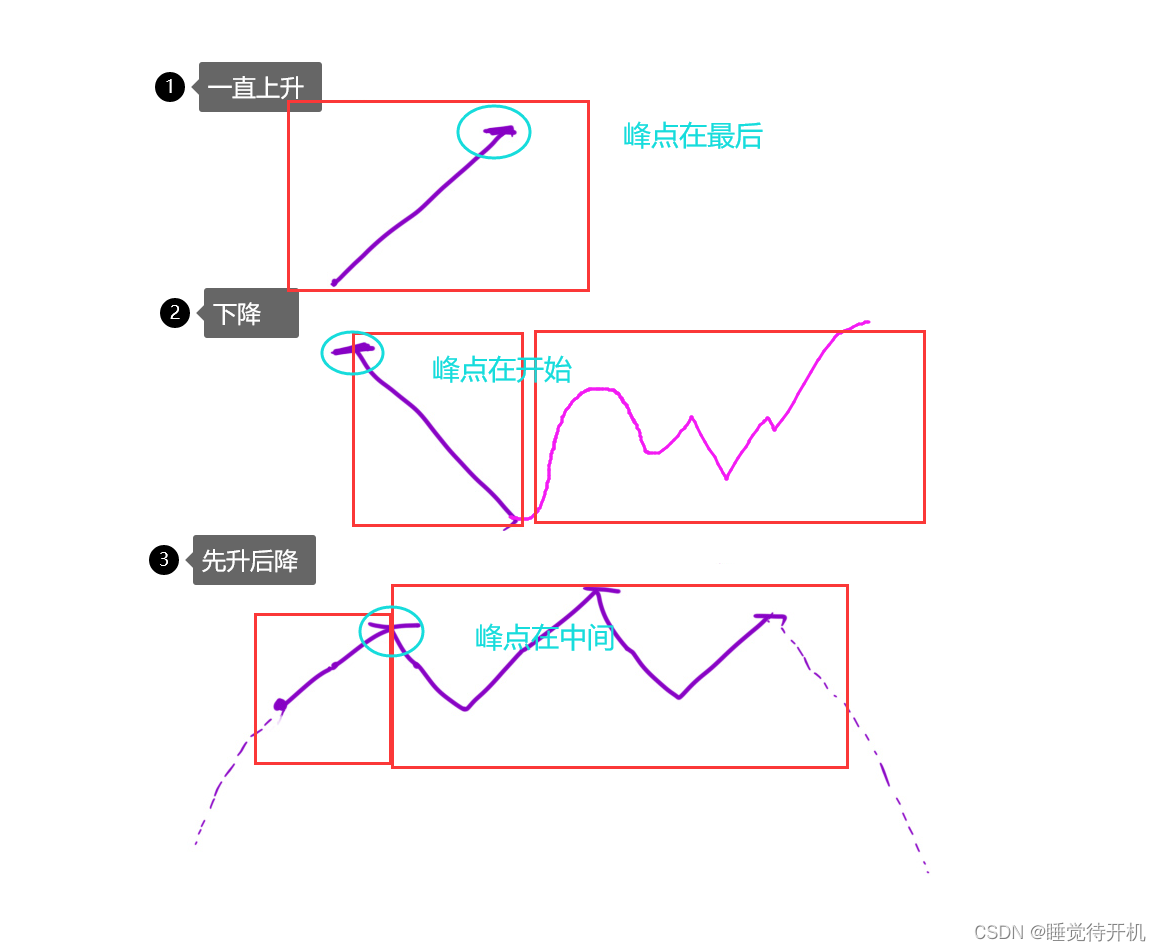
总结一下规律:
只要有下降,那么一定就是其中一个峰点了,实在一个数组里没有任何下降的,那就是最后一个数字的下标
然后代码就可以出炉了:时间复杂度:O(N)
class Solution {
public:
//暴力求解
int findPeakElement(vector<int>& nums)
{
for(size_t i = 0; i < nums.size() - 1; i++)
{
//出现下降
if(nums[i] > nums[i+1]) return i;
}
return nums.size() - 1;
}
};
细节:i的取值:
小细节就是i的取值是小于size() - 1,也就是说最多取到倒数第二个数,原因就是里面用到了mid + 1,如果mid可以取到最后一个数,那么mid + 1就是越界访问了。
3.二分算法
这个题目显然是提示咱们用二分算法了:
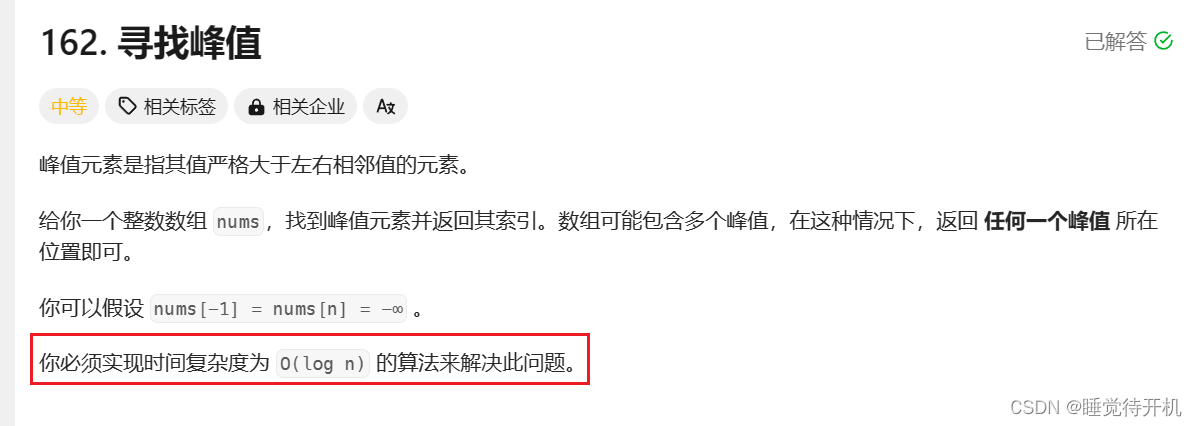
至于为什么可以用二分算法呢?
答案是具有二段性:
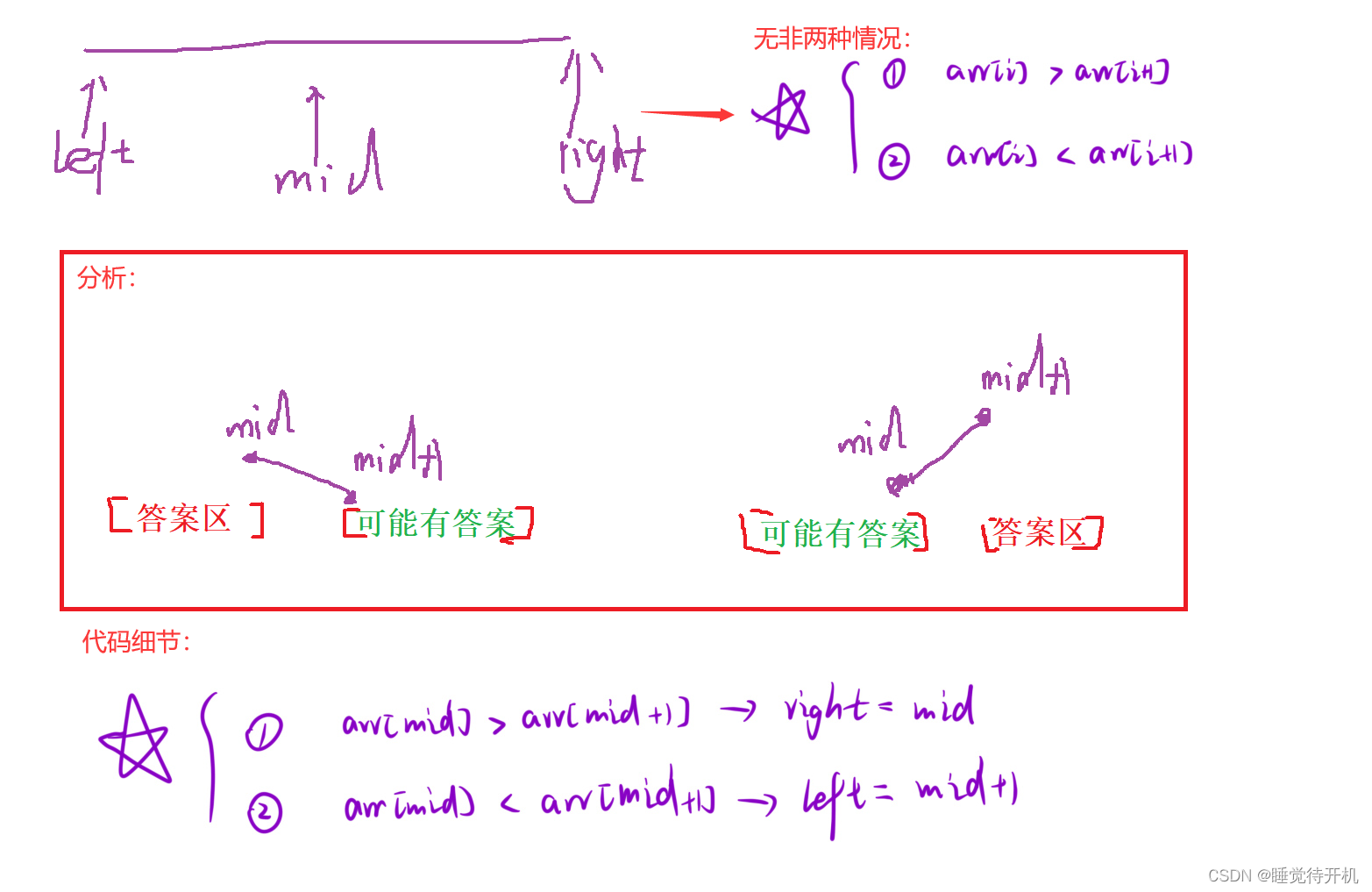
所以,我们可以得出二分代码:
class Solution {
public:
//二分算法
int findPeakElement(vector<int>& nums)
{
int left = 0, right = nums.size() - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > nums[mid + 1]) right = mid;
else left = mid + 1;
}
return left;
}
};
4.总结
感觉这个题的二分重点是mid与其后面的一个数进行比较得结果,需要自己把握这一点才行。
EOF