直接法的引出
因为第7讲大部分都是讲特征点法,通过提取orb特征点和点的描述子,来构建两帧图像之间的特征点对应关系。这种方法会有缺点:
- 关键点和描述子提取计算耗时,如果相机的频率高,则slam算法大部分耗时被占。
- 特征点是稀疏的,往往只有几百个,而且在我看来容易被一些动态物体干扰,就会对后续匹配造成影响。
- 在一些特征不明显的地方,大白墙或者没有明显角点的地方,特征点难提取,对后续计算相机运动造成影响。
光流法
光流可以分成稀疏光流和稠密光流。Lucas-Kanade光流跟踪部分像素点的运动成为稀疏光流,Horn-Schunck光流跟踪所有像素点的运动成为稠密光流。而书中主要是介绍了LK稀疏光流法。
个人见解
光流法的作用就是用来跟踪上一帧图片的像素点在当前帧图片中的位置,本质上也是特征匹配的一种方法,只是特征点法的特征匹配是通过点的描述子来进行匹配,而LK光流从图像入手,在灰度不变假设上,根据两帧图像求出跟踪像素点的运动速度,从而在第二帧图片中找到跟踪点的像素。后续就是简单列一下书里的公式。
公式推导
将图片看成是关于时间(t)和像素(u,v)的函数,即三元函数。根据灰度不变假设,对于t时刻在第一帧图片(x,y)的像素,根据灰度不变:
I
(
x
+
d
x
,
y
+
d
y
,
t
+
d
t
)
=
I
(
x
,
y
,
t
)
\boldsymbol{I}(x+\mathrm{d} x, y+\mathrm{d} y, t+\mathrm{d} t)=\boldsymbol{I}(x, y, t)
I(x+dx,y+dy,t+dt)=I(x,y,t)
然后就是经典的一阶泰勒展开:
I
(
x
+
d
x
,
y
+
d
y
,
t
+
d
t
)
≈
I
(
x
,
y
,
t
)
+
∂
I
∂
x
d
x
+
∂
I
∂
y
d
y
+
∂
I
∂
t
d
t
\boldsymbol{I}(x+\mathrm{d} x, y+\mathrm{d} y, t+\mathrm{d} t) \approx \boldsymbol{I}(x, y, t)+\frac{\partial \boldsymbol{I}}{\partial x} \mathrm{~d} x+\frac{\partial \boldsymbol{I}}{\partial y} \mathrm{~d} y+\frac{\partial \boldsymbol{I}}{\partial t} \mathrm{~d} t
I(x+dx,y+dy,t+dt)≈I(x,y,t)+∂x∂I dx+∂y∂I dy+∂t∂I dt
因为灰度不变,所以只剩三项:
∂
I
∂
x
d
x
+
∂
I
∂
y
d
y
+
∂
I
∂
t
d
t
=
0
\frac{\partial \boldsymbol{I}}{\partial x} \mathrm{~d} x+\frac{\partial \boldsymbol{I}}{\partial y} \mathrm{~d} y+\frac{\partial \boldsymbol{I}}{\partial t} \mathrm{~d} t=0
∂x∂I dx+∂y∂I dy+∂t∂I dt=0
然后就是除dt移项
∂
I
∂
x
d
x
d
t
+
∂
I
∂
y
d
y
d
t
=
−
∂
I
∂
t
\frac{\partial \boldsymbol{I}}{\partial x} \frac{\mathrm{d} x}{\mathrm{~d} t}+\frac{\partial \boldsymbol{I}}{\partial y} \frac{\mathrm{d} y}{\mathrm{~d} t}=-\frac{\partial \boldsymbol{I}}{\partial t}
∂x∂I dtdx+∂y∂I dtdy=−∂t∂I
对于上面这个式子,
d
x
/
d
t
dx/dt
dx/dt和
d
y
/
d
t
dy/dt
dy/dt就是我们要求的像素点的运动速度,记为u和v。其他项就是图像关于x,y,t的梯度,通过opencv或者自己去计算都可以求。最终就有
[
I
x
I
y
]
[
u
v
]
=
−
I
t
\left[\begin{array}{ll}\boldsymbol{I}_x & \boldsymbol{I}_y\end{array}\right]\left[\begin{array}{l}u \\ v\end{array}\right]=-\boldsymbol{I}_t
[IxIy][uv]=−It
但是只有一个像素点只有一个方程,所以一般是假设在点附近的一个窗口具有同样的运动,所以取一个w*w的窗口,就有
w
2
w^2
w2个方程
[
I
x
I
y
]
k
[
u
v
]
=
−
I
t
k
,
k
=
1
,
…
,
w
2
\left[\begin{array}{ll}\boldsymbol{I}_x & \boldsymbol{I}_y\end{array}\right]_k\left[\begin{array}{l}u \\ v\end{array}\right]=-\boldsymbol{I}_{t k}, \quad k=1, \ldots, w^2
[IxIy]k[uv]=−Itk,k=1,…,w2
这个就是用经典最小二乘法即可求出u和v,因为两帧图像的时间差是已知的,所以就可以在当前帧得到上一帧的对应点位置。
代码实现
书中除了直接用opencv去实现光流,同样通过高斯牛顿手写了一个光流法。本质上是求解一个优化问题:
min
Δ
x
,
Δ
y
∥
I
1
(
x
,
y
)
−
I
2
(
x
+
Δ
x
,
y
+
Δ
y
)
∥
2
2
\min _{\Delta x, \Delta y}\left\|\boldsymbol{I}_1(x, y)-\boldsymbol{I}_2(x+\Delta x, y+\Delta y)\right\|_2^2
Δx,Δymin∥I1(x,y)−I2(x+Δx,y+Δy)∥22
这个写法有点像直接法的光度误差,只不过目标不一样,光流法求的是上一帧跟踪像素点在当前帧图片的像素位置。那么对应的雅可比就是
I
2
I_2
I2在
x
+
Δ
x
,
y
+
Δ
y
x+\Delta x, y+\Delta y
x+Δx,y+Δy 处的梯度。但是这样子的定义感觉是有些歧义,最好是把
x
+
Δ
x
,
y
+
Δ
y
x+\Delta x, y+\Delta y
x+Δx,y+Δy当成一个整体
x
2
,
y
2
x_2,y_2
x2,y2,优化目标就是
x
2
,
y
2
x_2,y_2
x2,y2(即跟踪点在第二帧图片的位置)。

这样展开才能说得过去对应的雅可比就是
I
2
I_2
I2在
x
+
Δ
x
,
y
+
Δ
y
x+\Delta x, y+\Delta y
x+Δx,y+Δy 处的梯度。也可以参考SLAM光流法、直接法代码踩坑记录
然后后续程序就是基于单层光流去构建构建图像金字塔从粗到细实现多层光流,多层光流实际上可以帮助整个优化问题更好逼近全局最优解,而不是受图像梯度影响陷入局部最优。
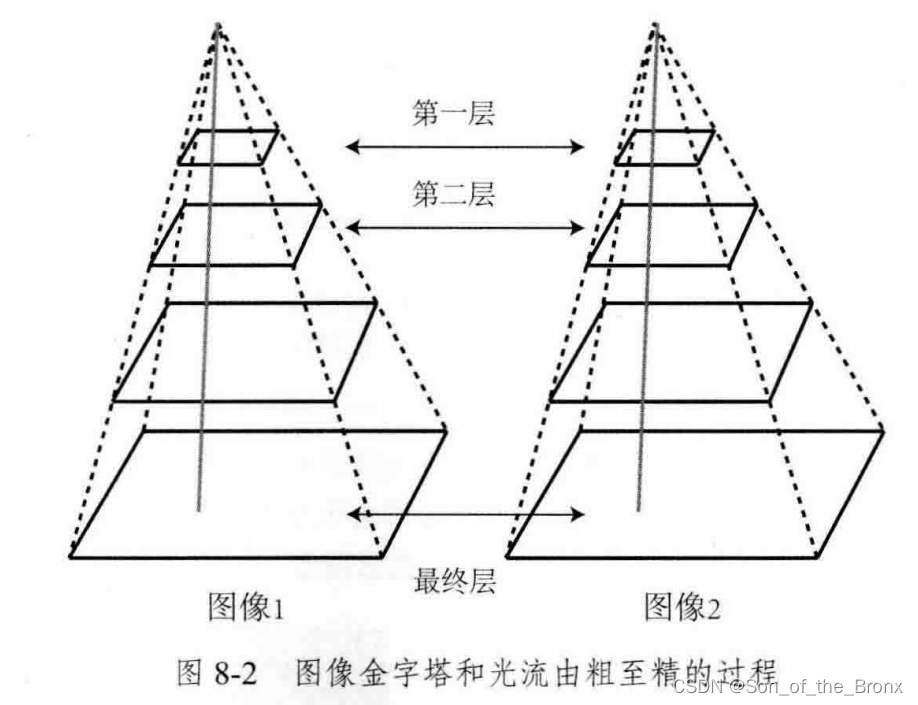
代码结果
很明显在目标函数优化后的误差,多层光流是优于单层光流的,也证明了多层光流的有效性。
直接法
直接法根据像素点的数量,可以分成稀疏、稠密和半稠密三种。与上面LK光流的区别在于,直接法通过构建两帧图片之间的光度误差,来直接优化两帧的R和t。而LK光流只是完成了像素点跟踪的问题。
公式推导
用下书的原图:
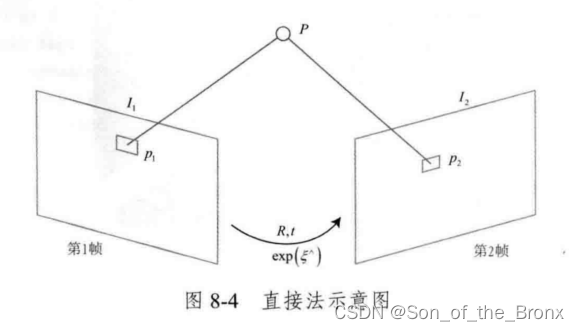
对于同一个三维点P,有下面的式子:其实就是相机模型的式子
p
1
=
[
u
v
1
]
1
=
1
Z
1
K
P
,
p
2
=
[
u
v
1
]
2
=
1
Z
2
K
(
R
P
+
t
)
=
1
Z
2
K
(
T
P
)
1
:
3
.
\begin{aligned} & \boldsymbol{p}_1=\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]_1=\frac{1}{Z_1} \boldsymbol{K} \boldsymbol{P}, \\ & \boldsymbol{p}_2=\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]_2=\frac{1}{Z_2} \boldsymbol{K}(\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t})=\frac{1}{Z_2} \boldsymbol{K}(\boldsymbol{T} \boldsymbol{P})_{1: 3} .\end{aligned}
p1=
uv1
1=Z11KP,p2=
uv1
2=Z21K(RP+t)=Z21K(TP)1:3.
然后就是通过光度误差构建优化问题。
e
=
I
1
(
p
1
)
−
I
2
(
p
2
)
e=\boldsymbol{I}_1\left(\boldsymbol{p}_1\right)-\boldsymbol{I}_2\left(\boldsymbol{p}_2\right)
e=I1(p1)−I2(p2)
min
T
J
(
T
)
=
∥
e
∥
2
\min _{\boldsymbol{T}} J(\boldsymbol{T})=\|e\|^2
minTJ(T)=∥e∥2
对于多个空间点就能构成多个误差项
min
T
J
(
T
)
=
∑
i
=
1
N
e
i
T
e
i
,
e
i
=
I
1
(
p
1
,
i
)
−
I
2
(
p
2
,
i
)
\min _{\boldsymbol{T}} J(\boldsymbol{T})=\sum_{i=1}^N e_i^{\mathrm{T}} e_i, \quad e_i=\boldsymbol{I}_1\left(\boldsymbol{p}_{1, i}\right)-\boldsymbol{I}_2\left(\boldsymbol{p}_{2, i}\right)
TminJ(T)=i=1∑NeiTei,ei=I1(p1,i)−I2(p2,i)
接下来就是去求误差对位姿T的雅可比。定义两个中间变量:
q
=
T
P
,
u
=
1
Z
2
K
q
\begin{aligned} \boldsymbol{q} & =\boldsymbol{T} \boldsymbol{P}, \\ \boldsymbol{u} & =\frac{1}{Z_2} \boldsymbol{K} \boldsymbol{q} \end{aligned}
qu=TP,=Z21Kq
q是图中三维点P经过T的变换后在第二帧图像的三维坐标,u就是其在第二帧图像对应的像素。接着也是一阶的泰勒展开:
∂
e
∂
T
=
∂
I
2
∂
u
∂
u
∂
q
∂
q
∂
δ
ξ
δ
ξ
\frac{\partial e}{\partial \boldsymbol{T}}=\frac{\partial \boldsymbol{I}_2}{\partial \boldsymbol{u}} \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{q}} \frac{\partial \boldsymbol{q}}{\partial \delta \boldsymbol{\xi}} \delta \boldsymbol{\xi}
∂T∂e=∂u∂I2∂q∂u∂δξ∂qδξ
最终可以得到:
J
=
−
∂
I
2
∂
u
∂
u
∂
δ
ξ
\boldsymbol{J}=-\frac{\partial \boldsymbol{I}_2}{\partial \boldsymbol{u}} \frac{\partial \boldsymbol{u}}{\partial \delta \boldsymbol{\xi}}
J=−∂u∂I2∂δξ∂u
其中
∂
u
∂
δ
ξ
=
[
f
x
Z
0
−
f
x
X
Z
2
−
f
x
X
Y
Z
2
f
x
+
f
x
X
2
Z
2
−
f
x
Y
Z
0
f
y
Z
−
f
y
Y
Z
2
−
f
y
−
f
y
Y
2
Z
2
f
y
X
Y
Z
2
f
y
X
Z
]
\frac{\partial \boldsymbol{u}}{\partial \delta \boldsymbol{\xi}}=\left[\begin{array}{cccccc}\frac{f_x}{Z} & 0 & -\frac{f_x X}{Z^2} & -\frac{f_x X Y}{Z^2} & f_x+\frac{f_x X^2}{Z^2} & -\frac{f_x Y}{Z} \\ 0 & \frac{f_y}{Z} & -\frac{f_y Y}{Z^2} & -f_y-\frac{f_y Y^2}{Z^2} & \frac{f_y X Y}{Z^2} & \frac{f_y X}{Z}\end{array}\right]
∂δξ∂u=[Zfx00Zfy−Z2fxX−Z2fyY−Z2fxXY−fy−Z2fyY2fx+Z2fxX2Z2fyXY−ZfxYZfyX]
是前面BA也涉及到的雅可比,经典像素对左扰动的雅可比。
代码实现
书中的代码也是给出了手动高斯牛顿的方法,并且结合图像金字塔。结果也是显然,多层直接发的误差最终是更小,效果也更好。
总结
光流法总结
本质上做了特征匹配的工作,光流法通过估计像素的运动来得到上一帧跟踪点在当前帧图像的像素位置。
优点:
- 运算速度快,因为省去了计算特征点描述子和特征匹配的过程
缺点:
- 灰度不变是很强的假设,实际并不一定满足,对图像的连续性和光照稳定性要求高
- 如果在一些角点很难提取的地方,像素点的跟踪效果会变差,导致后续位姿估计的结果
直接发总结
直接基于两帧图片,构建光度误差优化两帧图像之间的R和t。避免了跟踪点的过程。
优点:
- 直接法根据点的来源分成稀疏直接法,半稠密直接法,稠密直接法。一般稀疏直接法用于实时性要求高的视觉定位系统中。稠密直接法一般用于结构重建上。
- 稀疏直接法计算速度快,省去计算特征点和描述子的时间,实时性较好。
- 有像素梯度即可,不要求特征点,所以在一些特征缺失的场景可以使用。
缺点:
- 本质上图像是非凸函数,所以优化的过程中会容易陷入局部最优。可以通过图像金字塔改善效果。
- 直接法在选点少的情况下,效果不好,一般建议500个点以上。
- 灰度不变假设,实际不一定满足。



![BUUCTF靶场 [reverse]easyre、reverse1、reverse2](https://img-blog.csdnimg.cn/direct/9be86f9bde314d51a47f178dbdb83e83.png)


![分布式微服务之springboot学习[上]](https://img-blog.csdnimg.cn/direct/ffe0546968a448bda8f8f58b0b2bbe05.png)