🔥 个人主页：空白诗

🚀 引言

快速排序（Quick Sort）是一种高效的排序算法，由计算机科学界的传奇人物托尼·霍尔（Tony Hoare）于1960年巧妙地提出。这一算法的核心智慧在于运用了经典的分治法策略——犹如古代兵法中的“分而治之”，将一个错综复杂的大列表分割成两个相对简单的子列表，随后对这两个子列表施以同样的策略，直到每个子列表都只剩下单一元素或为空，此时整个序列自然归于有序。此过程宛如构建一座秩序井然的金字塔，自下而上，层层推进。

---

📌 快速排序算法核心思想

1. 选择基准值（Pivot）

这是算法流程的起点，从数列中精心挑选出一个元素，赋予它一个特殊角色——“基准”（pivot）。基准的选择可以很灵活，但理想情况下应倾向于选择一个能将数据集大致均匀分割的值，以促进算法效率。

2. 分区操作（Partitioning）

分区操作是快速排序的精髓所在。其目标是在遍历数列一次的过程中，通过交换元素位置，使得所有小于基准值的元素都位于基准之前，而所有大于基准值的元素都排列在其后，相等的元素可以放置在任一侧，完成这一操作后，基准值恰好位于其最终排序后的位置，即序列的中间。这一巧妙划分不仅为后续递归奠定了基础，也直接体现了快速排序分而治之的哲学。

3. 递归排序子序列

基于分区结果，数列被明确划分为两个独立的部分：左侧全部小于基准值，右侧则大于基准值。接下来，算法会对这两个子序列递归地应用同样的排序逻辑。通过不断地将问题规模减半，直到每个子序列只剩下一个或零个元素（这时自然视为已排序），整个数列便会在这一系列递归调用中逐步构建出全局的有序状态。这一策略确保了快速排序高效利用了分治策略的优势，尤其是在平均情况下展现出极高的效率。

---

📌 JavaScript 实现

1. 快速排序主函数

function quickSort(arr, left = 0, right = arr.length - 1) {
  // 如果左指针小于右指针，说明还有未排序的区间
  if (left < right) {
    // 调用分区函数，返回pivot的索引，完成一次分区
    const pivotIndex = partition(arr, left, right);
    
    // 对pivot左边的子数组进行快速排序
    quickSort(arr, left, pivotIndex - 1);
    // 对pivot右边的子数组进行快速排序
    quickSort(arr, pivotIndex + 1, right);
  }
  
  // 返回排序后的数组，实际上由于是原地排序，此处return并非必要
  return arr;
}

2. 分区函数

function partition(arr, left, right) {
  // 选择最右侧元素作为基准值pivot
  const pivot = arr[right];
  let i = left; // i为小于pivot的元素的边界，初始时指向最左侧
  
  // 遍历除了pivot外的所有元素
  for (let j = left; j < right; j++) {
    // 如果当前元素小于或等于pivot
    if (arr[j] <= pivot) {
      // 交换arr[i]和arr[j]，并将i右移一位，保持i左侧的元素都小于等于pivot
      [arr[i], arr[j]] = [arr[j], arr[i]]; // ES6解构赋值进行交换
      i++; 
    }
  }
  
  // 最后将pivot（arr[right]）与arr[i]交换，使得pivot位于正确的位置上
  [arr[i], arr[right]] = [arr[right], arr[i]];
  
  // 返回pivot的最终位置索引
  return i;
}

3. 示例代码

// 未排序数组示例
const unsortedArray = [3, 6, 8, 10, 1, 2, 1];

// 打印原始数组
console.log("Unsorted:", unsortedArray);

// 调用快速排序函数，得到排序后的数组
const sortedArray = quickSort(unsortedArray);

// 打印排序后的数组
console.log("Sorted:", sortedArray);

这段代码实现了快速排序算法，通过quickSort函数递归地将数组分为更小的子数组，并通过partition函数完成每部分的排序，最终达到整个数组有序的目的。代码中使用了ES6的解构赋值来简化元素交换的操作，使得代码更加简洁易读。

---

📌 优化建议

1. 三数取中法

• 核心思想：通过更智能地选择基准值(pivot)来优化快速排序的性能。
• 操作步骤：
  1. 比较数组首部、中部、尾部的元素。
  2. 选取这三个数中的中位数作为分区操作的基准值。
  3. 这样做能有效平衡划分，即使在数据部分有序的情况下也能保持较好的性能，减少最坏情况的发生概率。

2. 小数组时切换排序算法

• 适用条件：当待排序序列的元素数量较少时（例如少于10或15个）。
• 策略详情：快速排序在小数组上的优势不明显，此时切换到插入排序等简单排序算法更为高效。因为插入排序在小数据集上具有较低的常数因子和无需递归的优点，能够快速完成排序，与快速排序形成互补。

3. 尾递归优化

• 概念阐述：确保递归调用是函数的最后一个操作，便于某些支持该特性的编译器进行优化。
• 实施方法：设计递归逻辑时，直接在递归调用的返回语句中返回计算结果，避免在递归返回后还需执行其他操作。
• 注意事项：虽然JavaScript等语言不一定能自动优化尾递归，遵循此原则编写代码依然有助于提高可读性和未来跨平台移植的兼容性。

4. 并行化处理

• 目标：利用多核CPU资源加速排序过程。
• 实施步骤：
  1. 将大数组分割成多个小块。
  2. 各个CPU核心独立并行地对分块数据执行快速排序。
  3. 最后合并各块已排序的结果。
• 优势：在拥有多个处理器核心的系统上，此策略能显著缩短排序时间，尤其适合处理海量数据。

通过上述一系列优化措施，快速排序算法不仅在理论上保持了较高的时间效率，在实际应用中也变得更加灵活和健壮，能够有效应对各种规模数据集的排序挑战，展现出更高的性能和稳定性。

---

📌 时间复杂度分析

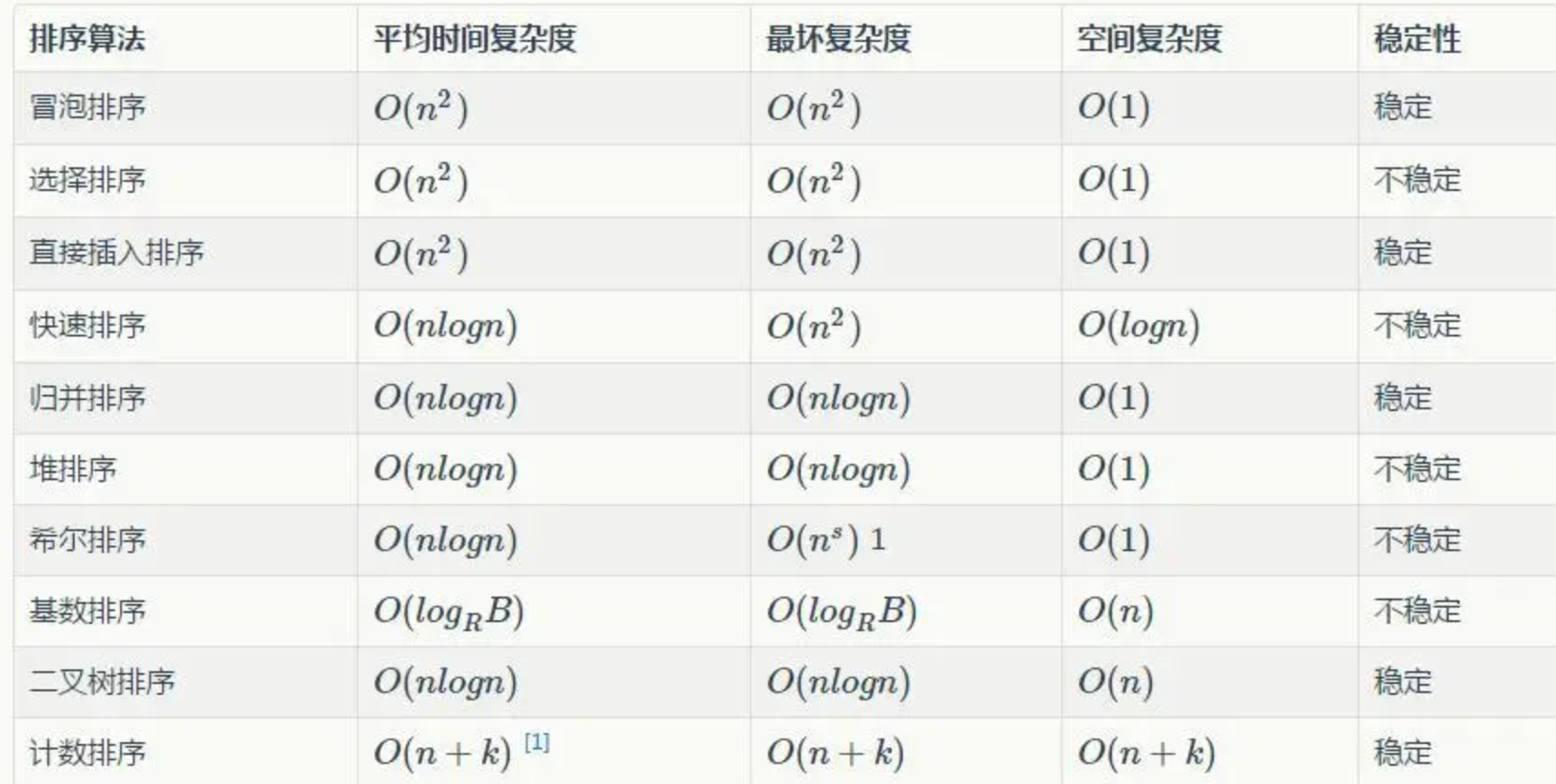
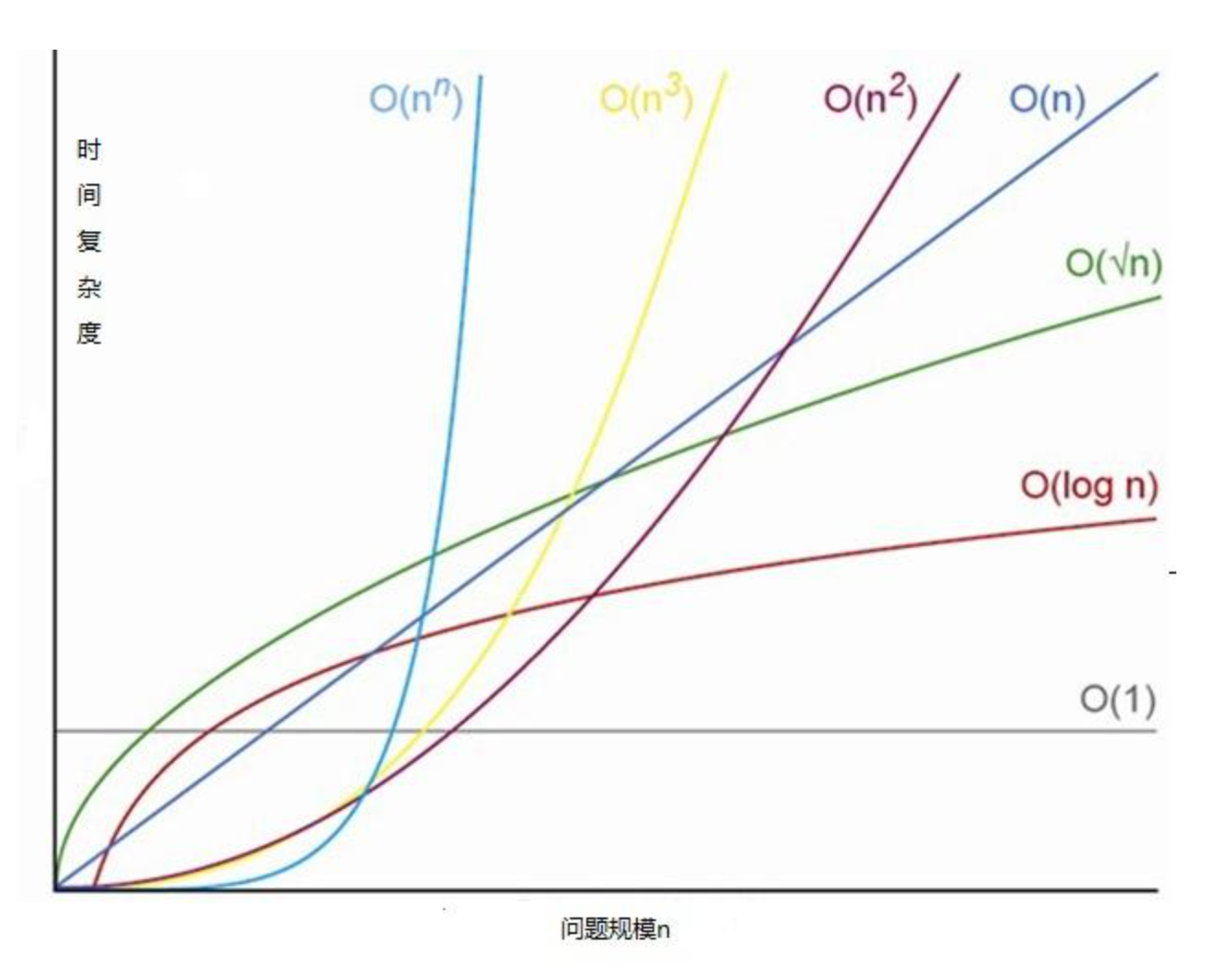
快速排序算法的性能极大程度上取决于基准值（Pivot）的选择策略。

• 最优情况：若每次分区操作都能均匀地将数据集切分为两部分，每部分包含近似相等数量的元素，则递归树的深度为log₂n。鉴于每一层递归涉及遍历数组，总体操作计数约为n * log₂n。因此，快速排序在最佳情况下的时间复杂度为O(n log n)，表现出高度的效率。

• 最差情况：相反，若每次选取的基准值都导致极不均衡的分区，极端情形下每次仅将数组分为一个元素和剩余所有元素两部分，这将导致递归深度上升至n，伴随每次遍历数组的操作，时间复杂度恶化为O(n²)，与冒泡排序相近。

• 平均情况：在实践中，若假定分区大致均匀，即每次都能将数据集分为两个大小相似的子集，快速排序的平均时间复杂度同样为O(n log n)。这对于多数随机分布数据集而言，是一个非常高效的排序方案。

鉴于最坏情况下的性能瓶颈，实际部署快速排序算法时，往往配合采用基准值优化策略，比如“三数取中法”，来增强其鲁棒性和普遍适用性，确保在多种数据条件下仍能保持高效的排序性能。

---

📌 总结

快速排序算法通过分治法策略实现高效排序，其核心包括选择基准值、分区操作及递归排序子序列三大步骤。为了进一步提升性能和适应不同场景，可采纳诸如三数取中法优化基准选择、小数组时切换至插入排序、尾递归优化及并行处理等策略。这些优化不仅能够减少最坏情况出现的概率，还充分利用现代计算资源，使快速排序在实践中表现得更为出色，成为处理大量数据排序任务的优选算法之一。

总之，快速排序凭借其高效与灵活性，在众多排序算法中占据重要地位，广泛应用于各种数据排序需求之中。

---