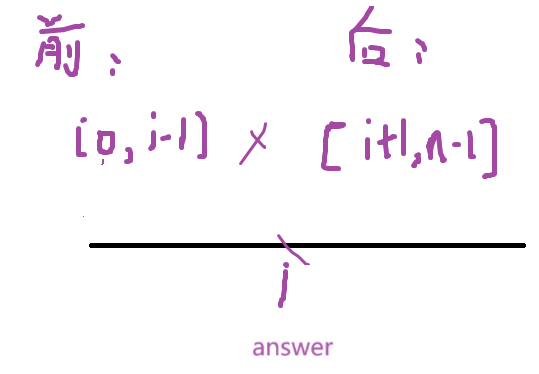A 两个字符串的排列差

模拟:遍历 s s s 记录各字符出现的位置,然后遍历 t t t 计算排列差
class Solution {
public:
int findPermutationDifference(string s, string t) {
int n = s.size();
vector<int> loc(26);
for (int i = 0; i < n; i++)
loc[s[i] - 'a'] = i;
int res = 0;
for (int i = 0; i < n; i++)
res += abs(loc[t[i] - 'a'] - i);
return res;
}
};
B 从魔法师身上吸取的最大能量

模拟:设 p [ i ] p[i] p[i] 为从 i i i 出发能获得的最大能量,逆序遍历 e n e r g y energy energy 求 p p p
class Solution {
public:
int maximumEnergy(vector<int>& energy, int k) {
int n = energy.size();
vector<int> p(n);
for (int i = n - 1; i >= 0; i--)
p[i] = i + k < n ? p[i + k] + energy[i] : energy[i];
return *max_element(p.begin(), p.end());
}
};
C 矩阵中的最大得分

前缀极值:可以发现一条移动路径的得分只和路径的终点和起点有关,所以当终点固定为 g r i d [ i ] [ j ] grid[i][j] grid[i][j] 时,起点值为 g r i d [ 0 , i ] [ 0 , j ] grid[0,i][0,j] grid[0,i][0,j] 中非 g r i d [ i ] [ j ] grid[i][j] grid[i][j] 的最小值时得分最大。所以枚举终点,用二维前缀维护子矩阵中非 g r i d [ i ] [ j ] grid[i][j] grid[i][j] 的最小值。
class Solution {
public:
int maxScore(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int mn[m][n];
int res = INT32_MIN;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
if (i == 0) {
mn[i][j] = j == 0 ? grid[i][j] : min(mn[i][j - 1], grid[i][j]);
if (j != 0)
res = max(res, grid[i][j] - mn[i][j - 1]);
} else {
mn[i][j] = j == 0 ? min(mn[i - 1][j], grid[i][j]) : min({mn[i - 1][j], mn[i][j - 1], grid[i][j]});
if (j != 0)
res = max(res, grid[i][j] - min(mn[i - 1][j], mn[i][j - 1]));
else
res = max(res, grid[i][j] - mn[i - 1][j]);
}
}
return res;
}
};
D 找出分数最低的排列
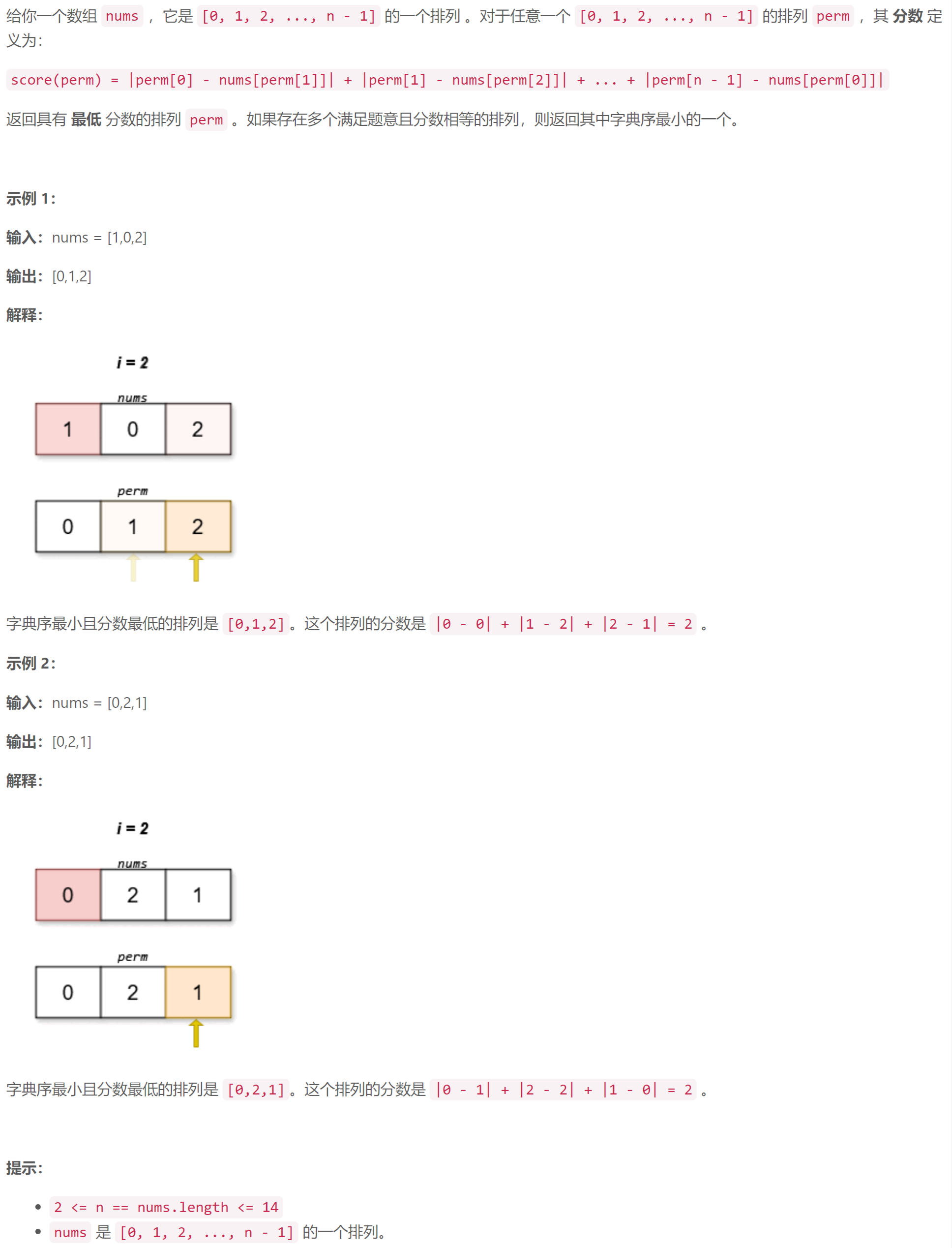
状态压缩:根据分数计算公式,有一个重要的结论是:把 p e r m perm perm 看成一个环,在环上选择不同位置作为数组起点可以得到不同的 p e r m perm perm 数组,但这些 p e r m perm perm 数组的分数是相同的,所以要想字典序最小, p e r m perm perm 首位为 0 0 0 。设 p [ c u r ] [ p i ] p[cur][pi] p[cur][pi] 为“当前各数的使用状态为 c u r cur cur (若 c u r > > i & 1 cur>>i\&1 cur>>i&1 则 i i i 已使用), p e r m perm perm 下一位为 p i pi pi ”的情况下,接下来能够获得的最大得分。通过记忆化搜索实现状态转移求 p [ 0 ] [ 0 ] p[0][0] p[0][0] , 同时用数组间接记录状态转移的路径。
class Solution {
public:
vector<int> findPermutation(vector<int>& nums) {
int n = nums.size();
int N = 1 << n;
vector<vector<int>> p(N, vector<int>(n, -1));//-1:初始化标志
vector<vector<int>> select(N, vector<int>(n, -1));//数组间接记录状态转移的路径
function<int(int, int, int)> get = [&](int cur, int pi, int ind) {
if (p[cur][pi] != -1)
return p[cur][pi];
if (ind == n - 1)//pi为perm的最后一个元素
return p[cur][pi] = abs(pi - nums[0]);
p[cur][pi] = INT32_MAX;
for (int np = 0; np < n; np++)
if ((cur >> np & 1) == 0 && np != pi)//枚举perm中pi的后一个元素np
if (abs(pi - nums[np]) + get(cur | (1 << pi), np, ind + 1) < p[cur][pi]) {
p[cur][pi] = abs(pi - nums[np]) + get(cur | (1 << pi), np, ind + 1);
select[cur][pi] = np;//记录路径
}
return p[cur][pi];
};
get(0, 0, 0);
vector<int> res;
int new_mask, new_cur;
for (int cur = 0, mask = 0; res.size() < n; mask = new_mask, cur = new_cur) {//重现路径
res.push_back(cur);
new_mask = mask | (1 << cur);
new_cur = select[mask][cur];
}
return res;
}
};