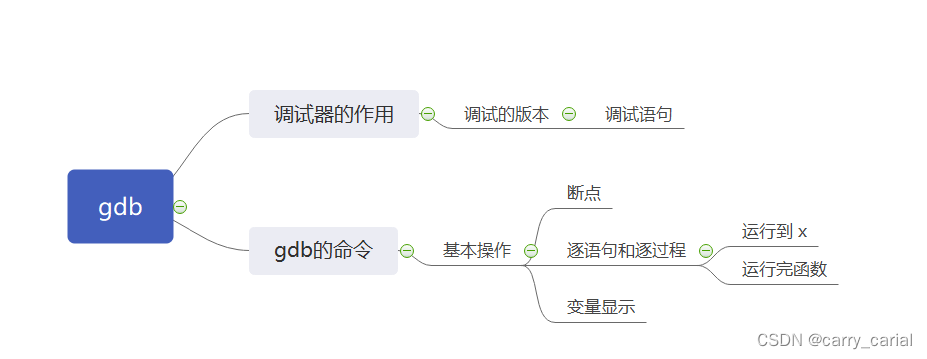
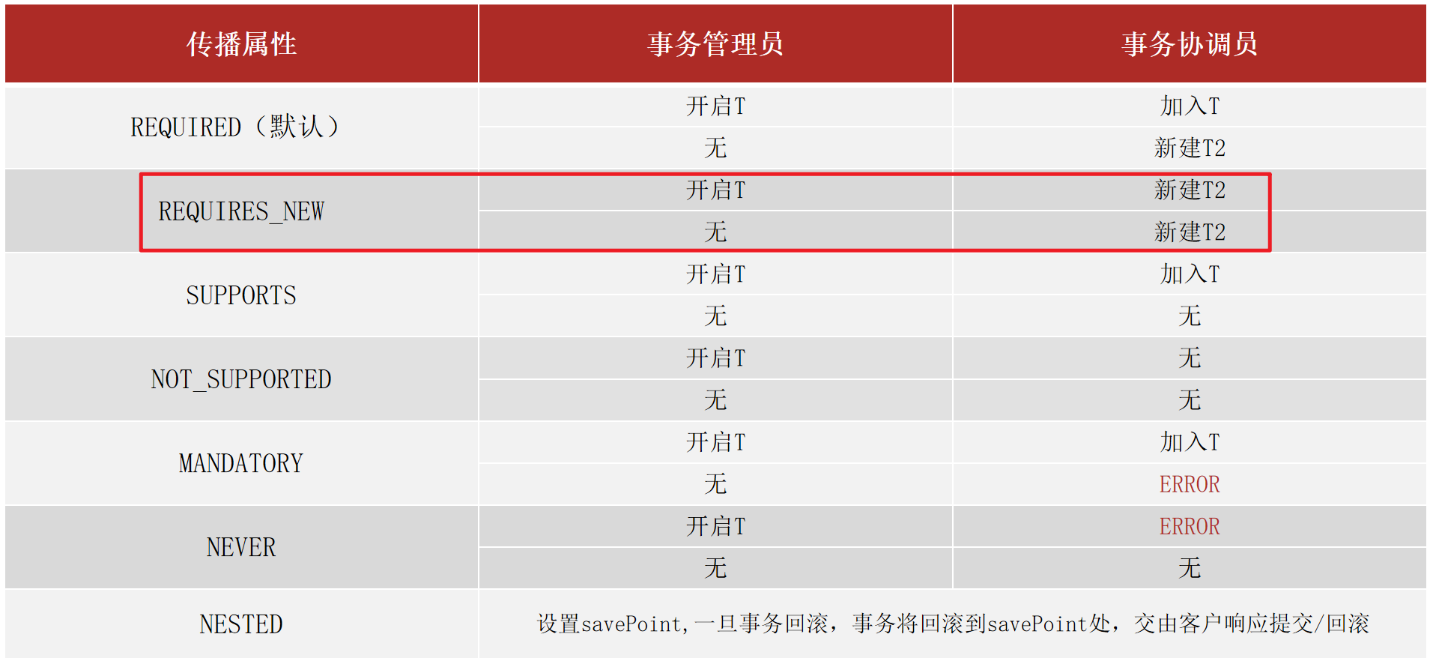
基于有向图的邻接矩阵计算其割点、割边、压缩图,并用networkx可视化绘制
- 为什么基于邻接矩阵计算图的割点、割边、压缩图
- 实现python代码
- 代码运行效果
- 结论:
为什么基于邻接矩阵计算图的割点、割边、压缩图
由于矩阵计算过程,被广泛优化;
因此,采用矩阵计算方法实施割点、割边、压缩图的计算,效率高、逻辑简单。
实现python代码
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from networkx.drawing.nx_agraph import graphviz_layout
# 有向图的邻接矩阵
M = np.array([
#1, 2, 3, 4, 5, 6, 7, 8
[0, 0, 0, 0, 0, 1, 0, 0], #u1->u6
[0, 0, 0, 0, 1, 0, 0, 0], #u2->u5
[0, 1, 0, 1, 0, 0, 0, 0], #u3->u2, u3->u4
[0, 0, 0, 0, 0, 0, 0, 1], #u4->u8
[0, 1, 1, 0, 0, 0, 0, 0], #u5->u2, u5->u3
[0, 0, 0, 0, 0, 0, 1, 0], #u6->u7
[0, 0, 0, 1, 0, 0, 0, 0], #u7->u4
[0, 0, 0, 0, 0, 1, 0, 0] #u8->u6
], int)
print('邻接矩阵:\n', M)
nVerts = M.shape[0] #顶点个数
# IM = I(单位阵) + M(邻接矩阵)————在邻接矩阵基础上,添加自环结构
IM = np.identity(nVerts, int) + M
# R = ((I + M) ** (n-1) == 1).astype(int),构造可达矩阵
# 矩阵的n次幂——矩阵连乘n次
R = (np.linalg.matrix_power(IM, nVerts - 1) > 0).astype(int)
print('可达矩阵:\n', R)
# 由R * R.T保持对称边,去除非对称边
sR = R * R.T
print('对称矩阵:\n', sR)
# 按对称矩阵sR中的行数据实施分组汇总
rows = [ [''.join(sR[i, :].astype(str)), i] for i in range(nVerts) ]
print('行数组编码组=\n', rows)
grps = {}
for row in rows:
if row[0] in grps.keys():
grps[row[0]].append( row[1])
else:
grps[row[0]] = [row[1]]
print('按相同编码实施顶点分组结果:\n', grps )
# 计算分组数量
nGroups = len(list(grps.keys()))
print('分组数量=', nGroups)
groupInfo = list(grps.values())
groups = {}
for grpNo, elems in enumerate(groupInfo):
for elem in elems:
groups[elem] = grpNo
print('按强连通特性分组的节点组:\n', groups)
# 压缩图的邻接矩阵
compactR = np.zeros((nGroups, nGroups))
# 遍历邻接矩阵获取组建连接信息
connGroups = {}
for i in range(nVerts):
for j in range(nVerts):
if i == j: continue #相同顶点关系继续
if groups[i] == groups[j]: continue #同组关系继续
if M[i, j] == 1:
compactR[groups[i], groups[j]] = 1 #记录压缩图中的组间有向边
cn = (groups[i], groups[j]) #不同组间的连接关系
if cn in connGroups.keys():
connGroups[cn] += [(i, j)]
else:
connGroups[cn] = [(i, j)]
print('组间连接关系=\n', connGroups)
# 根据组间连接关系获取候选割点、割边集合
cutEdges = [] #割边
cutVerts = [] #割点
for key in connGroups.keys():
vals = connGroups[key]
if len(vals) == 1:
print('割边', vals)
cutEdges += vals #添加割边
cutVerts += vals[0] #添加割点
# 根据邻接矩阵计算每个顶点的度数——为真实割点判断提供依据
# 顶点度数=行求和(出度)+ 列求和(入度)
vertDegrees = [np.sum(M[i, :]) + np.sum(M[:, i]) for i in range(nVerts)]
print('顶点度数=\n', vertDegrees)
print('候选割点=\n', cutVerts)
# 筛选掉度=1的候选割点————条件:割点的度数必须 > 1
cutVerts = [v for v in cutVerts if vertDegrees[v] > 1]
print('割点\n', cutVerts)
# 绘图
plt.figure()
plt.title('Directed graph')
dg = nx.DiGraph() #构造有向图
for i in range(nVerts):
for j in range(nVerts):
if M[i, j] == 1:
dg.add_edge(i, j) #添加有向边
# 智能布局节点位置
pos = graphviz_layout(dg, prog='dot')
nx.draw(dg, with_labels = True, pos = pos) #绘制有向图
# 绘制红色割边
nx.draw_networkx_edges(dg, pos = pos, edgelist=cutEdges, width=1.0, edge_color='r')
# 绘制红色割点
nx.draw_networkx_nodes(dg, pos = pos, nodelist=cutVerts, node_color='r')
plt.show()
# 根据压缩图的邻接矩阵,可绘图压缩图
plt.figure()
plt.title('compact graph')
dg1 = nx.DiGraph()
for i in range(nGroups):
for j in range(nGroups):
if compactR[i, j] == 1:
dg1.add_edge(i, j)
pos1 = graphviz_layout(dg1, prog='dot')
nx.draw(dg1, with_labels = True, pos = pos) #绘制有向图
plt.show()
代码运行效果
邻接矩阵:
[[0 0 0 0 0 1 0 0]
[0 0 0 0 1 0 0 0]
[0 1 0 1 0 0 0 0]
[0 0 0 0 0 0 0 1]
[0 1 1 0 0 0 0 0]
[0 0 0 0 0 0 1 0]
[0 0 0 1 0 0 0 0]
[0 0 0 0 0 1 0 0]]
可达矩阵:
[[1 0 0 1 0 1 1 1]
[0 1 1 1 1 1 1 1]
[0 1 1 1 1 1 1 1]
[0 0 0 1 0 1 1 1]
[0 1 1 1 1 1 1 1]
[0 0 0 1 0 1 1 1]
[0 0 0 1 0 1 1 1]
[0 0 0 1 0 1 1 1]]
对称矩阵:
[[1 0 0 0 0 0 0 0]
[0 1 1 0 1 0 0 0]
[0 1 1 0 1 0 0 0]
[0 0 0 1 0 1 1 1]
[0 1 1 0 1 0 0 0]
[0 0 0 1 0 1 1 1]
[0 0 0 1 0 1 1 1]
[0 0 0 1 0 1 1 1]]
行数组编码组=
[[‘10000000’, 0], [‘01101000’, 1], [‘01101000’, 2], [‘00010111’, 3], [‘01101000’, 4], [‘00010111’, 5], [‘00010111’, 6], [‘00010111’, 7]]
按相同编码实施顶点分组结果:
{‘10000000’: [0], ‘01101000’: [1, 2, 4], ‘00010111’: [3, 5, 6, 7]}
分组数量= 3
按强连通特性分组的节点组:
{0: 0, 1: 1, 2: 1, 4: 1, 3: 2, 5: 2, 6: 2, 7: 2}
组间连接关系=
{(0, 2): [(0, 5)], (1, 2): [(2, 3)]}
割边 [(0, 5)]
割边 [(2, 3)]
顶点度数=
[1, 3, 3, 3, 3, 3, 2, 2]
候选割点=
[0, 5, 2, 3]
割点
[5, 2, 3]
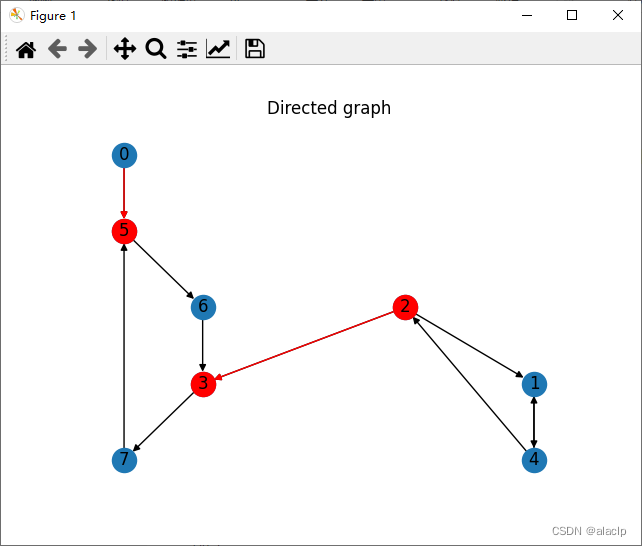
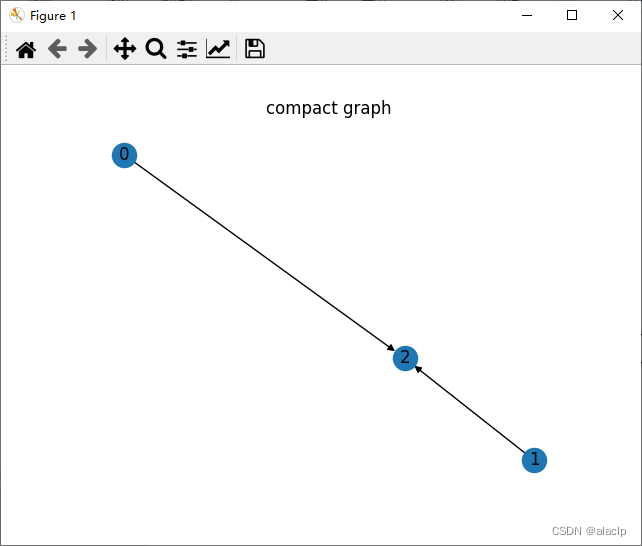
结论:
图(graph),是表达对象关系的有效方法;
而针对复杂图的分析,由于结构多变,故用程序逻辑法求解的话,难以编程。
通过使用矩阵计算方法,获取图中的相关信息,对于图分析可起到简捷、高效的作用。