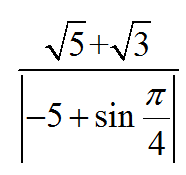简介
主页:https://hojonathanho.github.io/diffusion/
扩散模型 (diffusion models)是深度生成模型中新的SOTA。
扩散模型在图片生成任务中超越了原SOTA:GAN,并且在诸多应用领域都有出色的表现,如计算机视觉,NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化等。
GAN要训练两个网络,训练难度大,容易不收敛,而且多样性比较差,毕竟生成器是为了骗过鉴别器,生成器可能学到稀奇古怪的技巧,
此外,扩散模型与其他研究领域有着密切的联系,如稳健学习、表示学习、强化学习。
然而,原始的扩散模型也有缺点,它的采样速度慢,通常需要数千个评估步骤才能抽取一个样本;它的最大似然估计无法和基于似然的模型相比;它泛化到各种数据类型的能力较差。
如今很多研究已经从实际应用的角度解决上述限制做出了许多努力,或从理论角度对模型能力进行了分析。但是,现在仍缺乏对扩散模型从算法到应用的最新进展的系统回顾。
实现流程
生成式建模的一个核心问题是模型的灵活性和可计算性之间的权衡。
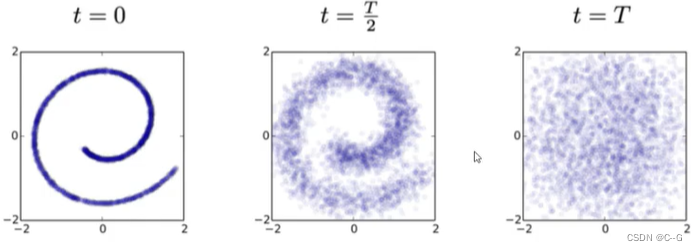
扩散模型的基本思想是正向扩散过程来系统地扰动数据中的分布,然后通过学习反向扩散过程恢复数据的分布,这样就了产生一个高度灵活且易于计算的生成模型。
前向过程

前向过程概括起来就是从原始图像
X
0
X_0
X0 开始,不断往图像中加入高斯噪声,每一个时刻由前一时刻的图像增加噪声得到,最后得到纯噪声的图像。这个过程可以看作是不断构建标签(高斯噪声)的过程。
构建 X t X_t Xt 时刻是公式如下:
X t = α t X t − 1 + 1 − α t Z X_t = \sqrt{\alpha_t} X_{t-1} + \sqrt{1-\alpha_t}Z Xt=αtXt−1+1−αtZ
其中 α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt
β \beta β 随着时刻 t 增大而增加,论文从0.0001 增加到 0.002。那么 α \alpha α 随着时刻 t 增大而减少,这表明了后一时刻的图像对前一时刻的图像的依赖逐渐减少,高斯噪声的权重逐渐增大,最后得到纯噪声的图像
从公式中,我们可以从时刻0 X 0 X_0 X0 一步一步往后推,可以得到限定时刻 X t X_t Xt,在这个过程中我们要存储每一时刻的 α \alpha α 和 高斯噪声 Z Z Z
我们现在可以实现加噪声的过程了,但是目的是去噪生成,也就是接下来的逆向过程
逆向过程
那么我们回到我们的初始目的,如何从 T N T_N TN 时刻纯噪声图像生成目标图像呢?接下来尝试从 T N T_N TN 往前推导,以得到 T 0 T_0 T0 时刻的图像
首先,时刻 t 的图像记为 X t X_t Xt,前一时刻 t-1 的图像记为 X t − 1 X_{t-1} Xt−1,这里使用 Z 表示高斯分布
已知,
X
t
=
α
t
X
t
−
1
+
1
−
α
t
Z
X_t = \sqrt{\alpha_t} X_{t-1} + \sqrt{1-\alpha_t}Z
Xt=αtXt−1+1−αtZ
将
X
t
−
1
=
α
t
−
1
X
t
−
2
+
1
−
α
t
−
1
Z
X_{t-1} = \sqrt{\alpha_{t-1}} X_{t-2} + \sqrt{1-\alpha_{t-1}}Z
Xt−1=αt−1Xt−2+1−αt−1Z 代入上述公式,取代
X
t
−
1
X_{t-1}
Xt−1,得到
X t = α t ( α t − 1 X t − 2 + 1 − α t − 1 Z ) + 1 − α t Z X_t = \sqrt{\alpha_t} (\sqrt{\alpha_{t-1}} X_{t-2} + \sqrt{1-\alpha_{t-1}}Z) + \sqrt{1-\alpha_t}Z Xt=αt(αt−1Xt−2+1−αt−1Z)+1−αtZ
化简得
X t = α t α t − 1 X t − 2 + α t − α t α t − 1 Z + 1 − α t Z X_t = \sqrt{\alpha_t \alpha_{t-1}} X_{t-2} + \sqrt{\alpha_t-\alpha_t\alpha_{t-1}}Z + \sqrt{1-\alpha_t}Z Xt=αtαt−1Xt−2+αt−αtαt−1Z+1−αtZ
由于每次加入的噪声都服从高斯分布 Z ∼ N ( 0 , I ) Z \sim \Nu(0,I) Z∼N(0,I)
α t − α t α t − 1 Z ∼ N ( 0 , α t − α t α t − 1 ) \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}Z \sim \Nu(0,\alpha_t - \alpha_t\alpha_{t-1}) αt−αtαt−1Z∼N(0,αt−αtαt−1)
1 − α t Z ∼ N ( 0 , 1 − α t ) \sqrt{1-\alpha_t}Z \sim \Nu(0,1-\alpha_t) 1−αtZ∼N(0,1−αt)
由于高斯分布符合以下规律
N ( 0 , σ 1 2 I ) + N ( 0 , σ 2 2 I ) ∼ N ( 0 , ( σ 1 2 + σ 2 2 ) I ) \Nu(0,\sigma^2_1 I) + \Nu(0,\sigma^2_2 I) \sim \Nu(0,(\sigma^2_1 + \sigma^2_2)I) N(0,σ12I)+N(0,σ22I)∼N(0,(σ12+σ22)I)
所以
α t − α t α t − 1 Z + 1 − α t Z ∼ N ( 0 , 1 − α t α t − 1 ) \sqrt{\alpha_t-\alpha_t\alpha_{t-1}}Z + \sqrt{1-\alpha_t}Z\sim \Nu(0,1-\alpha_t\alpha_{t-1}) αt−αtαt−1Z+1−αtZ∼N(0,1−αtαt−1)
原式
X t = α t α t − 1 X t − 2 + α t − α t α t − 1 Z + 1 − α t Z X_t = \sqrt{\alpha_t \alpha_{t-1}} X_{t-2} + \sqrt{\alpha_t-\alpha_t\alpha_{t-1}}Z + \sqrt{1-\alpha_t}Z Xt=αtαt−1Xt−2+αt−αtαt−1Z+1−αtZ
化简可得
X t = α t α t − 1 X t − 2 + 1 − α t α t − 1 Z X_t = \sqrt{\alpha_t \alpha_{t-1}} X_{t-2} + \sqrt{1-\alpha_t\alpha_{t-1}} Z Xt=αtαt−1Xt−2+1−αtαt−1Z
从而可以推出
X t = α ˉ X 0 + 1 − α ˉ Z X_t = \sqrt{ \bar{\alpha}} X_0 + \sqrt{1-\bar{\alpha}} Z Xt=αˉX0+1−αˉZ,( α ˉ \bar{\alpha} αˉ 表示连乘)
从该公式可以看出,任意时刻的分布都可以通过 X 0 X_0 X0 这个初始状态算出来,唯一不确定的因素是噪声
那么一步步往前迭代,让神经网络去预测每一时刻的噪声 Z Z Z,那么在强约束的条件下,理论上就可以得到目标图像
回到原始公式
X t = α t X t − 1 + 1 − α t Z X_t = \sqrt{\alpha_t} X_{t-1} + \sqrt{1-\alpha_t}Z Xt=αtXt−1+1−αtZ
那么我们要如何使用 X t X_t Xt 表示 X t − 1 X_{t-1} Xt−1呢
这里使用贝叶斯公式
q ( X t − 1 ∣ X t ) = q ( X t ∣ X t − 1 ) q ( X t − 1 ) q ( X t ) q(X_{t-1}|X_t) = q(X_t|X_{t-1}) \frac{q(X_{t-1})}{q(X_t)} q(Xt−1∣Xt)=q(Xt∣Xt−1)q(Xt)q(Xt−1)
由于我们只知道初始条件 X 0 X_0 X0,那么根据上面的推导,可以使用 X 0 X_0 X0 表示任意时刻 X t X_t Xt
X t = α ˉ X 0 + 1 − α ˉ Z X_t = \sqrt{ \bar{\alpha}} X_0 + \sqrt{1-\bar{\alpha}} Z Xt=αˉX0+1−αˉZ,( α ˉ \bar{\alpha} αˉ 表示连乘)
那么套用贝叶斯的原始公式可以使用初始条件 X 0 X_0 X0 表示
q ( X t − 1 ∣ X t , X 0 ) = q ( X t ∣ X t − 1 , X 0 ) q ( X t − 1 ∣ X 0 ) q ( X t ∣ X 0 ) q(X_{t-1}|X_t,X_0) = q(X_t|X_{t-1},X_0) \frac{q(X_{t-1} | X_0)}{q(X_t | X_0)} q(Xt−1∣Xt,X0)=q(Xt∣Xt−1,X0)q(Xt∣X0)q(Xt−1∣X0)
右边三项未知数可以表示为:
q ( X t − 1 ∣ X 0 ) : α ˉ t − 1 X 0 + 1 − α ˉ t − 1 Z ∼ N ( α ˉ t − 1 X 0 , 1 − α ˉ t − 1 ) q(X_{t-1} | X_0) : \sqrt{\bar{\alpha}_{t-1}}X_0 + \sqrt{1-\bar{\alpha}_{t-1}}Z \sim \Nu(\sqrt{\bar{\alpha}_{t-1}}X_0,1-\bar{\alpha}_{t-1}) q(Xt−1∣X0):αˉt−1X0+1−αˉt−1Z∼N(αˉt−1X0,1−αˉt−1)
q ( X t ∣ X 0 ) : α ˉ t X 0 + 1 − α ˉ t Z ∼ N ( α ˉ t X 0 , 1 − α ˉ t ) q(X_{t} | X_0) : \sqrt{\bar{\alpha}_{t}}X_0 + \sqrt{1-\bar{\alpha}_{t}}Z \sim \Nu(\sqrt{\bar{\alpha}_{t}}X_0,1-\bar{\alpha}_{t}) q(Xt∣X0):αˉtX0+1−αˉtZ∼N(αˉtX0,1−αˉt)
q ( X t ∣ X t − 1 , X 0 ) : α t X t − 1 + 1 − α t Z ∼ N ( α t X t − 1 , 1 − α t ) q(X_{t} | X_{t-1} , X_0) : \sqrt{\alpha_t} X_{t-1} + \sqrt{1-\alpha_t}Z \sim \Nu(\sqrt{{\alpha}_{t}}X_{t-1},1-{\alpha}_{t}) q(Xt∣Xt−1,X0):αtXt−1+1−αtZ∼N(αtXt−1,1−αt)
将上面三条公式带入
q ( X t − 1 ∣ X t , X 0 ) = q ( X t ∣ X t − 1 , X 0 ) q ( X t − 1 ∣ X 0 ) q ( X t ∣ X 0 ) q(X_{t-1}|X_t,X_0) = q(X_t|X_{t-1},X_0) \frac{q(X_{t-1} | X_0)}{q(X_t | X_0)} q(Xt−1∣Xt,X0)=q(Xt∣Xt−1,X0)q(Xt∣X0)q(Xt−1∣X0)
其中 Z = e − 1 2 ( x − μ ) 2 σ 2 Z = e^{-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}} Z=e−21σ2(x−μ)2
化简得到
X t − 1 = e ( − 1 2 ( ( x t − α t X t − 1 ) 2 β t + ( X t − 1 − α ˉ t − 1 X 0 ) 2 1 − α ˉ t − 1 − ( X t − α ˉ t X 0 ) 2 1 − α ˉ t ) ) X_{t-1} = e^{ (-\frac{1}{2} ( \frac{(x_t - \sqrt{\alpha_t} X_{t-1})^2}{\beta_t} +\frac{(X_{t-1} - \sqrt{\bar{\alpha}_{t-1}}X_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(X_t-\sqrt{\bar{\alpha}_t}X_0)^2}{1-\bar{\alpha}_t} ))} Xt−1=e(−21(βt(xt−αtXt−1)2+1−αˉt−1(Xt−1−αˉt−1X0)2−1−αˉt(Xt−αˉtX0)2))
将标准正太分布展开后,汇总化简得到
e ( − 1 2 ( ( α t β t + 1 1 − α ˉ t − 1 ) X t − 1 2 − ( 2 α t β t X t + 2 α ˉ t − 1 1 − α ˉ t − 1 X 0 ) X t − 1 + C ( X t , X 0 ) ) ) e^{( -\frac{1}{2} ( (\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}} ) X^2_{t-1} - ( \frac{2\sqrt{\alpha_t}}{\beta_t}X_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}X_0 )X_{t-1} +C(X_t,X_0) ) )} e(−21((βtαt+1−αˉt−11)Xt−12−(βt2αtXt+1−αˉt−12αˉt−1X0)Xt−1+C(Xt,X0)))
C ( X t , X 0 ) C(X_t,X_0) C(Xt,X0) 为常数项,不影响任务,核心是球 X t X_t Xt 与 X t − 1 X_{t-1} Xt−1 的关系。
将高斯分布(Z) 展开后为
Z = e ( − ( x − μ ) 2 2 σ 2 ) = e ( − 1 2 ( 1 σ 2 X 2 − 2 μ σ 2 X + μ 2 σ 2 ) ) Z = e^{(-\frac{ (x-\mu)^2 }{2\sigma^2})} = e^{ (-\frac{1}{2} ( \frac{1}{\sigma^2}X^2 - \frac{2\mu}{\sigma^2}X + \frac{\mu^2}{\sigma^2} ) ) } Z=e(−2σ2(x−μ)2)=e(−21(σ21X2−σ22μX+σ2μ2))
对比 高斯分布(Z) 展开后公式 与 上述得到的
X
t
−
1
X_{t-1}
Xt−1 表达式,可以得到均值 和 方差
1
σ
2
=
(
α
t
β
t
+
1
1
−
α
ˉ
t
−
1
)
\frac{1}{\sigma^2} =(\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}} )
σ21=(βtαt+1−αˉt−11)
σ = α t ( 1 − α ˉ t − 1 ) + β t β t ( 1 − α ˉ t − 1 ) \sigma = \sqrt{ \frac{ \alpha_t(1-\bar{\alpha}_{t-1}) + \beta_t }{ \beta_t(1- \bar{\alpha}_{t-1}) } } σ=βt(1−αˉt−1)αt(1−αˉt−1)+βt
μ ~ ( X t , X 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t X t + α ˉ t − 1 β t 1 − α ˉ t X 0 \tilde{\mu}(X_t,X_0) = \frac{\sqrt{\alpha}_t (1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}X_t + \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t}X_0 μ~(Xt,X0)=1−αˉtαt(1−αˉt−1)Xt+1−αˉtαˉt−1βtX0
其中 X 0 X_0 X0 未知,但是我们知道 X t X_t Xt 可以由 X 0 X_0 X0 得到,那么将原公式逆过来
X t = α ˉ X 0 + 1 − α ˉ Z X_t = \sqrt{ \bar{\alpha}} X_0 + \sqrt{1-\bar{\alpha}} Z Xt=αˉX0+1−αˉZ,( α ˉ \bar{\alpha} αˉ 表示连乘)
X 0 = 1 α ˉ t ( X t − 1 − α ˉ t Z ) X_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} (X_t - \sqrt{1-\bar{\alpha}_t} Z) X0=αˉt1(Xt−1−αˉtZ)
再将 X 0 X_0 X0 带入均值表达式,化简得
μ ~ t = 1 α t ( X t − β t 1 − α ˉ t Z ) \tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} (X_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}Z) μ~t=αt1(Xt−1−αˉtβtZ)
每一时刻的 X t X_t Xt 都是一个高斯分布,因此,高斯分布重采样策略得到 X t − 1 X_{t-1} Xt−1
我们现在得到了有样本 X 得到的分布 X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2)。采样这个操作本身是不可导的,但是我们可以通过重参数化技巧,将简单分布的采样结果变换到特定分布中,如此一来则可以对变换过程进行求导。具体而言,我们从标准高斯分布中采样,并将其变换到 X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2),过程如下
ε
∼
N
(
0
,
I
)
\varepsilon \sim \Nu(0,I)
ε∼N(0,I)
Z
=
μ
+
σ
×
ε
Z = \mu + \sigma \times \varepsilon
Z=μ+σ×ε
也就是说,从 N ( μ , σ 2 ) \Nu(\mu,\sigma^2) N(μ,σ2) 采样 Z Z Z,等同于从 ε ∼ N ( 0 , I ) \varepsilon \sim \Nu(0,I) ε∼N(0,I) 中采样高斯噪声 ε \varepsilon ε,再将其按 Z = μ + σ × ε Z = \mu + \sigma \times \varepsilon Z=μ+σ×ε 变换
X t − 1 = μ ~ t + σ t Z ∼ N ( μ ~ t , σ t ) X_{t-1} = \tilde{\mu}_t + \sigma_tZ \sim \Nu(\tilde{\mu}_t,\sigma_t) Xt−1=μ~t+σtZ∼N(μ~t,σt)
伪代码
总体网络可以采用了简单的U-net实现
Training
目标:让网络预测不同时刻的高斯分布
ε
θ
\varepsilon_\theta
εθ

首先从数据集中随机采样图像
X
0
X_0
X0,选取超参数时刻上限
T
T
T,在
1
,
.
.
.
,
T
1,...,T
1,...,T 中随机采样时刻(batch size)并为此生成时刻对应的高斯分布
ε
\varepsilon
ε,根据公式
X t = α ˉ X 0 + 1 − α ˉ Z X_t = \sqrt{ \bar{\alpha}} X_0 + \sqrt{1-\bar{\alpha}} Z Xt=αˉX0+1−αˉZ,( α ˉ \bar{\alpha} αˉ 表示连乘)
将 t 时刻的分布 X t X_t Xt 和时刻 t 输入网络,其中时刻 t 经过位置编码后与 X t X_t Xt 拼接,网络预测得到时刻 t 的高斯分布 ε θ \varepsilon_\theta εθ,将其与对应时刻的高斯分布 ε \varepsilon ε 作 L 2 L_2 L2 损失
Sampling

分布
X
t
X_t
Xt 由高斯分布给出,进行
T
T
T 次循环,从模型
ε
θ
(
X
t
,
t
)
\varepsilon_\theta(X_t,t)
εθ(Xt,t)中获取时刻 t 的高斯分布预测值
ε
θ
\varepsilon_\theta
εθ,通过公式:
X t − 1 = μ ~ t + σ t Z ∼ N ( μ ~ t , σ t ) X_{t-1} = \tilde{\mu}_t + \sigma_tZ \sim \Nu(\tilde{\mu}_t,\sigma_t) Xt−1=μ~t+σtZ∼N(μ~t,σt)
预测前一时刻的分布 X t − 1 X_{t-1} Xt−1,循环该过程得到最终图像 X 0 X_0 X0