1. 语言模型

• 给定文本序列 x1,…,xT,语言模型的目标是估计联合概率p（x1,…,xT）
• 它的应用包括
  • 做预训练模型（eg BERT，GPT-3）
  • 生成文本，给定前面几个词，不断使用xt~p(x1,…,xt-1) 来生成后续文本
  • 判断多个序列中哪个更常见，eg，“to recognize a speech” vs “to wreck a nice beach”

2. 使用计数来建模

3. N元语法

4. 代码实现

4.1 自然语言统计

我们看看在真实数据上如果进行自然语言统计。 根据上一篇文章介绍的时光机器数据集构建词表， 并打印前 10 个最常用的（频率最高的）单词。

import random
import torch
from d2l import torch as d2l

tokens = d2l.tokenize(d2l.read_time_machine())
# 因为每个文本行不一定是一个句子或一个段落，因此我们把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
# for line in tokens： # 获取到每一行
#       for token in line:  # 再获取到每一行的每一个词元token
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]

运行结果：

正如我们所看到的，(最流行的词)看起来很无聊， 这些词通常(被称为停用词)（stop words），因此可以被过滤掉。 尽管如此，它们本身仍然是有意义的，我们仍然会在模型中使用它们。 此外，还有个明显的问题是词频衰减的速度相当地快。 例如，最常用单词的词频对比，第 10 个还不到第 1 个的 1/5 。 为了更好地理解，我们可以画出词频图：

# vocab.token_freqs 一个由多个元组构成的list，每个元组是：（token，出现次数）
freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',
         xscale='log', yscale='log')

运行结果：

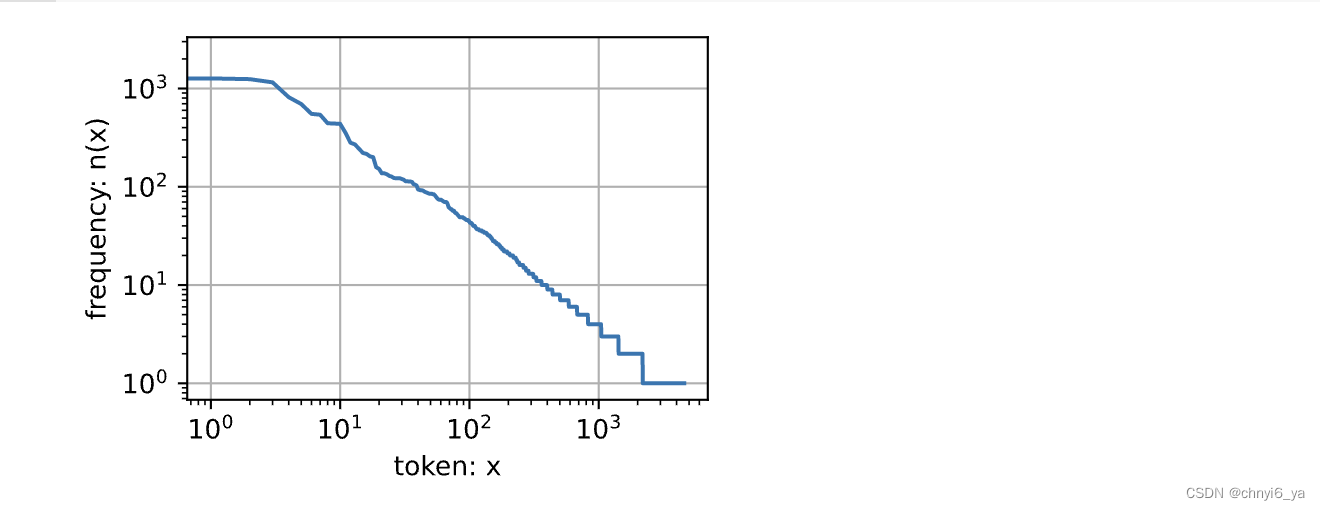
由图可以看出大概两三百个词出现了超过10词，然后后面大概1000个词是没有出现超过10次的。

通过此图我们可以发现：词频以一种明确的方式迅速衰减。 将前几个单词作为例外消除后，剩余的所有单词大致遵循双对数坐标图上的一条直线。 这意味着单词的频率满足齐普夫定律（Zipf’s law）， 即第 𝑖 个最常用单词的频率 𝑛𝑖 为：

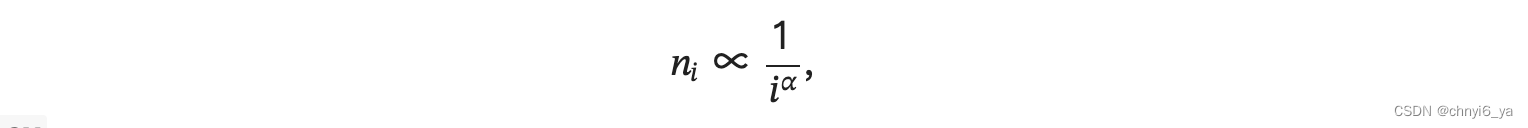
等价于：

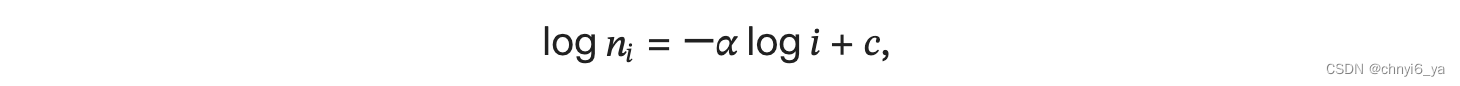
其中 𝛼 是刻画分布的指数， 𝑐 是常数。 这告诉我们想要通过计数统计和平滑来建模单词是不可行的， 因为这样建模的结果会大大高估尾部单词的频率，也就是所谓的不常用单词。 **那么其他的词元组合，比如二元语法、三元语法等等，又会如何呢？**我们来看看二元语法的频率是否与一元语法的频率表现出相同的行为方式。

bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10] # 得到二元词的出现次数

运行结果：

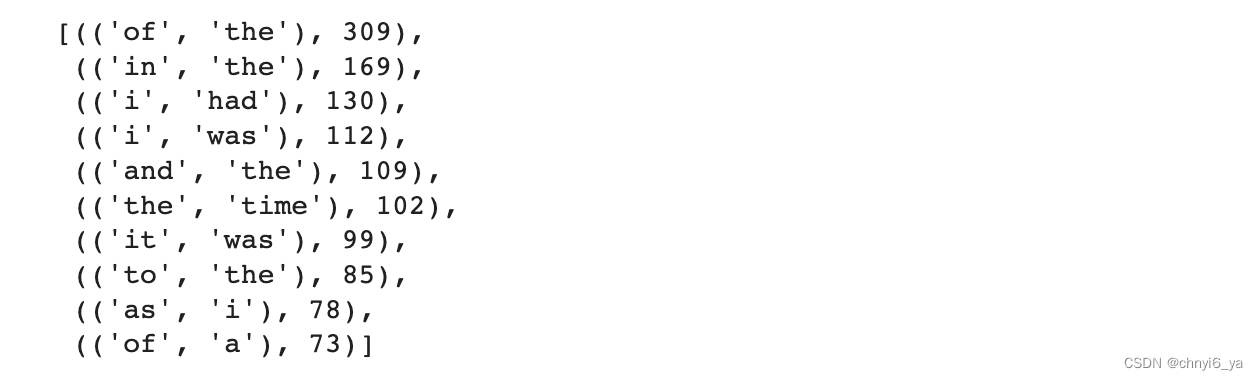
这里值得注意：在十个最频繁的词对中，有九个是由两个停用词组成的， 只有一个与“the time”有关。 我们再进一步看看三元语法的频率是否表现出相同的行为方式。

trigram_tokens = [triple for triple in zip(
    corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10] # 得到三元词的出现次数

运行结果：

最后，我们直观地对比三种模型中的词元频率：一元语法、二元语法和三元语法。

bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
         ylabel='frequency: n(x)', xscale='log', yscale='log',
         legend=['unigram', 'bigram', 'trigram'])

运行结果：

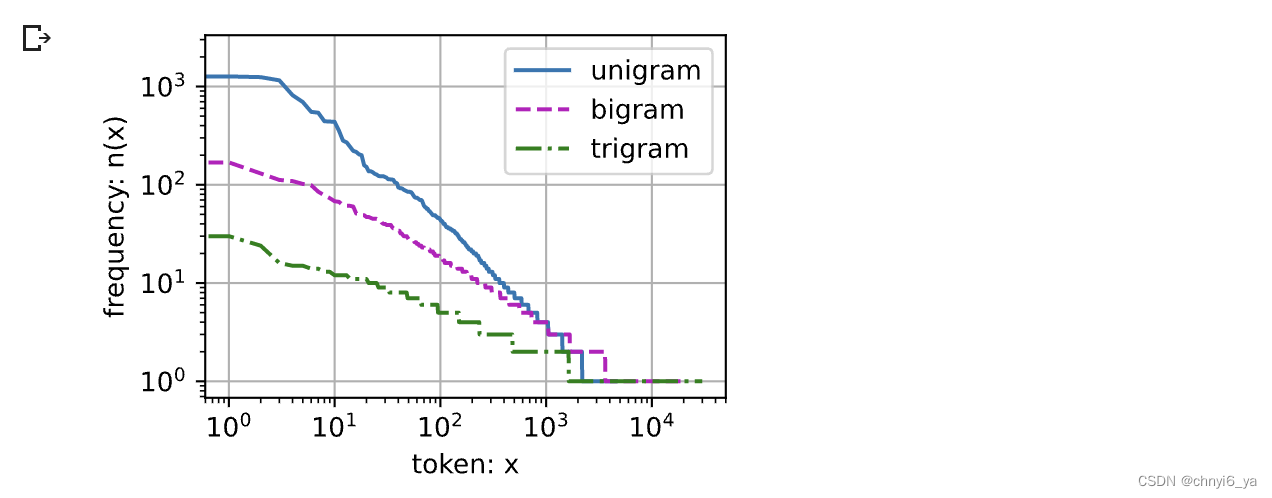
这张图非常令人振奋！原因有很多：

1. 除了一元语法词，单词序列似乎也遵循齐普夫定律， 尽管公式 中的指数 𝛼 更小 （指数的大小受序列长度的影响）；
2. 词表中 𝑛 元组的数量并没有那么大，这说明语言中存在相当多的结构， 这些结构给了我们应用模型的希望；
3. 很多 𝑛 元组很少出现，这使得拉普拉斯平滑非常不适合语言建模。 作为代替，我们将使用基于深度学习的模型。

4.2 读取长序列数据

由于序列数据本质上是连续的，因此我们在处理数据时需要解决这个问题。 我们以一种相当特别的方式做到了这一点： 当序列变得太长而不能被模型一次性全部处理时， 我们可能希望拆分这样的序列方便模型读取。

在介绍该模型之前，我们看一下总体策略。 假设我们将使用神经网络来训练语言模型， 模型中的网络一次处理具有预定义长度 （例如 𝑛 个时间步）的一个小批量序列。 现在的问题是如何随机生成一个小批量数据的特征和标签以供读取。

首先，由于文本序列可以是任意长的， 例如整本《时光机器》（The Time Machine）， 于是任意长的序列可以被我们划分为具有相同时间步数的子序列。 当训练我们的神经网络时，这样的小批量子序列将被输入到模型中。 假设网络一次只处理具有 𝑛 个时间步的子序列。 下图画出了 从原始文本序列获得子序列的所有不同的方式， 其中 𝑛=5 ，并且每个时间步的词元对应于一个字符。 请注意，因为我们可以选择任意偏移量来指示初始位置，所以我们有相当大的自由度。

因此，我们应该选择哪一个呢？ 事实上，他们都一样的好。 然而，如果我们只选择一个偏移量， 那么用于训练网络的、所有可能的子序列的覆盖范围将是有限的。 因此，我们可以从随机偏移量开始划分序列， 以同时获得覆盖性（coverage）和随机性（randomness）。 下面，我们将描述如何实现随机采样（random sampling）和 顺序分区（sequential partitioning）策略。

4.3 随机采样

在随机采样中，每个样本都是在原始的长序列上任意捕获的子序列。在迭代过程中，来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻。 对于语言建模，目标是基于到目前为止我们看到的词元来预测下一个词元， 因此标签是移位了一个词元的原始序列。

下面的代码每次可以从数据中随机生成一个小批量。 在这里，参数batch_size指定了每个小批量中子序列样本的数目， 参数num_steps是每个子序列中预定义的时间步数。

# 可以认为是之前的tau
def seq_data_iter_random(corpus, batch_size, num_steps): 
	# 现在我假设corpus是[0,34]的list，长度为35，batch_size=2，num_steps = 5
    """使用随机抽样生成一个小批量子序列"""
    # 从随机偏移量开始对序列进行分区，随机范围包括num_steps-1
    # random.randint(参数1，参数2)：从[参数1，参数2]中随机取数
    # 从[0,num_steps - 1]中随机取一个数作为序列的起始索引
    # 假设随机从[0,5-1]中抽取的数是1，则corpus是[1,34]
    corpus = corpus[random.randint(0, num_steps - 1):]
    # 减去1，是因为我们需要考虑标签：
    # 如果取到子序列[26,27,28,29,30]那么它的label是[27,28,29,30,31]，
    # 我们需要把最后的“31”保留下来作为label的一部分
    # num_subseqs = 34-1 // 5 = 6...3 也就是说总共有6个子序列，每个子序列长度为5。
    num_subseqs = (len(corpus) - 1) // num_steps
    # 长度为num_steps的子序列的起始索引
    # list(range(1, 30, 5)：[1,6,11,16,21,26]是子序列的起始所索引
    initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
    # 在随机抽样的迭代过程中，
    # 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
    # 把起始索引打乱，如[6，1，11，16，21，26]
    random.shuffle(initial_indices)

    def data(pos):
        # 返回从pos位置开始的长度为num_steps的序列
        # 假设返回[pos:pos+5]的序列
        return corpus[pos: pos + num_steps]

	# 因为假设了batch_size为2，那么num_batches = 6 // 2 =3
	# 也就是说经过3个小批量随机取样，就能遍历一遍完整的所有的子序列
    num_batches = num_subseqs // batch_size
    for i in range(0, batch_size * num_batches, batch_size):
    # range(0, 6, 2)也就是range(0, 2, 4)，因此循环三次即可
        # 在这里，initial_indices包含子序列的随机起始索引
        # [i: i + batch_size]分别是[0,1],[2,3]和[4,5]
        # 去initial_indices中取得到[6,1],[11,16],[21,26]得到initial_indices_per_batch
        # 由此可以看出：到这一步做到了随机抽取,一次抽取2个子序列
        initial_indices_per_batch = initial_indices[i: i + batch_size]
        # [6,1]对应[6,7,8,9,10]和[1,2,3,4,5]
        # [11,16]对应[11,12,13,14,15]和[16,17,18,19,20]
        # [21,26]对应[21,22,23,24,25]和[26,27,28,29,30,31]
        X = [data(j) for j in initial_indices_per_batch]
        # Y与X与之对应的是[7,2],那么子序列分别是[7,8,9,10,11]和[2,3,4,5,6]
        # Y与X与之对应的是[12，17],那么子序列分别是[12,13,14,15,16]和[17，18，19，20，21]
        # Y与X与之对应的是[21，26],那么子序列分别是[21,22,23,24,25]和[26,27,28,29,30,31]
        Y = [data(j + 1) for j in initial_indices_per_batch]
        yield torch.tensor(X), torch.tensor(Y)

总结一下，上面代码的作用就是，传入一个num_steps，选一个随机数，在0到num_steps之间，这之前的token不要了，只对剩余部分做处理，剩余部分平均分成多个长度为num_steps的小句子/子序列，再确定好批量大小，每次迭代就从corpus中随机取一个批量大小的小句子，这样的话，经过一次epoch，也就是扫一次数据，所有的小句子都取到了，只是说可能不同的epoch之间的划分序列是不一样的。

所以有很多epoch时，所有切法都可能被取到，最好的情况就是tau（num_steps）个epoch就能把所有子序列都取到。因为有k（0到tau之间的一个随机值）的存在，使得我们能遍历出所有可能的序列。

ps：以下为简写，以字符为例，可以把每个字符看成一个单词：

下面我们生成一个从 0 到 34 的序列。 假设批量大小为 2 ，时间步数为 5 ，这意味着可以生成 ⌊(35−1)/5⌋=6 个“特征－标签”子序列对。 如果设置小批量大小为 2 ，我们只能得到 3 个小批量。

my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

运行结果：

4.4 顺序分区

在迭代过程中，除了对原始序列可以随机抽样外， 我们还可以保证两个相邻的小批量中的子序列在原始序列上也是相邻的。 这种策略在基于小批量的迭代过程中保留了拆分的子序列的顺序，因此称为顺序分区。

def seq_data_iter_sequential(corpus, batch_size, num_steps):
    """使用顺序分区生成一个小批量子序列"""
    # 从随机偏移量开始划分序列
    offset = random.randint(0, num_steps)
    num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
    Xs = torch.tensor(corpus[offset: offset + num_tokens])
    Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
    Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
    num_batches = Xs.shape[1] // num_steps
    for i in range(0, num_steps * num_batches, num_steps):
        X = Xs[:, i: i + num_steps]
        Y = Ys[:, i: i + num_steps]
        yield X, Y

基于相同的设置，通过顺序分区读取每个小批量的子序列的特征X和标签Y。 通过将它们打印出来可以发现： 迭代期间来自两个相邻的小批量中的子序列在原始序列中确实是相邻的。

for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

运行结果：

现在，我们将上面的两个采样函数包装到一个类中， 以便稍后可以将其用作数据迭代器。

class SeqDataLoader: 
    """加载序列数据的迭代器"""
    def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
        if use_random_iter:
            self.data_iter_fn = d2l.seq_data_iter_random
        else:
            self.data_iter_fn = d2l.seq_data_iter_sequential
        self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
        self.batch_size, self.num_steps = batch_size, num_steps

    def __iter__(self):
        return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)

最后，我们定义了一个函数load_data_time_machine， 它同时返回数据迭代器和词表， 因此可以与其他带有load_data前缀的函数 （如 之前定义的 d2l.load_data_fashion_mnist）类似地使用。

def load_data_time_machine(batch_size, num_steps, 
                           use_random_iter=False, max_tokens=10000):
    """返回时光机器数据集的迭代器和词表"""
    data_iter = SeqDataLoader(
        batch_size, num_steps, use_random_iter, max_tokens)
    return data_iter, data_iter.vocab

总结

• 语言模型估计文本序列的联合概率
• 使用统计方法时，常采用n元语法