一生负气成今日
四海无人对夕阳
目录
树的专辑

树的专辑
1.有n个元素的完全二叉树的深度是( )
A.nlogn
B.nlogn+1
C.logn
D.logn+1
答案:D
解析:
设完全二叉树的节点数为 N,高度为 h ,高度为 h 时空的结点个数为 x
我们根据完全二叉树的性质得:
所以 然后向上取整
2.设一棵二叉树中有3个叶子结点,有8个度为1的结点,则该二叉树中总的结点数为( )个
A.11
B.12
C.13
D.14
答案:C
解析:
设 Ni 表示度为 i 的节点个数,则节点总数 N = N0 + N1 + N2
节点个数于节点边的关系:
N 个节点的树有 N-1 个边
边与度的关系:N - 1 = N1 + 2 * N2
故:N0 + N1 + N2 - 1 = N1 + 2 * N2
因此,得:N0 = N2 + 1
回到原题,N0 = 3,N1 = 8,可得N2 = 2
因此答案是 3 + 8 + 2 = 13
3.一颗完全二叉树有1001个结点,其叶子结点的个数是( )
A.251
B.500
C.501
D.不能确定
答案:C
解析:
首先我们知道任意一棵二叉树都有 N0 = N2 + 1 性质(设 Ni 表示度为 i 的节点个数)
另外,在完全二叉树中,如果节点总个数为奇数,则没有度为 1 的节点,如果节点总个数为偶数,只有一个度为 1 的节点
我们分类讨论即可:
当节点数为偶数时,N = N2 + N0 + 1 即 N = 2N0 (因为算出是分数,所以不合理,即没有度为1的节点)
当节点数为奇数时,N = N2 + N0 即 N = 2N0 - 1 (解出的结果得:N0 = 501)
4.在一颗度为3的树中,度为3的结点有2个,度为2的结点有1个,度为1的结点有2个,则叶子结点有( )个
A.4
B.5
C.6
D.7
答案:C
解析:
设度为 i 的节点个数为 Ni,该树总共有 N 个节点,则 N = N0 + N1 + N2 + N3
根据我们之前所学的知识:我们知道:一颗 N 节点的数有N-1条边 (该树中除了根节点没有前驱以外,每个节点有且只有一个前驱)
根据度的定义,总边数与度之间的关系为:N-1 = 0*N0 + 1*N1 + 2*N2 + 3*N3
带入节点联立 N = N0 + N1 + N2 + N3 和 N-1 = 0*N0 + 1*N1 + 2*N2 + 3*N3 两个方程
解得:N0 = 6
5.一颗拥有1000个结点的树度为4,则它的最小深度是( )
A.5
B.6
C.7
D.8
答案:B
解析:
如果这棵树每一层都是满的,则它的深度最小,假设它为一个四叉树,高度为h,则这个数的节点个数为
节点数: 1 + 4*4^0 + 4*4^1 + 4*4^h-1 1 2 3 h 层 层 层 层 整棵树的节点得:4^0+4^1+4^2+...+4^(h-1) 等比数列求和=(4^h-1)/3
当 h = 5,最大节点数为 341, 当 h = 6,最大节点数为 1365,所以最小深度应该为 6
6.已知某二叉树的前序遍历序列为5 7 4 9 6 2 1,中序遍历序列为4 7 5 6 9 1 2,则其后序遍历序列为( )
A.4 2 5 7 6 9 1
B.4 2 7 5 6 9 1
C.4 7 6 1 2 9 5
D.4 7 2 9 5 6 1
答案:C
解析:
我们可以通过:前序遍历找到子树的根,在中序遍历中找到根的位置,然后确定根左右子树的区间
首先我们根据前序找到根节点:
5 7 4 9 6 2 1
然后在中序中找到根节点的位置:
4 7 5 6 9 1 2
这个时候 4 7 就是 5 的左子树,6 9 6 2 1 就是 5 的右子树

然后我们可以根据这个规律将这颗树补全:
我们再回到前序:7 4 9 6 2 1
这个时候 7 就是5的左子树即当前的根
再回到中序:4 7 6 9 1 2
这个时候 4 就是 7 的左子树
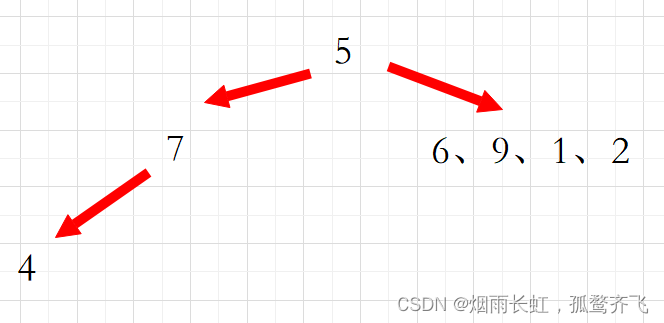
再回到前序: 9 6 2 1
这个时候 开始构建右子树,而 9 就是 5 的右子树即当前根
再回到中序: 6 9 1 2
这个时候 6 就是 9 的左子树,1 2 在 9 的右子树上
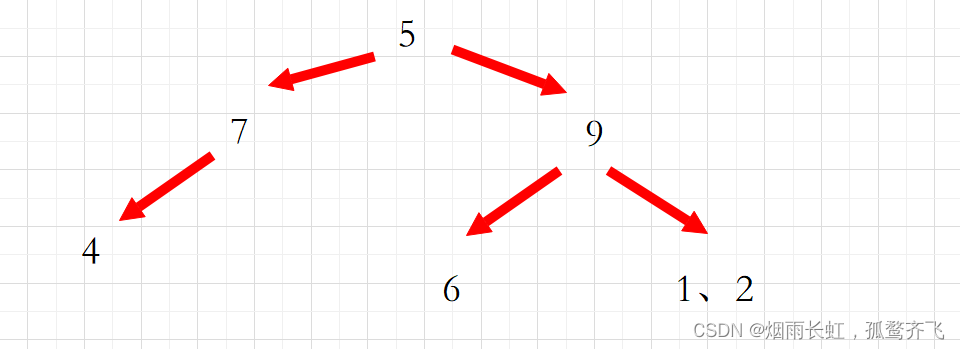
再回到前序: 2 1
这个时候 2 就是 9 的右子树即当前根
再回到中序: 1 2
这个时候 1 就是 2 的左子树,这个时候树已经构建完成了
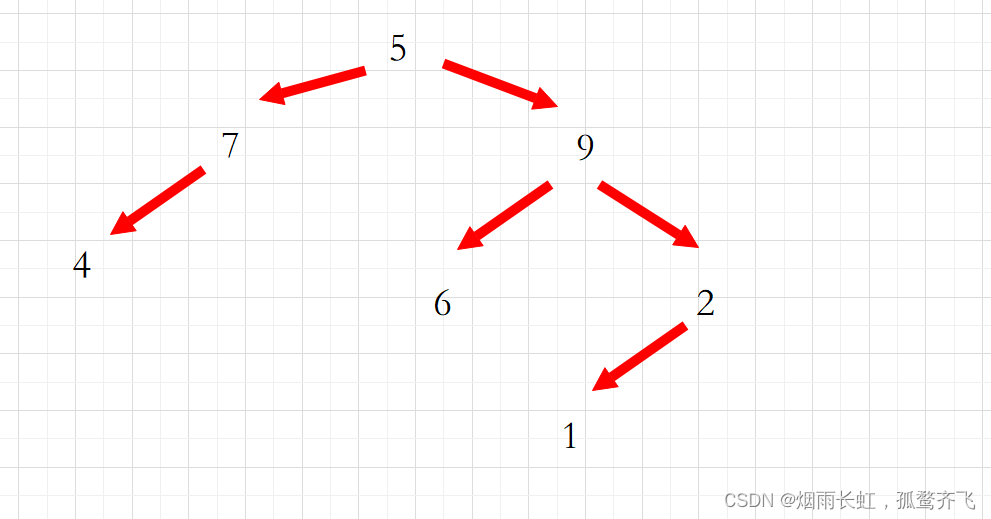
我们再根据后序遍历的规律就可以得出答案了 ! ! !
7.如果一颗二叉树的前序遍历的结果是ABCD,则满足条件的不同的二叉树有( )种
A.13
B.14
C.15
D.16
答案:B
解析:
首先这棵二叉树的高度一定在3~4层之间:
三层:
A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),
A(B,C(D,())), A(B,C((),D))一共 6 种
四层:
如果为四层,就是单边树,每一层只有一个节点,除过根节点A,其他节点都有两种选择,在上层节点的左边还是右边,所以2*2*2共8种
总共为 14 种
8.设根结点的深度为1,则一个拥有n个结点的二叉树的深度一定在( )区间内
A.[log(n + 1),n]
B.[logn,n]
C.[log(n + 1),n - 1]
D.[log(n + 1),n + 1]
答案:C
解析:
首先我们知道拥有n个结点的二叉树的:
最大深度的模型就是单边数,节点数即深度,也就是 n
最小深度的模型可以看作完全二叉树,根据性质: h = log(n+1) 向上取整
也就是说:二叉树的深度范围在 [log(n + 1),n] 之间
9.设某种二叉树有如下特点:每个结点要么是叶子结点,要么有2棵子树。假如一棵这样的二叉树中有m(m>0)个叶子结点,那么该二叉树上的结点总数为( )
A.2m+1
B.2(m-1)
C.2m-1
D.2m
答案:C
解析:
根据二叉树的性质,在任意的二叉树中,度为 0 的节点比度为 2 的节点多了 1 个
现在叶子节点为 m 个,即度为 0 的节点有 m 个,那度为 2 的节点个数就为 m-1 个
而题目说该二叉树中只有度为2和度为0的节点 ,因此总的节点数就为:N = m+m-1 = 2m-1
10.一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足( )
A.所有的结点均无左孩子
B.所有的结点均无右孩子
C.只有一个叶子结点
D.至多只有一个结点
答案:C
解析:
前序遍历:根 左 右
后序遍历:左 右 根
从二叉树 前序 和 后序遍历结果规则中可以看出,如果树中每个节点只有一个孩子时,遍历结果肯定是反的
比如下面这前序和中序序列所构成的树的结构:
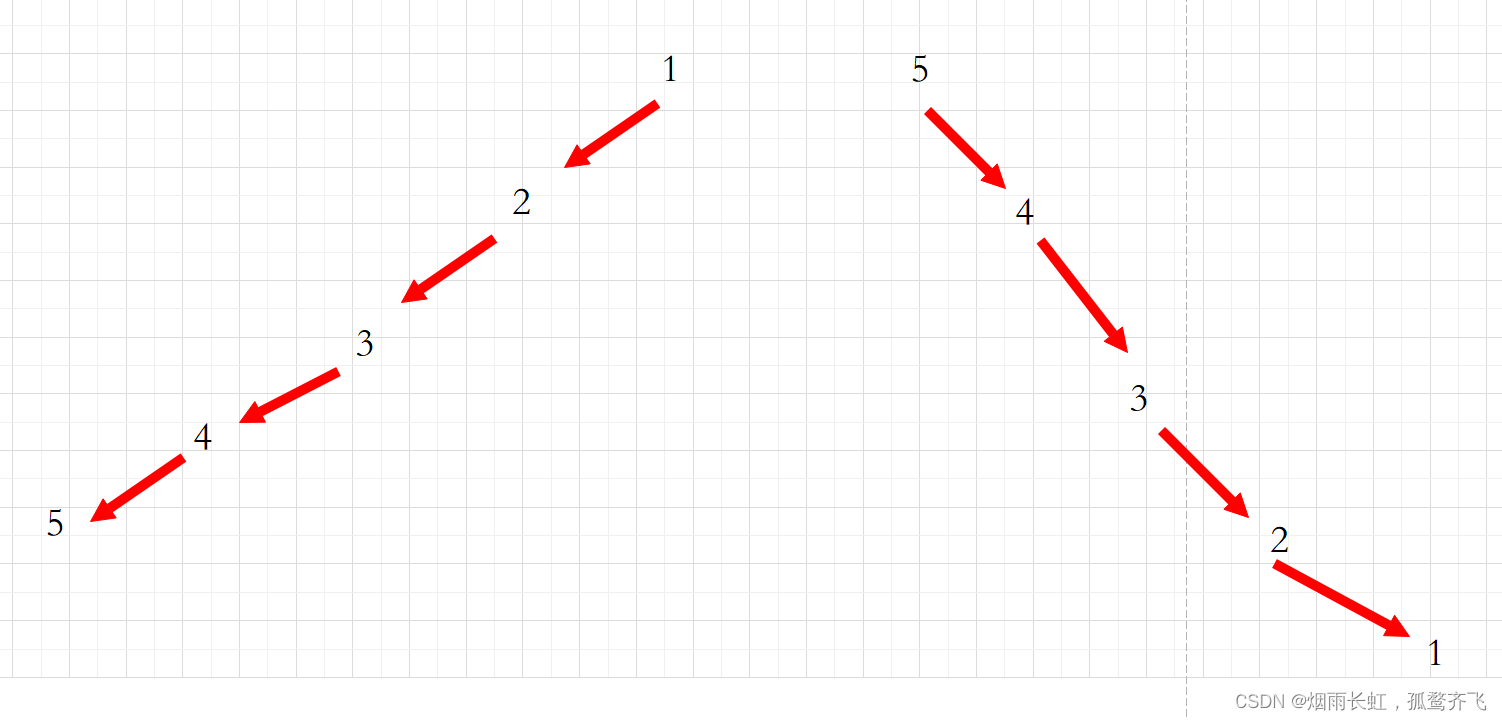
故每个节点只有一个孩子,即只有一个叶子节点
11.设哈夫曼树中有199个结点,则该哈夫曼树中有( )个叶子结点。
A.100
B.99
C.101
D.102
答案:A
解析:
根据哈夫曼树的性质:两两节点相结合形成的树,所以没有度为 1 的节点
再根据二叉树的特性:度为 0 的节点比度为 2 的节点多了 1 个(即:N0 = N2 + 1)
所以 N = N0 + N2 和 N0 = N2 + 1 联立解得:N0 = 100
12.将一株有100个节点的完全二叉树从上到下,从左到右依次进行编号,根节点的编号为1,则编号为49的节点的 左孩子编号为( )
A.89
B.98
C.50
D.25
答案:B
解析:

设父节点为parent,孩子节点为child,当前编号 n,我们根据二叉树的性质得:
对于偶数节点(左孩子)其父节点:parent = n / 2
对于奇数节点(右孩子)其父节点:parent = (n-1) / 2
98 为偶数,其父节点编号为 98 / 2 = 49
13.由权值分别为 9、2、5、7、4 的5个叶子结点构造一棵哈夫曼树,则该树的带权路径长度为( )
A.65
B.45
C.55D.60
答案:D
解析:
首先我们需要构建一颗哈夫曼树:
构建方法:
对于给定的有各自权值的 n 个结点
<1>在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和 <2>在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推 <3>重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树
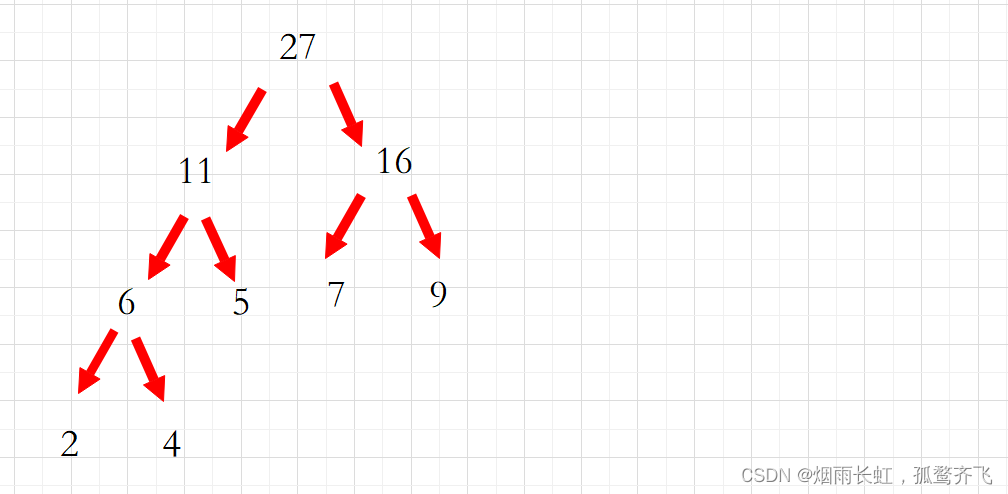
带权路径长度是指所有叶子结点深度乘以其权值之和,也就是:(2+4)*3 + (5+7+9)*2 = 60