在日常商旅过程中，出差行程计划是必不可少的环节。公司需要以此为依据判断行程是否有必要、是否合理，确保出差行程与公司的业务需求相符。

　　通过胜意费控云，员工填写出差申请时，行程计划智能生成，平台自动匹配并带出差标，员工心中有底，出差更安心；同时还支持实时行程查询，带入精确预算数据，领导审批更直观、更简单、更有依据，财务报销审核更高效、费控更合规！

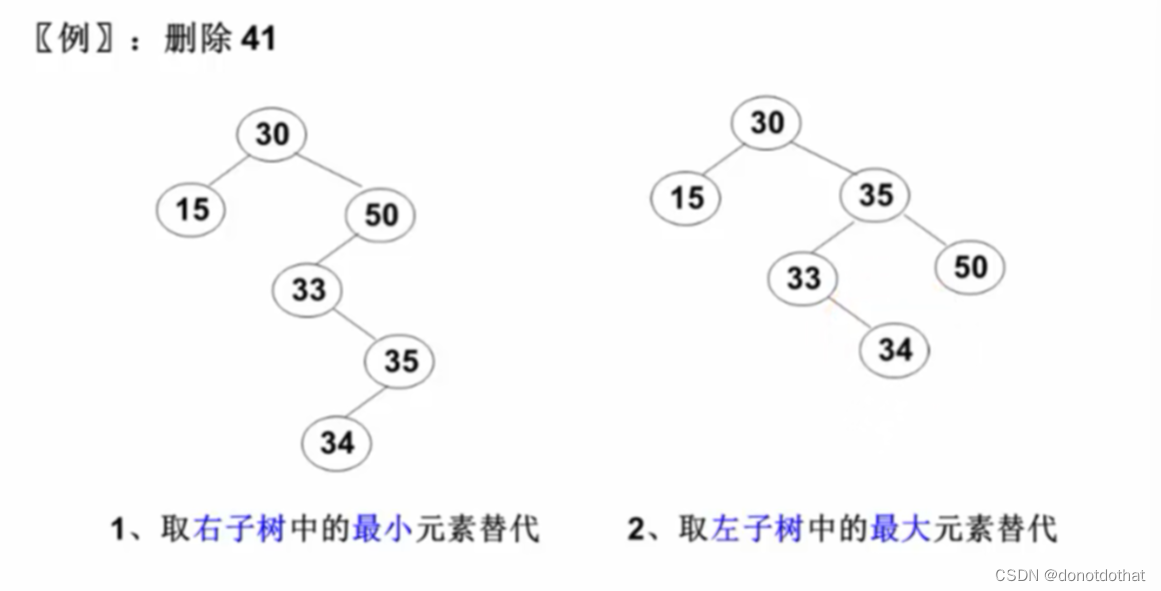
　　一、行程具体安排自动带入，出差行程规划更高效

　　员工填写出差申请时，平台自动根据填写的出差类型、出差日期、出发地、目的地等基本信息，同步生成行程计划。

　　行程按照去程、回程分别列出，按机票、火车票、酒店等分别规划，员工可根据实际交通、住宿安排对出行计划进行调整，无需手动查询、填写，出差计划制定更高效。

　　二、差标自动匹配，预订不怕超标

　　预订时为了不超标要小心再小心？通过胜意费控云，员工填写行程计划时，自动获取差标并带出，可点击“明细”，查看详细情况，费用标准一目了然。

　　预订机票、酒店、火车、用车时，系统自动进行差旅标准控制，例如[允许乘坐舱位：普通经济舱]、[不得高于7折]，在差旅标准内的允许预订，不在标准内的显示[超]，提示不允许预订，也可设置不显示，堵住预订的超标“黑洞”。

　　还可设置超标个人支付，或二次审批，企业可根据自身管控需求进行自定义，保障消费合规的同时，又可有效管控成本。

　　三、行程实时查询，费用评估更有依据

　　胜意费控云支持通过[实时查询]精确带入行程预算。查询时，自动带入出行时间、人员等相关信息，实时筛选出符合条件的订单，员工点击“预订”自动回填至“费用预算”一栏，精准预测费用，领导审批后方可预订。

　　提交送审后，管理者可查看相关行程明细，可以提前掌握员工的差旅计划和相关明细，知悉员工业务拓展情况，并根据业务部门规划进行调整绩效或预算。

　　四、平台数据联动，助力财务审核提效

　　对于部门较多，业务结构较复杂的企业在进行审计的时候就会发现，费用报销是舞弊的重灾区之一。财务往往要花费诸多时间精力审核员工报销的真实性、合理性和合规性。

　　使用胜意费控云后，员工提交差旅申请单，填写行程明细，自动关联预算和差标进行管控，业务审批通过后方可预订，审核时可直接调取出行状态，平台管控环环相扣，全流程数据打通，无需人工判断费用是否真实、合理、合规。根据业务类型预先设置好校验规则后，智能审单机器人即可自动完成费用报销审核，财务工作省心又高效。