#需要资源(软件包及镜像)或有问题的,可私聊博主!!!
#需要资源(软件包及镜像)或有问题的,可私聊博主!!!
#需要资源(软件包及镜像)或有问题的,可私聊博主!!!
某企业根据自身业务需求,实施数字化转型,规划和建设数字化平台,平台聚焦“DevOps开发运维一体化”和“数据驱动产品开发”,拟采用开源OpenStack搭建企业内部私有云平台,开源Kubernetes搭建云原生服务平台,选择国内主流公有云平台服务,基于数字化平台底座,面向业务开发边缘计算云应用产品。
拟将该任务交给工程师A与B,分工协助完成云平台服务部署、云应用开发、云系统运维等任务,系统架构如图1所示,IP地址规划如表1所示。
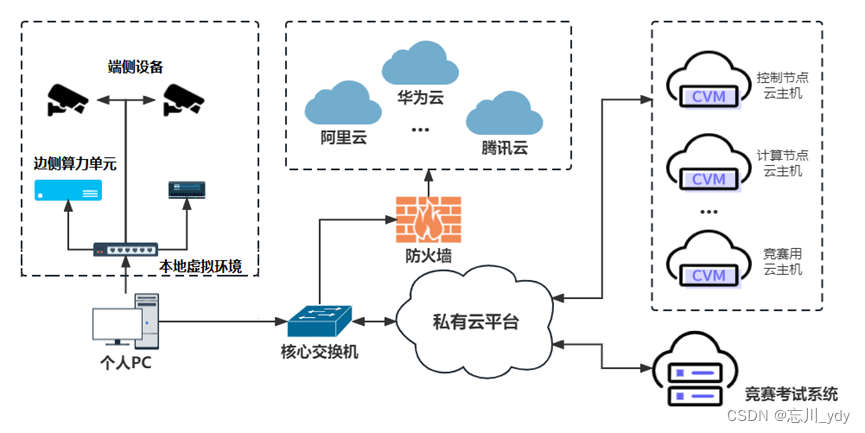
图 1 系统架构图
表 1 IP 地址规划
| 设备名称 | 主机名 | 接 口 | IP 地址 | 说明 |
| 云服务器 1 | controller | eth0 | 172.129.x.0/24 | vlan x |
| eth1 | 自定义 | 自行创建 | ||
| 云服务器 2 | compute | eth0 | 172.129.x.0/24 | vlan x |
| eth1 | 自定义 | 自行创建 | ||
| 云服务器 3 ... 云服务器n | 自定义 | eth0 | 172.129.x.0/24 | |
| PC-1 | 本地连接 | 172.24.16.0/24 | PC 使用 |
说明
1.竞赛使用集群模式进行,比赛时给每个参赛队提供独立的租户与用户,各用户的资源配额相同,参赛选手通过用户名与密码登录竞赛用私有云平台,创建云主机进行相应答题,2名参赛选手的账号密码相同;
2.表中的x为赛位号,在进行OpenStack搭建时的第二块网卡地址根据题意自行创建;
3.根据图表给出的信息,检查硬件连线及网络设备配置,确保网络连接正常;
4.考试所需要的账号资源、竞赛资源包与附件均会在考位信息表与设备确认单中给出;
5.竞赛过程中,为确保服务器的安全,请自行修改服务器密码;在考试系统提交信息时,请确认自己的IP地址,用户名和密码。
模块一 私有云(30分)
企业首先完成私有云平台搭建和运维,私有云平台提供云主机、云网络、云存储等基础架构云服务,并开发自动化运维程序。
任务1 私有云服务搭建(5分)
1.1.1 基础环境配置
1.控制节点主机名为controller,设置计算节点主机名为compute;
2.hosts文件将IP地址映射为主机名。
1.1.2 yum源配置
使用提供的http服务地址,分别设置controller节点和compute节点的yum源文件http.repo。
1.1.3 配置无秘钥ssh
配置controller节点可以无秘钥访问compute节点。
1.1.4 基础安装
在控制节点和计算节点上分别安装openstack-iaas软件包。
1.1.5 数据库安装与调优
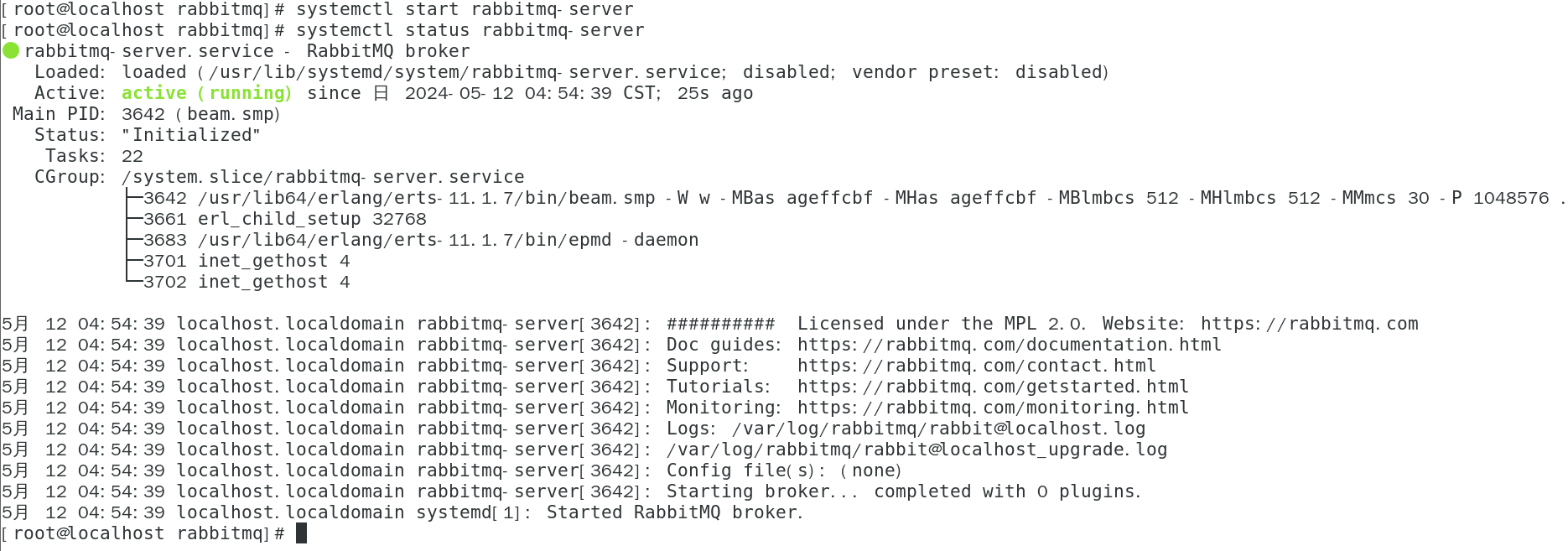
在控制节点上使用安装Mariadb、RabbitMQ等服务。并进行相关操作。
1.1.6 Keystone服务安装与使用
在控制节点上安装Keystone服务并创建用户。
1.1.7 Glance安装与使用
在控制节点上安装Glance 服务。上传镜像至平台,并设置镜像启动的要求参数。
1.1.8 Nova安装
在控制节点和计算节点上分别安装Nova服务。安装完成后,完成Nova相关配置。
1.1.9 Neutron安装
在控制和计算节点上正确安装Neutron服务。
1.1.10 Dashboard安装
在控制节点上安装Dashboard服务。安装完成后,将Dashboard中的 Django数据修改为存储在文件中。
1.1.11 Swift安装
在控制节点和计算节点上分别安装Swift服务。安装完成后,将cirros镜像进行分片存储。
1.1.12 Cinder创建硬盘
在控制节点和计算节点分别安装Cinder服务,请在计算节点,对块存储进行扩容操作。
1.1.13 Barbican服务安装与使用
在控制节点安装barbican服务,安装服务完毕后,创建一个密钥。
任务2 私有云服务运维(15分)
1.2.1 Glance镜像上传
在OpenStack私有云平台上,使用cirros-0.3.4-x86_64-disk.img镜像创建一个名为cirros的镜像。
1.2.2 RPM包管理
解决依赖包冲突,安装libguestfs-tools工具。
1.2.3 Raid磁盘阵列管理
在云主机上对云硬盘进行操作,先进行分区,然后创建名为/dev/md5、raid级别为5的磁盘阵列加一个热备盘。
1.2.4 使用Heat模板创建flavor
编写模板server.yaml,按要求创建云主机类型。
1.2.5 虚拟机调整flavor
使用OpenStack私有云平台,请修改相应配置,实现云主机调整实例大小可以使用。
1.2.6 快照管理
在OpenStack私有云平台上,创建云主机VM1并打快照,使用qemu-img相关命令,修改compat版本。
1.2.7 Swift配置Glance后端存储
使用OpenStack私有云平台,修改相应的配置文件,使对象存储Swift作为glance镜像服务的后端存储。
1.2.8 Glance镜像存储限制
在OpenStack平台上,请修改Glance后端配置文件,将用户的镜像存储配额限制为20GB。
1.2.9 RabbitMQ集群部署
使用OpenStack私有云平台,创建三个云主机搭建RabbitMQ集群。
1.2.10 云平台安全策略提升
使用OpenStack,安装必要组件,将私有云平台的访问策略从http提升至https。
1.2.11 完成私有云平台的调优或排错工作。(本任务只公布考试范围,不公布赛题)
任务3 私有云运维开发(10分)
1.3.1 编写Shell脚本备份数据库
编写数据库的定期备份shell脚本。
1.3.2 Ansible部署MariaDB服务
编写Ansible脚本,部署MariaDB服务。
1.3.3 Ansible部署ELK服务
编写Playbook,部署的ELK。
1.3.4 编写OpenStack容器云平台自动化运维工具。(本任务只公布考试范围,不公布赛题)
![[数据集][目标检测]管道焊缝质量检测数据集VOC+YOLO格式1134张2类别](https://img-blog.csdnimg.cn/direct/081289cc7bd648c4a095943bfdbf78f6.png)