1、二叉树的遍历

1.1先序、中序、后序遍历

先序遍历

根->左->右

先序遍历先访问根节点，再访问它的左子树，然后访问它的右子树。对于每次访问到的结点，都要递归地访问左子树、后右子树———递归。
创建

typedef struct TreeNode* BinTree;
struct TreeNode {
	int Data;
	BinTree Left;
	BinTree Right;
};
void PreOrderTraversal(BinTree BT)
{//先看树空不空，如果是空的退出函数
	if(BT)
	{
		printf("%d",BT->Data);//先根节点
		PreOrderTraversal(BT->Left);//再左子树
		PreOrderTraversal(BT->Right);//后右子树
	}
}

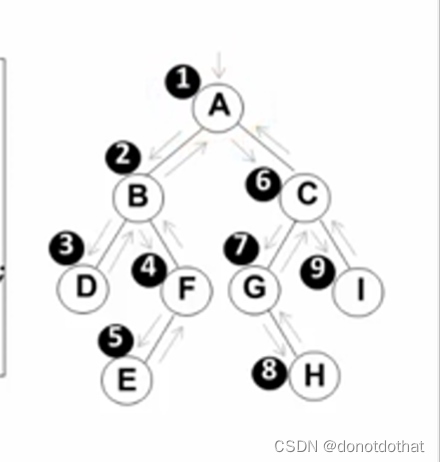
遍历的顺序就是ABDFECGHI

中序遍历

左->根->右

void InOrderTraversal(BinTree BT)
{
	if( BT )
	{
		InOrderTraversal(BT->Left);//先左子树
		printf("%d",BT->Data);//再根节点
		InOrderTraversal(BT->Right);//后右子树
	}
}

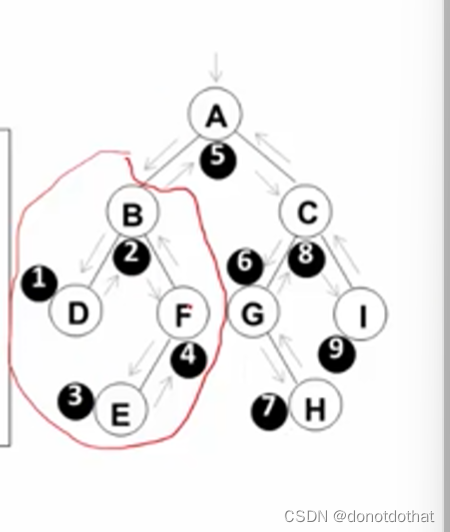
先将左半B部分打印出来，再打印A，再打印右半C部分。在B部分这边，先打印D部分，再打印F部分。在D部分这边…依次先对左递归，再中，再右边。

后序遍历

左->右->根

void InOrderTraversal(BinTree BT)
{
	if( BT )
	{
		InOrderTraversal(BT->Left);//先左子树
		InOrderTraversal(BT->Right);//再右子树
		printf("%d",BT->Data);//再根节点
	}
}

每到一个新的节点，都是先左：先左下去；再回来：再右；

三个遍历都是先左后右，先序（根左右）、中序（左根右）、后序（左右根）说的是根的位置；->先序遍历根节点在第一个；后序遍历根节点在最后一个。

中序遍历非递归遍历算法

按照一个整体的路线进行堆栈的操作。按照左->中->右的顺序，碰到一个节点就放入堆栈，向左边走，左边走到底，返回的时候就抛出结点；然后往右边走…

void InOrderTraversal( BinTree BT )
{
	BinTree T = BT;
	Stack S = CreatStrack( Maxsize );//创建一个堆栈
	while(T || !IsEmpty(S) )//当其中之一不空的时候（循环到树T和堆栈S全都为空为止）
	{
		while(T)//当T存在，循环到T为NULL
		{
			Push(T);//先将非空的T压入栈
			T = T->Left;//继续向左边走
		}
		if( !IsEmpty(S) )//如果堆栈还存在节点
		{	
			T = Pop(S); printf("%d",T->Data);//弹出堆栈并访问打印
			T = T->Right;//第一次内循环结束，以右子树为新起点开启新一轮循环。判断外循环条件。
		}
	}
}

第一次碰到的时候push进去，第二次碰到的时候Pop出去。

1.2层序遍历

二叉树遍历的核心就是把二维的结构线性化，变成一个一维的线性序列的过程。在访问过程中，都是从一个节点开始访问，通过这个节点访问他的左右儿子。访问它的左儿子的时候，通过这个左儿子又开始访问子节点…由于访问节点只能通过父节点来访问，从这个结点访问到了左节点，那么右儿子怎么办？那么就需要保存这个父节点（或者保存右儿子），就能够再访问右儿子。

队列实现

先让根节点入队，开始循环操作：根节点出队，把他的左右儿子入队；继续出队队列中的下一个节点，把他的左右儿子入队；继续出队下一个节点，把他的左右儿子入队…这样就会完成遍历。
特征：一层一层遍历，循环“出队，入队他的左右节点”

void LevelOrderTraversal( BinTree BT )
{
	Queue Q;//队列
	BinTree T;//树
	if( !BT ) return;
	else
	{
		Q = CreatQueue(MaxSize);
		AddQ(Q,BT);//将根节点入队，开始循环的时候一定是不空的
		while( !IsEmptyQ( Q ) )//
		{//循环做三件事情：一个出队，并将他的左右节点入队
			T = DeleteQ(Q);//出队一个节点，返回给T
			printf("%d",T->Data);//访问
			//添加它的左右节点：（注意判断是否存在）
			if(T->Left) AddQ(Q,T->Left);
			if(T->Right) AddQ(Q,T->Right);
			
		}
	}
}

1.3遍历的应用例子

输出二叉树中的叶子结点

基于前序遍历输出：

void PreOrderTraversal( BinTree BT)
{
	if( BT )
	{//基于前序遍历，只是增加一个判断条件
		if( !BT->Left && !BT->Right )
		{
			print("%d",BT->Data);
		}
		PreOrderTraversal( BT->Left);
		PreOrderTraversal( BT->Right);
	}
}

求二叉树的高度

树是递归定义的，以递归来实现：一个树的高度 = 左右子树最大高度 + 1 ，所以必须知道左右两个子树的高度，才能求出它的高度。
所以基于后序遍历来实现

int PostOrderGetHeight( BinTree BT )
{
	if( !BT ) return 0 ;//不存在的情况
	else 
	{
		HL = PostOrderGetHeight(BT->Right);//递归左子树的深度；
		HR = PostOrderGetHeight(BT->Right);//递归右子树的深度；
		MaxH = (HL > HR)? HL : HR ;//条件表达式找出最大深度
		return (MaxH + 1);
	}
}

二元运算表达式树 及其遍历

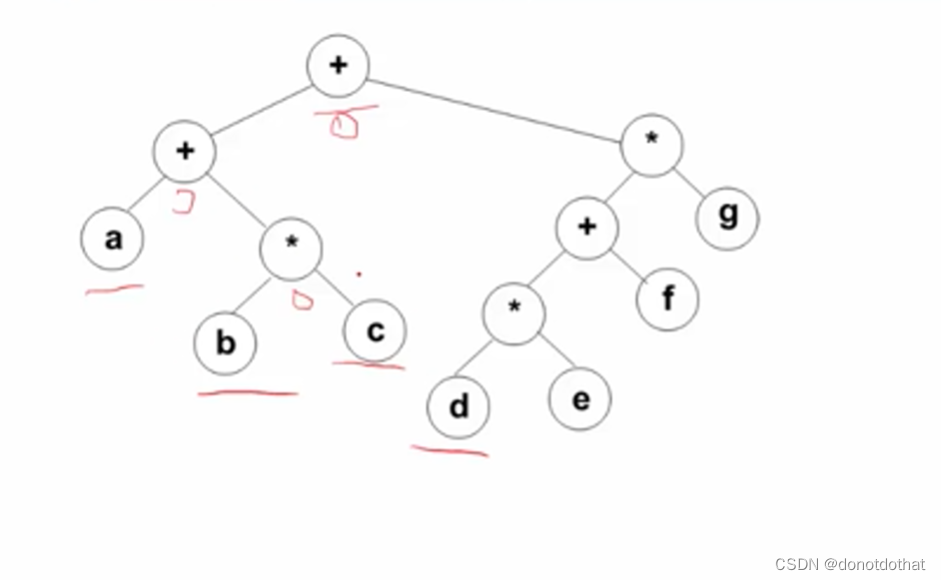
叶节点都是运算数，非叶结点都是都是运算符号。
三种遍历方式可以得到三种不同的表达式：

其中，中缀表达式会受到运算符优先级的影响（不准确）。

由两种遍历序列确定二叉树

根是容易确定的，先序遍历的第一个结点就是根；后序遍历的最后一个节点就是根。只能由先序/后序 + 中序才能唯一的确定一个二叉树。
------->先序+中序：

• 先由先序序列第一个节点确定根节点；
• 在中序序列找到根节点，那么这个根节点就将中序序列分割成先序遍历的左子树和先序遍历的右子树；
• 在先序序列的根节点向后找到先序遍历的左子树和先序序列的右子树；
• 那么就分别得到了先序序列和中序序列的左右子树，重复操作。
  

2.二叉树的同构

表示方式：
使用结构数组的方式每个数组单元包括char类型的节点名称、左子树对应的下标、右子树对应的下标。下标从0开始。

3.二叉搜索树

对于任何节点，其左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。
保持二叉搜索树的前提是保证它的有序性。

3.1查找功能

静态查找：查找的元素是不动的，在一个集合上主要是Find操作，没有插入与删除。二分查找是一个很好的方法；
动态查找：除了Find，还有插入与删除的操作；
二叉搜索树：左子树 < 根节点 < 右子树
主要的功能函数：

查找特定值

BnTree Find(int x,BinTree BST)
 {
 	if(BST == NULL) return NULL;//二叉树为空，直接返回
 	if(x < BST->Data)
 	{
 		return Find(x,BST->Left);//注意要有返回值，一定要是return,在左子树中继续查找
 	}
 	else if(x > BST->Data)
 	{
 		return Find(x,BST->Right);//再右子树中继续查找
 	}
 	else return BST;//剩下的情况就是x == BTS->Data
 }

以上代码是通过尾递归（在程序return时递归）的方式实现的，效率不是很高；可以将尾递归函数改为迭代函数，即尾递归可以用循环来实现：

BinTree Find(int x,BinTree BST)
{
	if(BST == NULL)  return NULL;//空二叉树
	BinTree Temp = BST;
	while(Temp)
	{//当Temp存在的时候执行：
		if(x > Temp->Data) Temp = Temp->Right;
		else if(x < Temp->Data) Temp = Temp->Left;
		else return Temp; //x == Temp的情况
	}
	return NULL;//找不到，二叉树中不存在x
}

查找的效率取决于树的高度

最大查找和最小查找

由于二叉树从根节点开始，向左Data值一直减小，向右Data值一直增大，故可以得出最小Data值在最深层的左子树节点，最大Data值在最深层的右子树节点。
可以确定的是，最大/最小结点一定不是具有两个儿子的节点。

既可以通过递归实现，也可以通过循环实现

• 循环算法：

BinTree FindMin(BinTree BST)
{
	BinTree Temp = BST;
	if(Temp)//这个if语句主要是针对Temp是否存在
	{
		while(Temp->Left)
		{//当左子树存在的时候，一直向左边走
			Temp = Temp->Left; 
		}
	}
	return Temp;//这里对BST为空的时候也适用
}

• 递归算法：

BinTree Temp = BTS;
BinTree FindMax(Temp)
{
	if( Temp == NULL) return NULL;//这个主要用于首次判断
	//递归部分：
	else if(Temp->Right)
	{
		return FindMax(Temp->Right);//大都返回函数
	}//当递归到了Temp没有右子树的时候，此时的Temp就是所找的最深的右子树
	else return Temp;//最后返回指针，回溯
}

二叉搜索树的插入*

在理解递归的时候，形式参数BTS、函数体内部的BTS就可以理解为在递归过程中具体的树节点

BinTree Insert(int x,BinTree BST)//函数通过返回节点来实现赋值（插入）操作
{
	if( !BST )//递归到参数结点为空的时候
	{
		//因为是空的，所以申请空间完成赋值
		BinTree BST = malloc(sizeof(struct TreeNode));
		BST->Data = x;
		BST->Left = BST->Right = NULL;
	}
	else if(x < BST->Data)//x小于此节点，向左	
	{
		BST->Left = Insert(x,BST->Left);
	}
	else if(x > BST->Data)//继续向右
	{
		BST->Right = Insert(x,BST->Right);
	}
	/*else  x = BST->Data,表示X已经存在，不用操作*/
	return BST;//这里BST是抽象的形式参数，返回的指针取决于传入的BST具体是什么
}

函数的出口只有一个return BST;，无论是创造一个新节点还是BST->Right = Insert(x,33->Right);每次Insert函数最后都会返回某个具体的节点；
eg,当递归到了叶节点33，还差一步即将完成插入35操作。叶节点33存在，首先33号->Data < 35，那么就将35继续向右走下去，执行33->Right = Insert(x,33->Right);因为33->RIght == NULL，所以就意味着要为33号结点创建一个右节点并且将35储存到这里，Insert()函数执行完毕之后就创建了一个新节点，并且把储存了35的右节点返回给33->Right，这就完成了插入操作。之后就层层递归返回，直至真正的BST返回到首次Insert函数，完成整个递归过程。

• 当Insert函数的BST参数为NULL时，意味着已经到达了应该插入新节点的位置。
• 整个过程是递归的，每一步都是重复决策的过程：比较当前节点的值，并根据比较结果向左或向右移动，直到找到一个空位置来插入新节点。
• 其中的有效赋值只是将x进行赋值，其他赋值都是重复赋值，例如BST->Right = BST->Right(函数的返回值）;
• return BST;这里BST是抽象的形式参数，形式参数是啥最后就会返回啥，如果一个节点不空，当递归回溯的时候，这一步还是返回此节点指针。

二叉搜索树的删除

要实现删除操作，需要先找到目标节点（要删除的节点），然后执行操作。
目标结点分为几种：

1. 叶节点：直接删除就好
2. 只有左儿子/右儿子的结点：把已删除结点的儿子连接到上一层
3. 既有左儿子也有右儿子的节点：
   

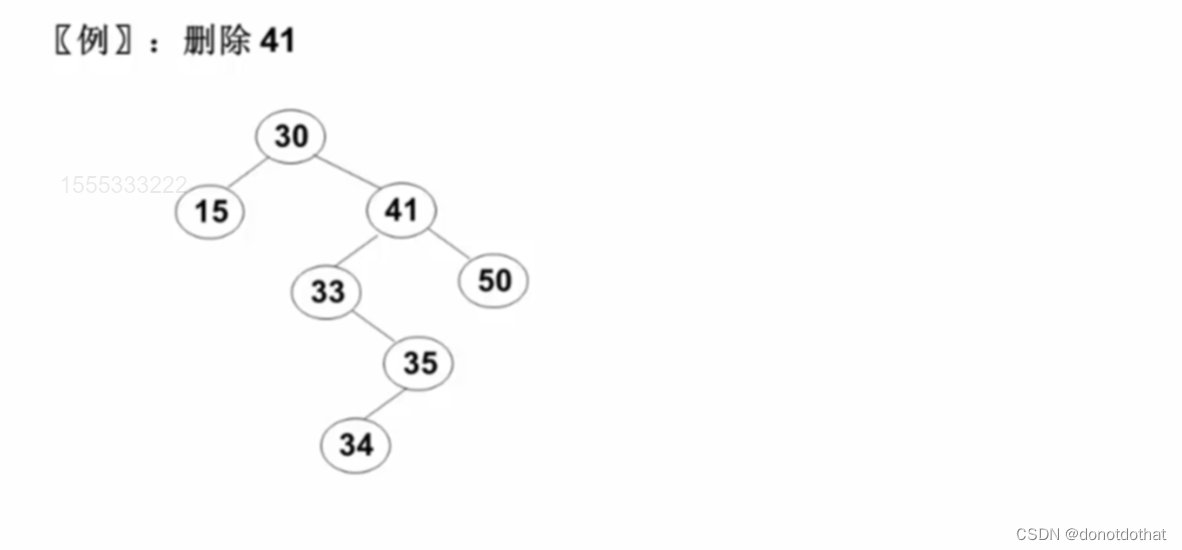
这种情况有些复杂，需要转化问题。有两种思路：一种是将目标节点用右子树的最小节点替代；另一种方法是用左子树中的最大节点替代。
在右子树中找一个最小值，一定在右子树中的最左边；左子树中的最大值，一定在左子树的最右边。

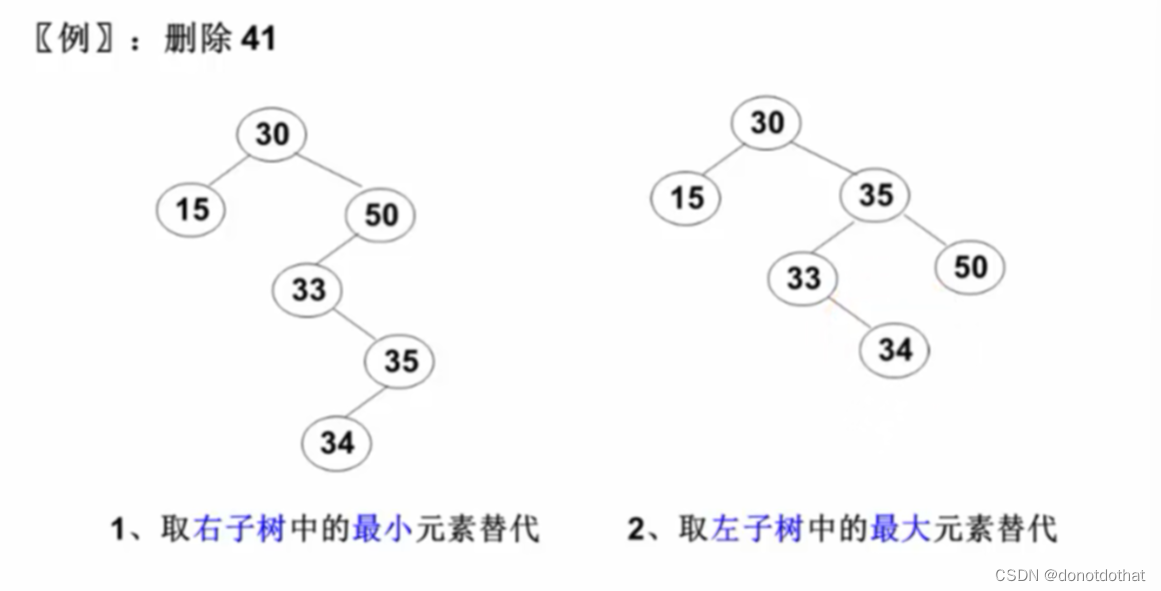
1. 首先通过查找找到41号节点；
2. 在41号结点的左右子树再次寻找，进行替代删除；
3. 41号结点为删除50号（使用查找的方法找到右子树的最小值），并且把41号节点的值赋值为50；
4. 改删除41号节点为删除35号（使用查找的方法找到），并且把41号结点的值赋值为35，并将34连接到上一层。
   因为转化成删除最大/最小节点一定不会有两个儿字节点，所以把这种情况转化为前两种情况。

BinTree Delete(int x,BinTree BST)//注意返回类型是树节点
{
	BinTree Temp;
	if( !BST )//首先对传入的结点进行判断
		printf("要删除的结点未找到");
	//先找到目标节点（要删除的结点）
	else if(x < BST->Data)//x小，向左子树进行递归
		BST->Left = Delete(x,BST->Left);
	else if(x > BST->Data)
		BST->Right = Delete(x,BST->Right);
	else //那这个情况就是BST->Data == x,找到对应的目标节点 
	{//因为目标结点的类型不同，删除的操作也不同，首先进行目标结点类型的判断：
		if(BST->Right && BST->Left)//如果目标节点左右子树均存在,那么就属于最复杂的那种
		{//进行替代删除，这里就选择右子树的最小值进行替代删除：
		Temp = FindMin(BST->Right);//找到右子树中的最小节点
		BST->Data = Temp->Data;//将右子树中的最小节点的值赋值给目标节点
		BST->Right = Delete(Temp->Data,BST->Right);//在目标节点的右子树中删除这个替代节点Temp	
		}
		else//左右子树至少其一不存在
		{
			Temp = BST;//先保存一下
		//将子节点接到上一次层：
			if( !BST->Right)//当目标节点只有左节点或者是叶节点（叶节点两子树为空，那么BST = NULL 也就是叶节点直接删除）
				BST = BST->Left;
			else//目标节点只有右节点
				BST = BST->Right;
			free(Temp);//释放目标节点
		}
	}
	return BST;//当每次函数的以上程序执行完成，函数唯一出口。从目标节点开始，逐一向前回溯，最后返回整个树的根节点
}

易错题目：

1. 若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最大值一定在叶结点上 错
   基于完全二叉树的特点，他是完美二叉树的截肢部分，那么最深右子树最大结点上还可以挂个左子树，他还是最大节点，但是他不是叶节点。因为要求是搜索树，还要保证顺序性。
   2)若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小值一定在叶结点上 对