Leetcode：669. 修剪二叉搜索树（C++）

news2024/11/29 22:38:38

问题描述：

实现代码与解析：

递归：

原理思路：

后序递归：

原理思路：

迭代：

原理思路：

问题描述：

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

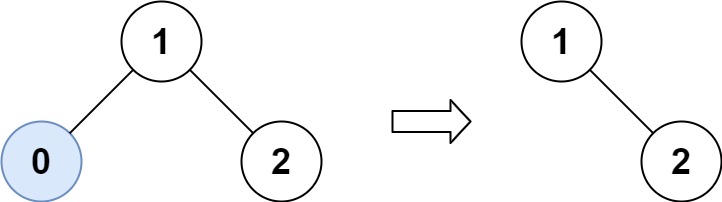
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

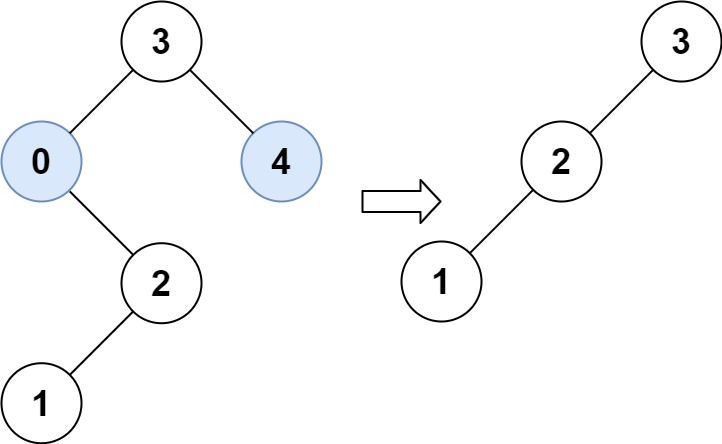
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

实现代码与解析：

递归：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) 
    {
        if(root==NULL) return NULL;
        if(root->val<low)
        {
            TreeNode* right=trimBST(root->right,low,high);
            return right;
        }
        if(root->val>high)
        {
            TreeNode* left=trimBST(root->left,low,high);
            return left;
        }
        root->right=trimBST(root->right,low,high);
        root->left=trimBST(root->left,low,high);
        return root;
    }
};

原理思路：

根据二叉搜索树的性质，在遍历到不在范围内的结点时：

若其小于下界，说明此结点的的左子树所有结点一定也小于下界，而此结点的右子树有可能会有在范围内的结点，所以我们向其右子树开始遍历。

若其大于上界，说明此结点的的右子树所有结点一定也大于上界，而此结点的左子树有可能会有在范围内的结点，所以我们向其左子树开始遍历。

还是不好理解的，大家最好还是模拟一下过程。

后序递归：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) 
    {
        if(root==NULL) return NULL;
        root->left=trimBST(root->left,low,high);
        root->right=trimBST(root->right,low,high);
        if (root->val < low) return root->right;
	    if(root->val>high) return root->left;
	    return root;
    }
};

原理思路：

此方法会好理解很多，但是运行时间会长一点，此方法会遍历所有的结点，而上一个方法是有方向的去修剪，不会遍历到所有结点。

此方法是从下向上处理的，所有不会存在左或右子树上存在任有不在范围内的结点，因为其子树已经处理过了，所以直接返回即可。

迭代：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) 
    {
        if (root==NULL) return NULL;
        //让root移动到范围内
        while (root != NULL && (root->val < low || root->val > high)) 
        {
            if (root->val < low) root = root->right; // 小于low向右走
            else root = root->left; // 大于high向左走
        }
        TreeNode *cur = root;
        // root已经在范围内，处理左孩子小于low的情况
        while (cur != NULL) {
            while (cur->left && cur->left->val < low) 
            {
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }
        cur = root;
        // 此时root已经在范围内，处理右孩子大于high的情况
        while (cur != NULL) {
            while (cur->right && cur->right->val >high) 
            {
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};