思路：
1.用动态规划，但是时间复杂度太高，效率太低
2.使用常规的DFS，时间复杂度高，包含了太多重复无效遍历，会超时
3.在DFS的基础上使用记忆化搜索，帮助消去重复的遍历，提高效率
原题链接：https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/description/

1.题目如下：

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

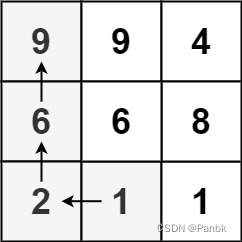
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 

解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

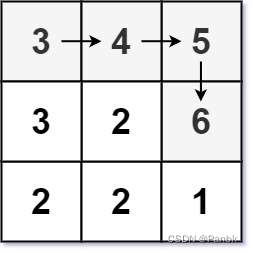
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 

解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1

2.代码如下：

class Solution {
    
public:
//思路一：动态规划  O(nm)
/*
    状态转移方程：
    dp[i][j]=max(dp[i'][j'] if matrix[i'][j'] > matrix[i][j]) + 1
    但是一个节点有四个移动方向，对于动态规划方程dp来说，找不到初始值供转移方程使用；
    可以将所有元素排序，从大到小遍历元素，并且使用转移方程，这样保证能够使用转移方程
    时间复杂度高  会超时
*/

//思路二：回溯法 BFS
/*
    如果只使用简单的BFS，则会超时，因为会有很多多余的重复的操作
*/
/*
    int maxLength=0;
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        vector<vector<int>> idx={{1,0},{-1,0},{0,1},{0,-1}};
        int n=matrix.size();
        int m=matrix[0].size();
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                stack<int> sTemp;
                backTrack(matrix,sTemp,i,j,idx);
            }
        }
        return maxLength;
    }

    void backTrack(vector<vector<int>>& matrix,stack<int> sTemp,int i,int j,vector<vector<int>> &idx){
        sTemp.push(matrix[i][j]);
        maxLength=maxLength<sTemp.size()?sTemp.size():maxLength;
        for(int k=0;k<4;k++){
            int inew=i+idx[k][0];
            int jnew=j+idx[k][1];
            if(inew>=0 && jnew>=0 && inew<matrix.size() && jnew<matrix[0].size()){
                if(sTemp.top()<matrix[inew][jnew]){
                    backTrack(matrix,sTemp,inew,jnew,idx);
                }
            }
        }

    }
*/


//思路三： DFS和 记忆化搜索提高效率
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        vector<vector<int>> idx={{1,0},{-1,0},{0,1},{0,-1}};
        //用来标记每个结点开始的所能达到的最大长度
        vector<vector<int>> mark(matrix.size(),vector<int>(matrix[0].size(),0));
        int n=matrix.size();
        int m=matrix[0].size();
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                //对于每个结点。取最大长度
                ans=max(ans,dfs(matrix,i,j,idx,mark));
            }
        }
        return ans;
    }

    int dfs(vector<vector<int>>& matrix,int i,int j,vector<vector<int>> &idx,vector<vector<int>>& mark){
        //如果不等于0，证明有其他路径经过该结点，直接返回路径
        if(mark[i][j]!=0){
            return mark[i][j];
        }
        //如果等于0，则证明未经过该结点，从该结点DFS，mark[][]++
        mark[i][j]++;
        for(int k=0;k<4;k++){
            int inew=i+idx[k][0];
            int jnew=j+idx[k][1];
            //DFS 条件
            if(inew>=0 && jnew>=0 && inew<matrix.size() && jnew<matrix[0].size() && matrix[inew][jnew]>matrix[i][j]){
                //如果有能够深度遍历的更大结点，则判断取两者更大值
                //如果一个结点没有能够遍历的结点，则mark[][]等于1；
                mark[i][j]=max(mark[i][j],dfs(matrix,inew,jnew,idx,mark)+1);
            }
        }
        return mark[i][j];
    }
    
};