基于二叉树的改进SPIHT算法（Matlab代码实现）

news2024/7/6 18:49:16

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

💥1 概述

文献来源：

随着现代社会越来越大量的信息需要存储和传输，通常会对这些信息进行压缩。人们不仅希望压缩算法有较高的压缩比，而且希望算法执行速度快。小波变换具有良好的时频局部表达能力和多分辨率分析特性，并有快速分解重构算法，在图像编码领域得到了广泛的应用。嵌入式零树编码算

法[1](Embedded Zerotree Wavelet, EZW)是一种基于小波变换的图像压缩算法，它通过不同尺度的小波系数在每个比特平面的空间相似性构造零树，从而用一个零树根成功地预测了大量非重要系数，取得了比基于离散余弦变换的 JPEG 更好的压缩效果。多级树集合分裂 (Set Partitioning in Hierarchical Trees, SPIHT)算法[2]对 EZW 算法做了重要改进，其具有更高的压缩效率、更快的执行速度等优点，是目前基于零树结构的压缩算法中的较优的算法[3]。SPECK(Set

Partitioning Embedded block)算法[4]加快了计算速度并进一步利用了子带内相连系数块的关系。

为取得更好的压缩效果，以上文献中几乎所有算法都需要进行无损压缩(熵编码)以便提高算法效率。然而，进行熵编码需要很大的计算量。如果在 SPIHT 算法中使用算术编码，编码时间将会多一倍以上[2]。为在保持 SPIHT 算法速度的同时改进压缩效果，本文提出一种新的基于 SPIHT 和二叉树的快速编码算法。该算法与上述文献不同，虽然文献[9]提出了一种基于提升小波的二叉树图像编码方法，不过此方法中的二叉树是一种和 SPIHT 的方向树类似的跨尺度的零树结构，而本文算法中的二叉树则建立在同一尺度的相邻系数上。

📚2 运行结果

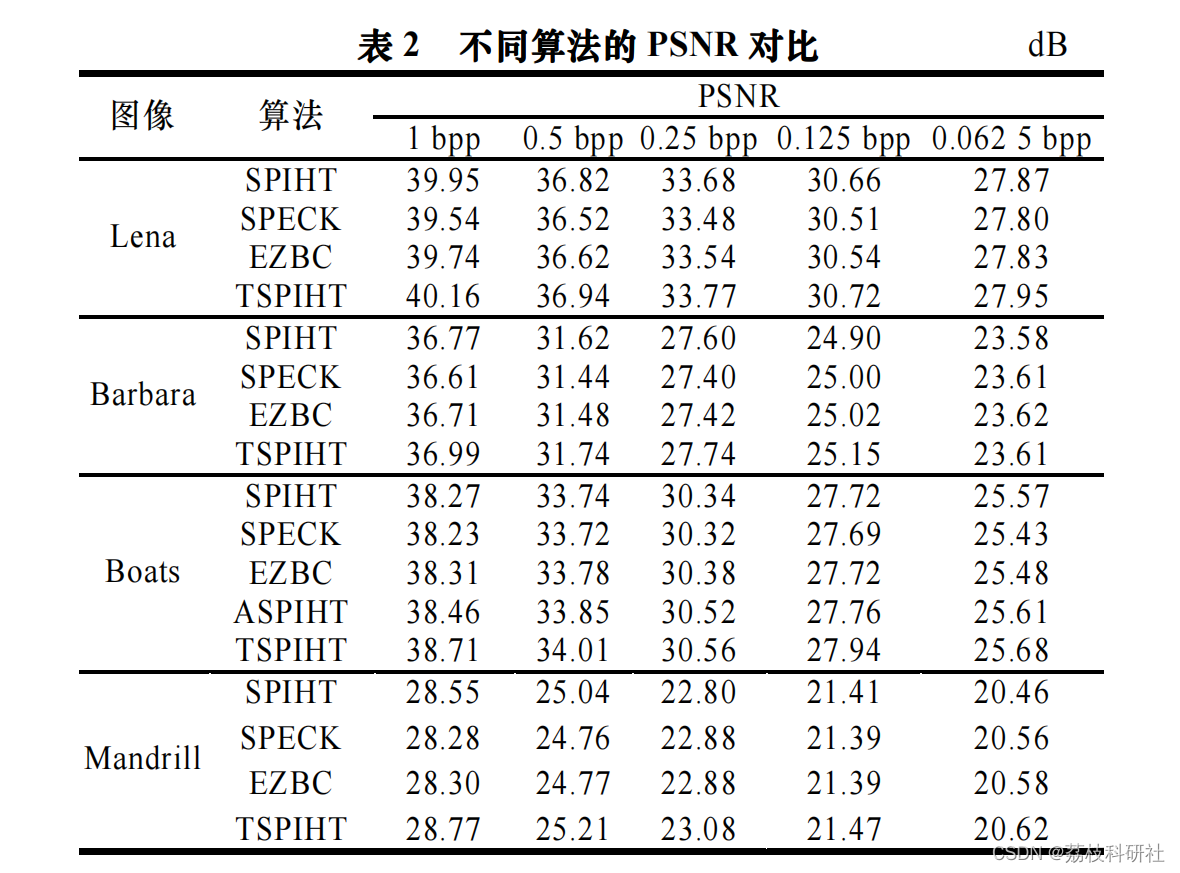
部分代码：

clc;clear;

%----------- Input ----------------

global level carow row

imname = 'img_lena.bmp';
Orig_I=double(imread(imname));

[row, col] = size(Orig_I);

% 最大比特率
rate = 1;
max_bits = floor(rate * row^2);

% 5个比特率下的编码长度[128:1, 64:1, 32:1, 16:1, 8:1]
brates = floor([0.0625, 0.125, 0.25, 0.5, 1]*row*row);

%----------- Wavelet Decomposition ----------------
n = size(Orig_I,1);
n_log = log2(n);

level = floor(n_log);
% level = 3;

carow = 2^(n_log-level);

I_W = wavecdf97(Orig_I, level);

n_max = floor(log2(abs(max(max(I_W)')))); % 初始阈值T=2^n_max

% =========================================================================
% Coding
[out_head,out_code,out_type,pixFlag] = func_SPIHT_Enc(I_W, max_bits, level);
l2 = find(out_code==2); out_code(l2)=[];
l2 = find(out_type=='O'); out_type(l2)=[];

% =========================================================================
% Decoding
disp(['aa_TSPIHT_' imname ' = [']);
img_dec = func_SPIHT_Dec(out_head,out_code,brates,Orig_I);
disp('];');

img_spiht = wavecdf97(img_dec, -level);
Q = 255;
MSE = sum(sum((img_spiht - Orig_I) .^ 2)) / row / col;
psnr = 10*log10(Q*Q/MSE);
rate = numel(Orig_I)*8/length(out_code);
disp([psnr,rate]);