前言

学习python数据结构与算法，学习常用的算法，
b站学习链接

74.AVL树的概念

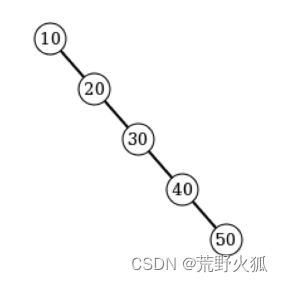
首先看一下二叉搜索树的效率
平均情况下，二叉搜索树进行搜索的时间为O(logn)
最坏情况下，二叉树可能非常偏斜，这样搜索时间就会是O(n)
在这里插入图片描述
解决方法：

随机化插入
AVL树
随机化插入有个问题，就是可能不是同一时间插入，同一时间插入随机化的话，可以像快速排序法那样，但隔一会插一个，隔一会插一个，最终插入形成的树还是可能斜偏。
AVL树可以较好解决这个问题，AVL是三个科学家提出的，AVL是三个的首字母。

AVL树:是一颗自平衡的二叉搜索树。
具有以下性质：

根的左右子树的高度之差的绝对值不能超过1
根的左右子树都是平衡二叉树
一上面那个斜二叉树举例，50的左右子树没有，都是0，40的左子树没有，右子树是1，绝对值就是1，30的左子树没有，右子树是2，高度之差绝对值就是2，就不满足平衡。

下面这颗树是AVL树，上面的数字是左子树的高度-右子树的高度，都满足条件。
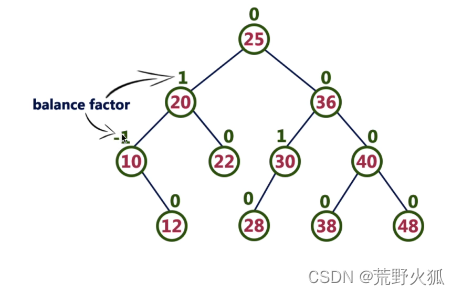
在这里插入图片描述
如果现在插入11，就是插到12的左子树，这样平衡就会打乱，需要树之间做一个平衡。这个平衡后面会讲。

75.AVL:旋转

插入一个节点可能会破坏AVL树的平衡，可以通过旋转来进行修正。
插入一个节点后，只有从插入节点到根节点的路径上的节点的平衡可能被改变。我们需要找出第一个破坏了平衡条件的节点，称之为K。K的两颗子树的高度差2。
不平衡的出现可能有4种情况

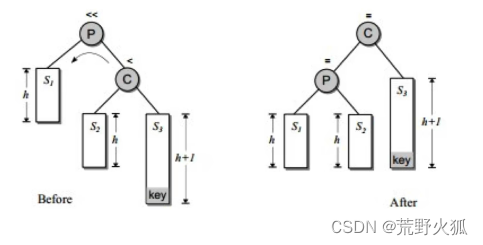
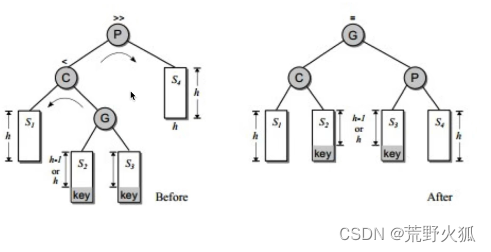
1.不平衡是由于对K的右孩子的右子树插入导致的：左旋
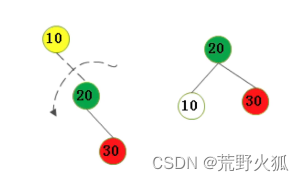
在这里插入图片描述
将10左旋到20的下方。
实际情况10，20，30带着好多子树，如下S3本来的是h高度，插入Key之后，高度加1，导致不平衡，
把P左旋到C的下方，连接S1,S2。

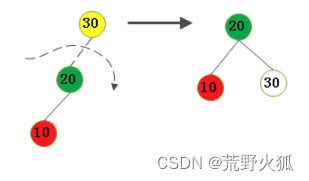
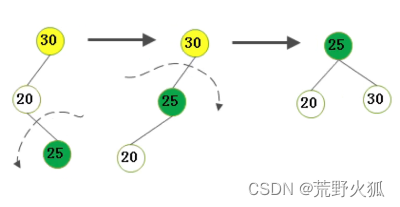
2.不平衡是由于对K的左孩子的左子树插入导致的：右旋

把30右旋到下面
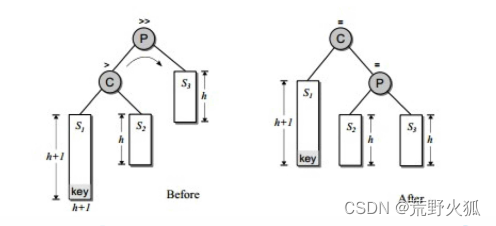
在这里插入图片描述
和左旋类似，把P右旋到C的下面

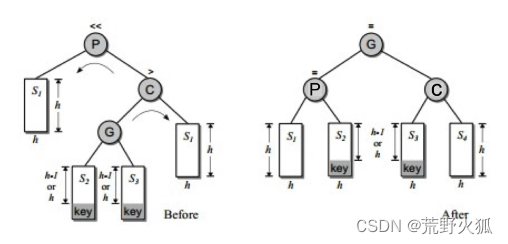
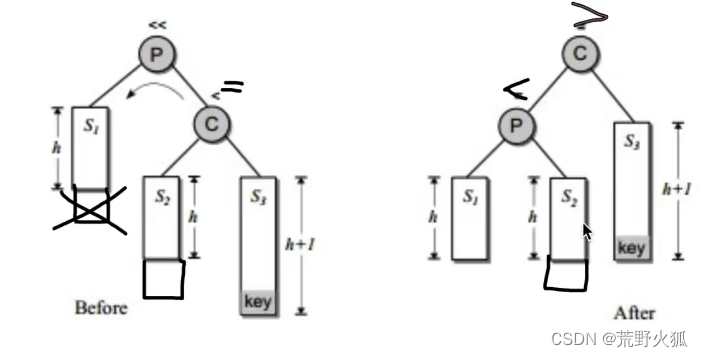
3.不平衡是由于对K的右孩子的左子树插入导致的：右旋-左旋

先把20右旋到下面，再把10左旋到下面

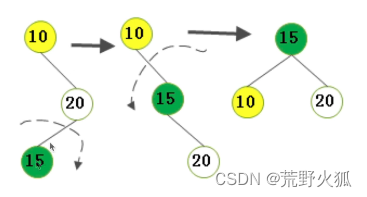
在这里插入图片描述
对P的右孩子C的左子树G插入，S2和S3本来的h-1,在S2或者S3插入一个后发生不平衡。先将C右旋到G的下方，再将P左旋到G的下方。

在这里插入图片描述
4.不平衡是由于对K的左孩子的右子树插入导致的：左旋-右旋

和上一个做一个镜像差不多。

在这里插入图片描述

四种方法挺好记的
左左右
右右左
左右左右
右左右左

76.AVL:旋转实现1

根据上面的图写出左旋和右旋。平衡因子balance factor 这里选右子树-左子树，
在这里插入图片描述

这里注意
插入时旋转没有问题，可是右右或者左左删除导致的不平衡，bf就不是0了，
比方说s1,s2,s3本来都是h+1的高度，删除s1中的一个key,左旋，最后p.bf=0-1=-1,c.bf=(h+2)-(h+1)=1。

在这里插入图片描述

77.AVL:旋转实现2

对照之前的图写出右旋-左旋
在这里插入图片描述
镜像写出，左旋-右旋

78.AVL:插入

主要一个点是：从父亲节点往上找
直到更新到一个节点的bf(平衡因子)是0后就不再更新
如果是+1或-1则继续下一个更新，-2或2则判断此时类型，进行响应的旋转。
总的代码如下，类继承了之前的二叉树，在此之上写的AVL树和节点

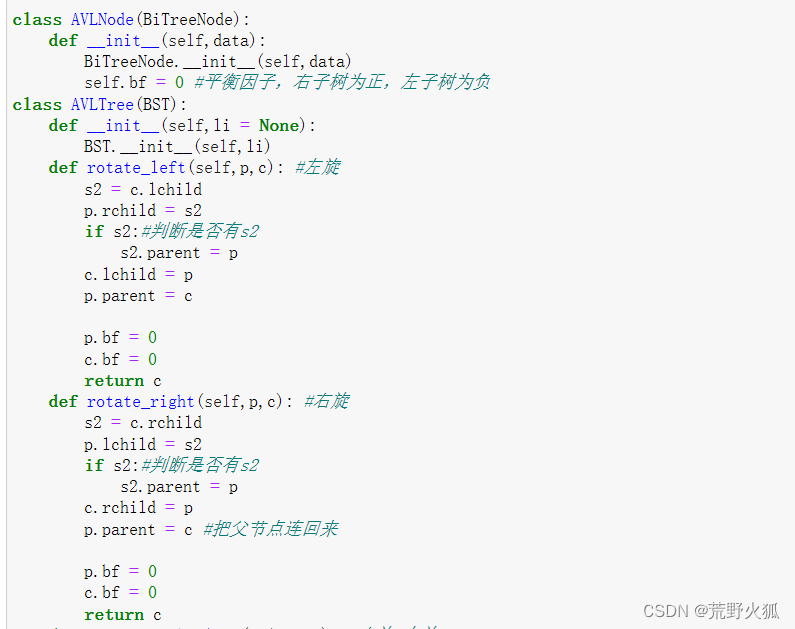
class AVLNode(BiTreeNode):
    def __init__(self,data):
        BiTreeNode.__init__(self,data)
        self.bf = 0 #平衡因子，右子树为正，左子树为负
class AVLTree(BST):
    def __init__(self,li = None):
        BST.__init__(self,li)
    def rotate_left(self,p,c): #左旋
        s2 = c.lchild
        p.rchild = s2
        if s2:#判断是否有s2
            s2.parent = p
        c.lchild = p
        p.parent = c
        
        p.bf = 0
        c.bf = 0
        return c
    def rotate_right(self,p,c): #右旋
        s2 = c.rchild
        p.lchild = s2
        if s2:#判断是否有s2
            s2.parent = p
        c.rchild = p
        p.parent = c #把父节点连回来
        
        p.bf = 0
        c.bf = 0
        return c
    def rotate_right_left(self,p,c): #右旋-左旋
        g = c.lchild
        #右旋
        s3 = g.rchild
        c.lchild = s3
        if s3:#判断是否有s3
            s3.parent = c
        g.rchild = c #连回去
        c.parent = g
        #左旋
        s2 = g.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        g.lchild = p
        p.parent = g
        
        #更新bf
        if g.bf >0: # 插到s3 
            p.bf = -1
            c.bf = 0
        elif g.bf <0: #插到s2
            p.bf = 0
            c.bf = 1
        else: #插入的是g
            p.bf = 0
            c.bf = 0
        return g
    def rotate_left_right(self,p,c):#左旋-右旋
        g = c.rchild
        
        s2 = g.lchild
        c.rchild = s2
        if s2:
            s2.parent = c
        g.rchild = c
        c.parent = g
        
        s3 = g.lchild
        p.rchild = s3
        if s3:
            s3.parent = p
        g.rchild = p
        p.parent = g
        
        #更新bf
        if g.bf <0: # 即插到s2
            p.bf = 1
            c.bf = 0
        elif g.bf >0: #插到s3
            p.bf = 0
            c.bf = -1
        else: #插入的是g
            p.bf = 0
            c.bf = 0   
        return g
    def insert_no_rec(self,val):
        #1.和BST一样，先插入
        p = self.root
        if not p:#如果是空树
            self.root = AVLNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:  #如果左子树存在，则根节点为这颗左树的根
                    p =p.lchild 
                else:#左孩子不存在,就插到这个位置上
                    p.lchild = AVLNode(val)
                    p.lchild.parent = p
                    node = p.lchild  #node存储的是插入的节点
                    break
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = AVLNode(val)
                    p.rchild.parent = p
                    node = p.rchild  ##
                    break
            else:   # val ==p.data值就等于这个值，就相当于 插第二遍这个值，不允许插return
                return 
        
        #2.更新balanc factor
        while node.parent: #node.parent 不空，一直循环到根节点
            if node.parent.lchild == node: #如果是左子树来的，左子树更沉了
                #更新node.parent的bf -= 1 #选择左边-1 #右边+1 的平衡方法
                if node.parent.bf <0: #原来的node.parent.bf == -1,现在要更新后变为-2
                    #做旋转 
                    #看node哪边沉
                    g = node.parent.parent  #为了连接旋转之后的子树
                    x = node.parent   #旋转前子树的根
                    if node.bf >0: #如果是右边沉 #左孩子的右子树
                        n = self.rotate_left_right(node.parent,node) #具体更新函数里有
                    else: #如果左边沉 左左 - 右
                        n = self.rotate_right(node.parent,node)
                        #记得：把n和g连起来
                elif node.parent.bf >0: #原来node.parent.bf = 1 ,现在要更新后变为0
                    node.parent.bf = 0
                    break
                else: #原来node.parent.bf = 0 更新之后变为-1
                    node.parent.bf = -1
                    node = node.parent #往父一级更新
                    continue
                
            else:# 传递是从右子树传来的，右子树更沉了
                #更新node.parent的bf += 1 
                if node.parent.bf >0: #原来的node.parent.bf == 1,现在要更新后变为2
                    #做旋转 
                    #看node哪边沉
                    g = node.parent.parent  #为了连接旋转之后的子树
                    x = node.parent   #旋转前子树的根
                    if node.bf <0: #如果是左边沉 #右孩子的左子树 -右左
                        n = self.rotate_right_left(node.parent,node) #具体更新函数里有
                    else: #如果右边边沉 右右 - 左  
                        n = self.rotate_left(node.parent,node)
                    #记得连起来
                elif node.parent.bf <0: #原来node.parent.bf = -1 ,现在要更新后变为0
                        node.parent.bf = 0
                        break
                else: #原来node.parent.bf = 0.更新之后变为1
                        node.parent.bf = 1
                        node = node.parent #往父一级更新
                        continue
            # 连接旋转后的子树
            n.parent = g
            if g: #g不是空  #旋转之后node.parent 已经不是原来的parent了所以用x保存一下
                if x == g.lchild: #判断是根左子树连还是右子树连
                    g.lchild = n
                else:
                    g.rchild = n
                break #只可能是旋转后进入这里
            else: #g是空 n本身是根节点
                self.root = n 
                break

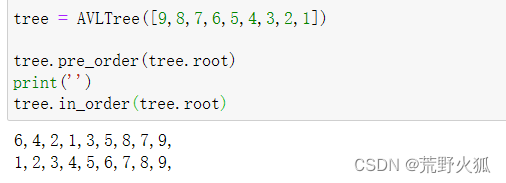
插入后如下，中序遍历依旧是升序
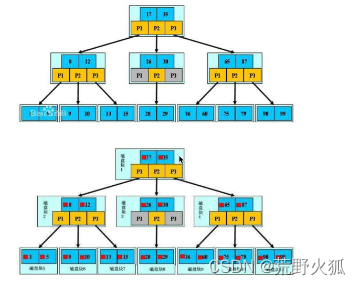
在这里插入图片描述