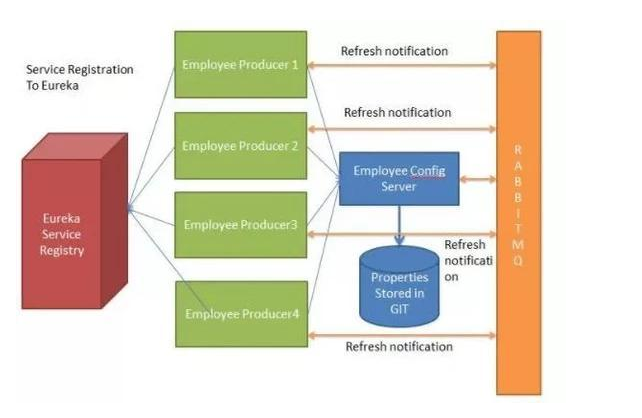
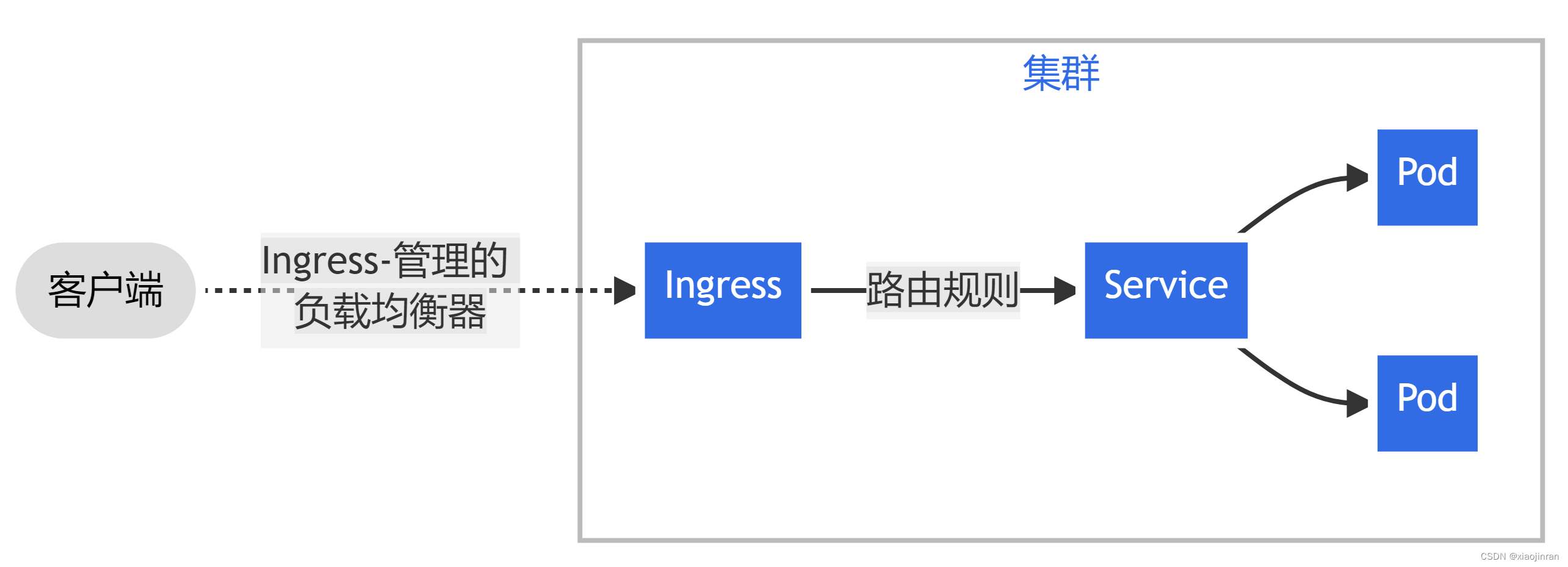
文章目录
- 1. 卡方检验
- 2. 费希尔精确检验(Fisher Exact Test)
- 3. Cochran-Mantel-Haenszel检验
独立性检验:用来判断变量之间相关性的方法,如果两个变量彼此独立,那么两者统计上就是不相关的
1. 卡方检验
可以使用chisq.test()函数对二维表的行变量和列变量进行卡方独立性检验,具体的数学问题不在这里讨论。
数据是二维的列联表
以吸烟与性别是否有关系举例,卡方检验的假设检验是:
(1) 零假设(H0):吸烟和性别不相关(也就是独立)。
(2) 备择假设(H1):吸烟和性别相关(也就是有关系)。
(3) 检验水准:alpha=0.05
用chisq.test()函数算出的P-value值 > 0.05,即接受H0,吸烟和性别不相关(也就是独立)
P-value值 < 0.05,即拒绝H0,接受H1。吸烟和性别相关(也就是有关系)
例子:
A <- c(rep("male",15),rep("female",20),rep("male",15))# 创建变量A
B <- c(rep("healthy",4),rep("sick",35),rep("healthy",11)) # 创建变量B
C <- c(rep("smoker",26), rep("nonsmoker",24)) # 创建变量C
mydata <- data.frame(A,B,C) # 利用以创建的变量构建数据框
mytable <- table(A,C) #生成二维频数表
chisq.test(mytable) #卡方检验判断A和B的相关性


以alpha=0.05的检验水准来看,由于p-value > 0.05,即接受H0,吸烟和性别不相关(也就是独立)
注意:
卡方检验要求列联表中每格的数值或者期望值大于5,如果该条件不满足,那么R中就会使用 Yate 's矫正公式进行计算。
2. 费希尔精确检验(Fisher Exact Test)
费希尔精确检验是一个基于超几何分布的检验变量间独立性的方法,在R语言中可以直接使用 fisher.test( )
数据是二维的列联表
例子:
A <- c(rep("male",15),rep("female",20),rep("male",15))# 创建变量A
B <- c(rep("healthy",4),rep("sick",35),rep("healthy",11)) # 创建变量B
C <- c(rep("smoker",26), rep("nonsmoker",24)) # 创建变量C
mydata <- data.frame(A,B,C) # 利用以创建的变量构建数据框
mytable <- table(A,C) #生成二维频数表
fisher.test(mytable)

在R中输出的结果有p值、备择假设、95%置信区间、OR值,从结果来看p-value>0.05, 说明吸烟和性别不相关,这个结论和卡方检验的结果一致。
3. Cochran-Mantel-Haenszel检验
主要针对的是分层数据,它的零假设是两个分类变量在调整组间差异后是彼此独立的,他们之间是没有其它的交互作用。在R语言中我们可以通过mantelhaen.test(x) 函数来实现,这里x通常是一个三维数据表。
例子:
A <- c(rep("male",15),rep("female",20),rep("male",15))# 创建变量A
B <- c(rep("healthy",4),rep("sick",35),rep("healthy",11)) # 创建变量B
C <- c(rep("smoker",26), rep("nonsmoker",24)) # 创建变量C
mydata <- data.frame(A,B,C) # 利用以创建的变量构建数据框
mytable <- table(C, B, A) #将性别作为调整的因素
mytable
mantelhaen.test(mytable)

从上面的结果可以看出,以alpha=0.05为检验水准时,p-value <0.05 说明在矫正性别之后吸烟和健康有关,同时依据OR值大于1可以说明吸烟是健康的危险因素。