目录
前言
1、插入排序
实例
2、选择排序
实例
3、冒泡排序
实例
前言
声明:本文所有动图来源为菜鸟教程
🍀作者简介:被吉师散养、喜欢前端、学过后端、练过CTF、玩过DOS、不喜欢java的不知名学生。
🍁个人主页:红中
🍂不就是蓝桥杯嘛,干他!!我堂堂
来说说简单排序
简单排序一共分为三种
- 插入排序
- 选择排序
- 冒泡排序
1、插入排序
那么首先介绍下插入排序的原理,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。

实例
1list = list(map(int,input().split(',')))
2for i in range(1,len(list)):
3 for j in range(0,i):
4 if list[i]<list[j]:
5 z=list[i]
6 list.pop(i)
7 list.insert(j,z)
8 break
9
10print(list)
简单解释下,第一行通过input传入字符串数据,后面加上split(',')是使用逗号进行分割,若题目未明确要求,可以使用空格替代逗号
接下来使用map函数,将传入的数据转换成int类型
通过list构建列表
外层的循环通过变量i来进行迭代,此处使用len()获取由传入数据构建出的列表的长度作为迭代次数的终止值
那实际上,这个循环的目的就是针对从第二个/第1位开始的每个数据
通过第二个循环来进行比较这个数据和他前面的数据的大小关系
那么这里我们也可以看到,因为是和前一个数据去比较,第一个/第0位数据前面是没有东西的, 所以,我们外层循环的迭代,是从第二个/第一位数据开始的
那第二个循环的迭代有什么含义呢,可以看到使用的是变量j进行迭代,从第0位数据迭代到第i位
接下来使用if进行判断,
list[i]<list[j]如果我要判断的第i位数据,小于它前面第j位的数据,那就先使用一个新变量把第i位的值保存下来,再用pop()函数弹出list[i],接下来通过insert方法,将其插入到第j位数据的前面,使保存list[i]的值的变量z,出现在第j位然后退出内层循环,开始对第i+1位数据进行判断,以此类推
2、选择排序
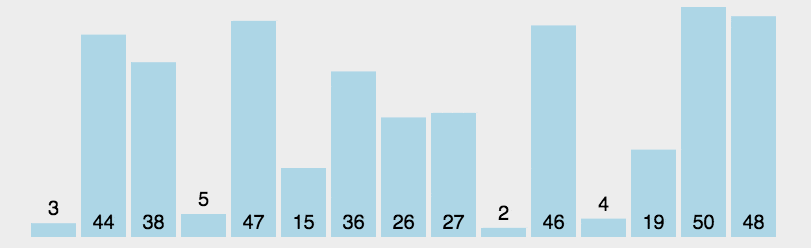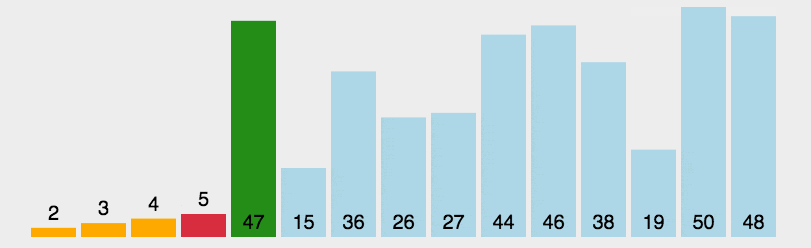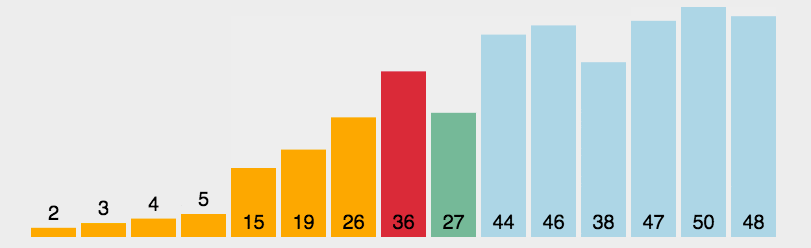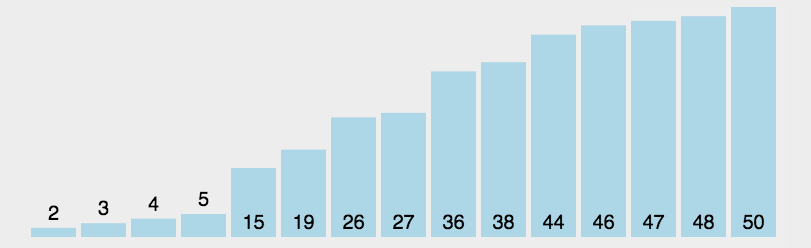
通过动图可以看出,本算法的原理是为找出列表中最大/最小的值,然后将其与最左/最右的数据进行换位,来实现排序
实例
list = list(map(int,input().split(',')))
for i in range(len(list)):
min_num=i
for j in range(i+1,len(list)):
if list[j]<list[min_num]:
min_num=j
list[i],list[min_num]=list[min_num],list[i]
print("排序后为:")
for i in range(len(list)):
print("%d"%list[i])
简单来看一下,第一行不多说了,和刚才一样
外层循环也是
发现有个新变量哈——min_num,这个变量专门用来存储数据中最小的值对应的位数
在初始阶段,我们将最小值设定为第一个/第0位对应的数据
接下来看第二个循环,它迭代的范围是从i后面的第一位数据到列表的最后一位数据
如果发现后面有比他更小的,就将min_num中对应的位数换成第j位
当然,因为这个时候才刚刚进行第一次判断,所以不能更改其值,min_num=j只是暂时存储
那么注意缩进哈
list[i],list[min_num]=list[min_num],list[i]此处的代码看缩进可以很容易看出来,他并不属于第二个for内部
也就是,它是在if语句执行完一轮后才通过python特有的形式来进行交换两处的值
3、冒泡排序
吐槽一句,才发现冒泡排序原来这么呆
原理就是它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换
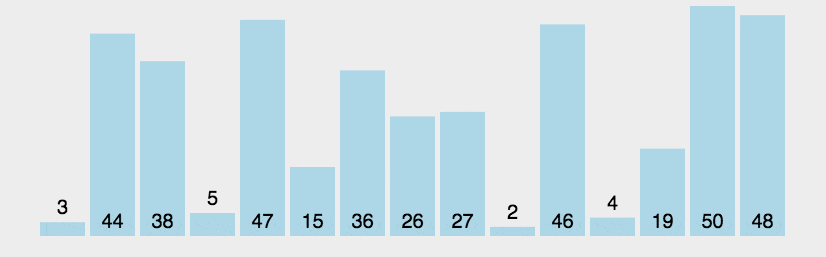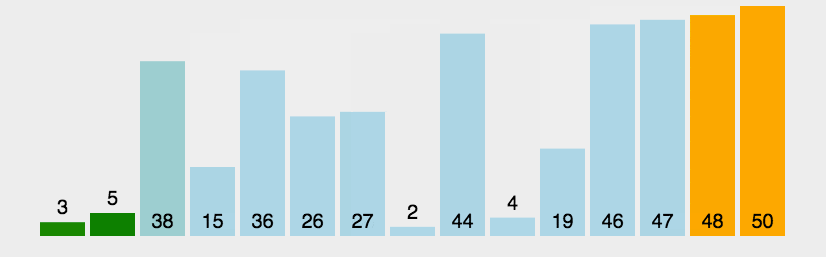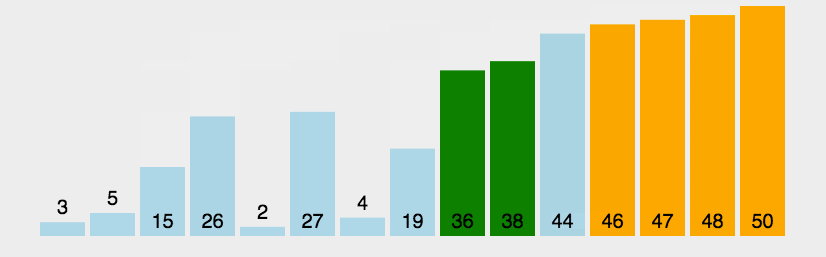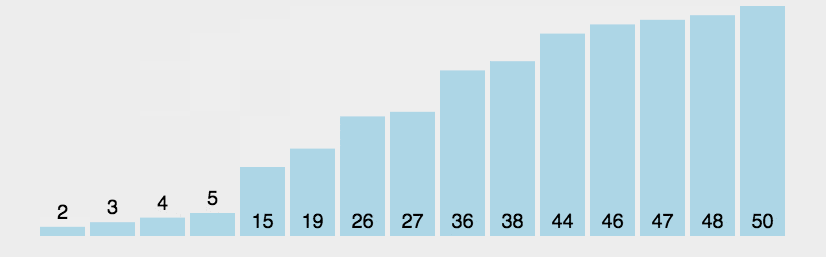
实例
def hongzhong(list):
m = len(list)
for i in range(m):
for j in range(0,m-i-1):
if list[j+1]<list[j]:
list[j],list[j+1] = list[j+1],list[j]
list = list(map(int,input().split(',')))
hongzhong(list)
print("排序后的列表:")
for i in range(len(list)):
print("%d"%list[i])
看起来相对于其他两种有点复杂
别慌
首先定义了一个叫hongzhong的函数,里面通过变量m存储列表长度
最外层循环的目的是遍历整个列表中的元素
内层循环需要讲的只有一点
就是
for j in range(0,m-i-1):这里为什么是总长度m减去当前长度i再减一
可以看到
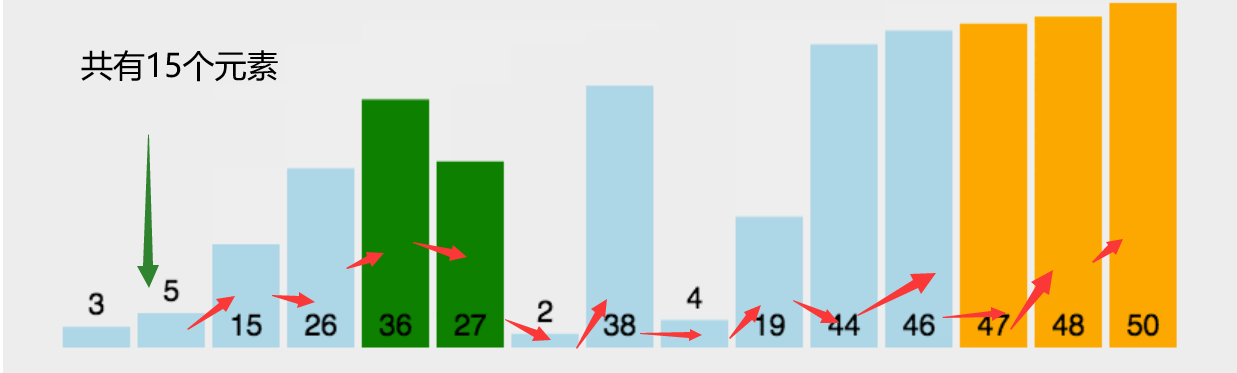
假设我们从第二个开始,那么需要剩下元素的个数就是15-2
所以需要比较的次数,就是15-2-1
由此推得
其余不过多赘述