一、麦轮原理
麦克纳姆轮:简称麦轮,由轮毂和围绕轮毂的辊子组成。
辊子:没有动力的从动小滚轮。
麦克纳姆轮辊子轴线和轮毂轴线夹角是45度。
A轮(左旋)与B轮(右旋)互为镜像关系


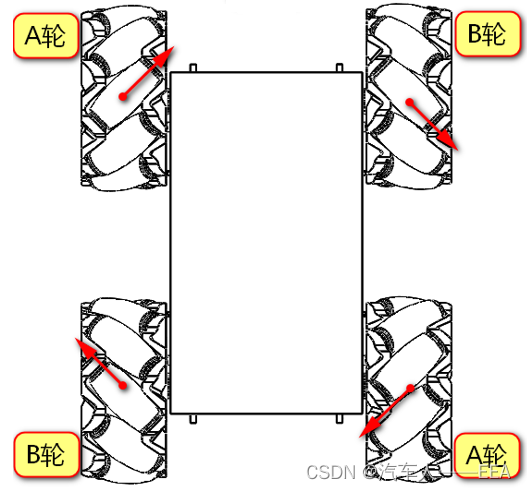
麦轮在车上的分布:(“外八”,AB对角安装)
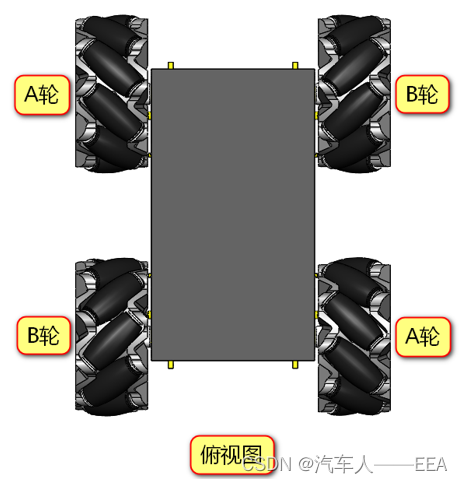
地面投影:(“内八”)
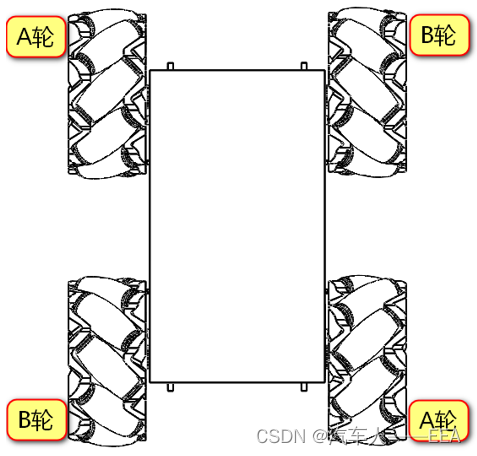
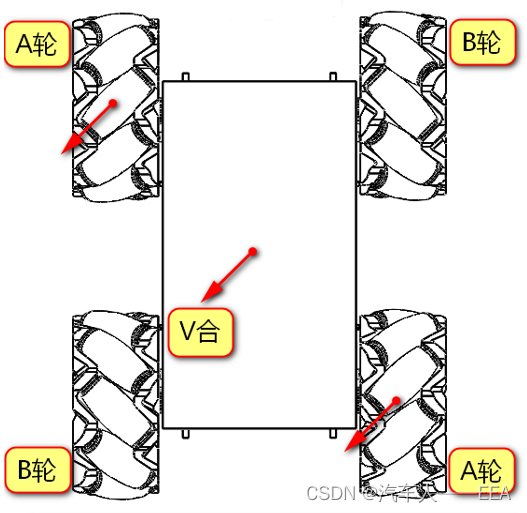
1.前进:(AB轮可以相互抵消轴向速度,正转:沿辊子轴向上;反转:沿辊子轴向下)
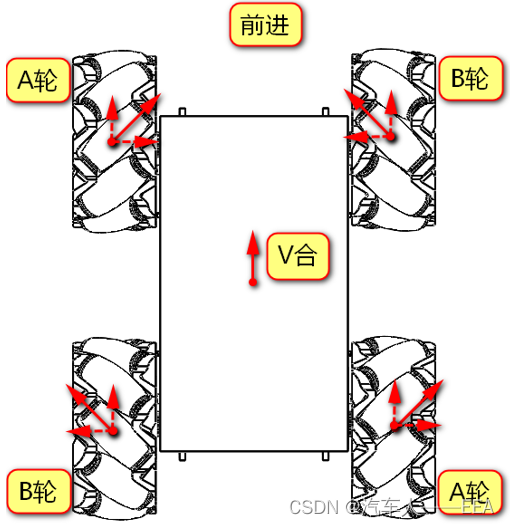
2.倒退:(AB轮可以相互抵消轴向速度)
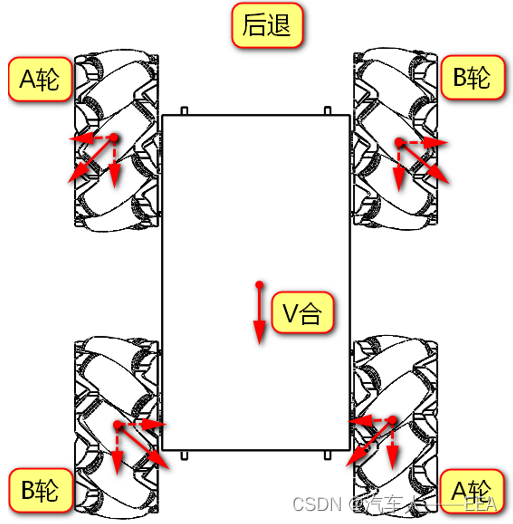
3.左移:(A轮反转,B轮正转)
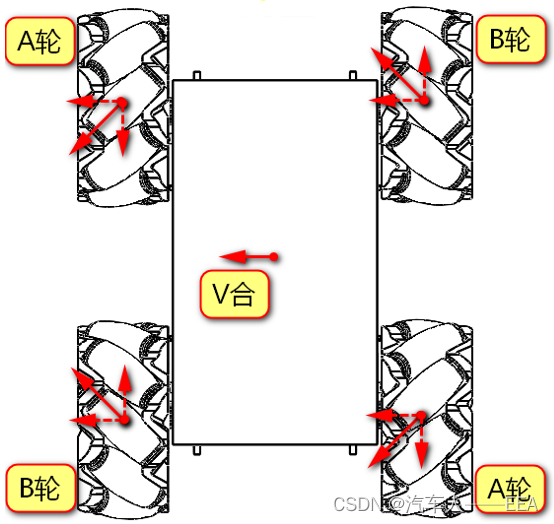
4.右移:(A轮正转,B轮反转)
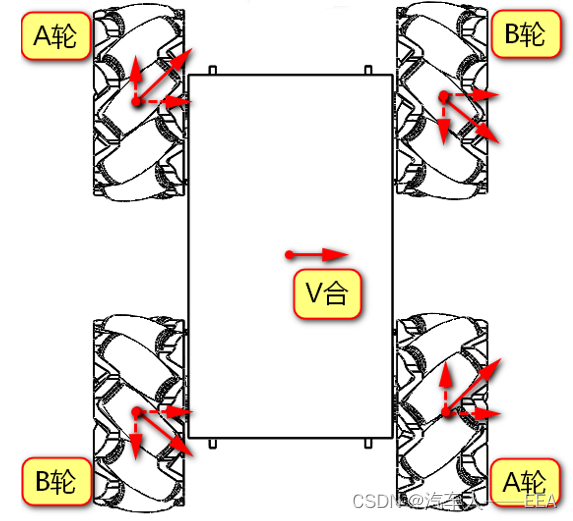
4.原地左转掉头:(左前:反转;右前正转;左后:反转;右后:正转。即同侧左:反转;同侧右:正转)

5.原地右转掉头:(左前:正转;右前反转;左后:正转;右后:反转。即同侧左:正转;同侧右:反转)
6.左前(对角B轮:正转,对角A轮:不转)

7.右前(对角A轮:正转,对角B轮:不转)

8.左后(对角A轮:反转,对角B轮:不转)
9.右后 (对角B轮:反转,对角A轮:不转)

10.绕前轴中心左转(前轴A、B轮:不转;后轴B轮:反转,A轮:正转)
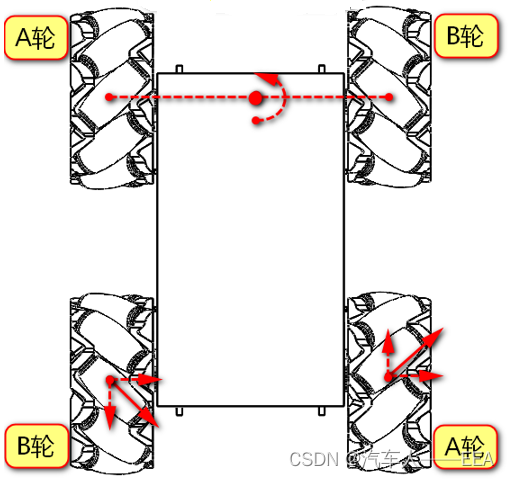
11.绕前轴中心右转 (前轴A、B轮:不转;后轴B轮:正转,A轮:反转)
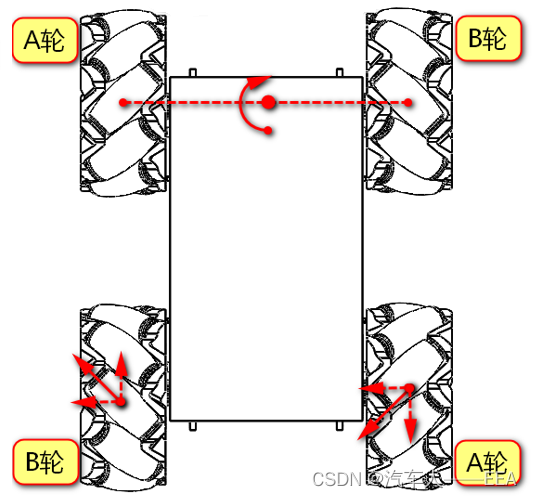
12.绕后轴中心左转(后轴A、B轮:不转;前轴B轮:正转,A轮:反转)
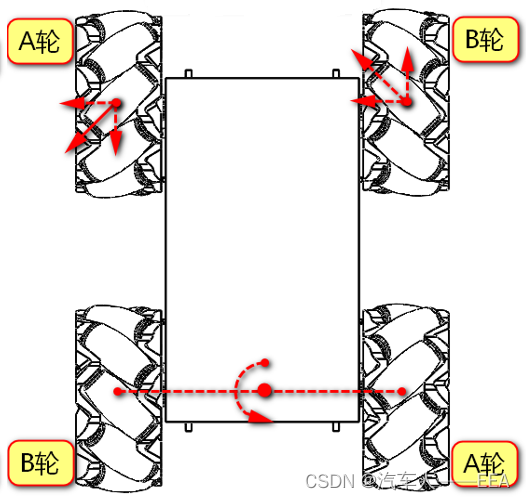
13.绕后轴中心右转(后轴A、B轮:不转;前轴B轮:反转,A轮:正转)

| 运动方向 | 左前——A轮 | 右前——B轮 | 左后——B轮 | 右后——A轮 |
| 前进 | 正转 | 正转 | 正转 | 正转 |
| 倒退 | 反转 | 反转 | 反转 | 反转 |
| 左移 | 反转 | 正转 | 正转 | 反转 |
| 右移 | 正转 | 反转 | 反转 | 正转 |
| 原地左转掉头 | 反转 | 正转 | 反转 | 正转 |
| 原地右转掉头 | 正转 | 反转 | 正转 | 反转 |
| 左前 | 不转 | 正转 | 正转 | 不转 |
| 右前 | 正转 | 不转 | 不转 | 正转 |
| 左后 | 反转 | 不转 | 不转 | 反转 |
| 右后 | 不转 | 反转 | 反转 | 不转 |
| 绕前轴中心左转 | 不转 | 不转 | 反转 | 正转 |
| 绕前轴中心右转 | 不转 | 不转 | 正转 | 反转 |
| 绕后轴中心左转 | 反转 | 正转 | 不转 | 不转 |
| 绕后轴中心右转 | 正转 | 反转 | 不转 | 不转 |