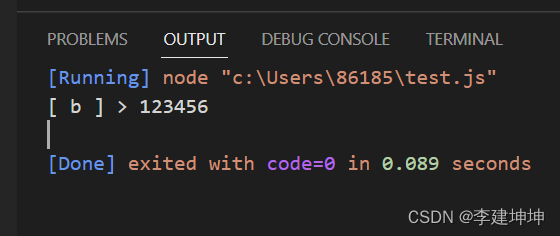
问题描述

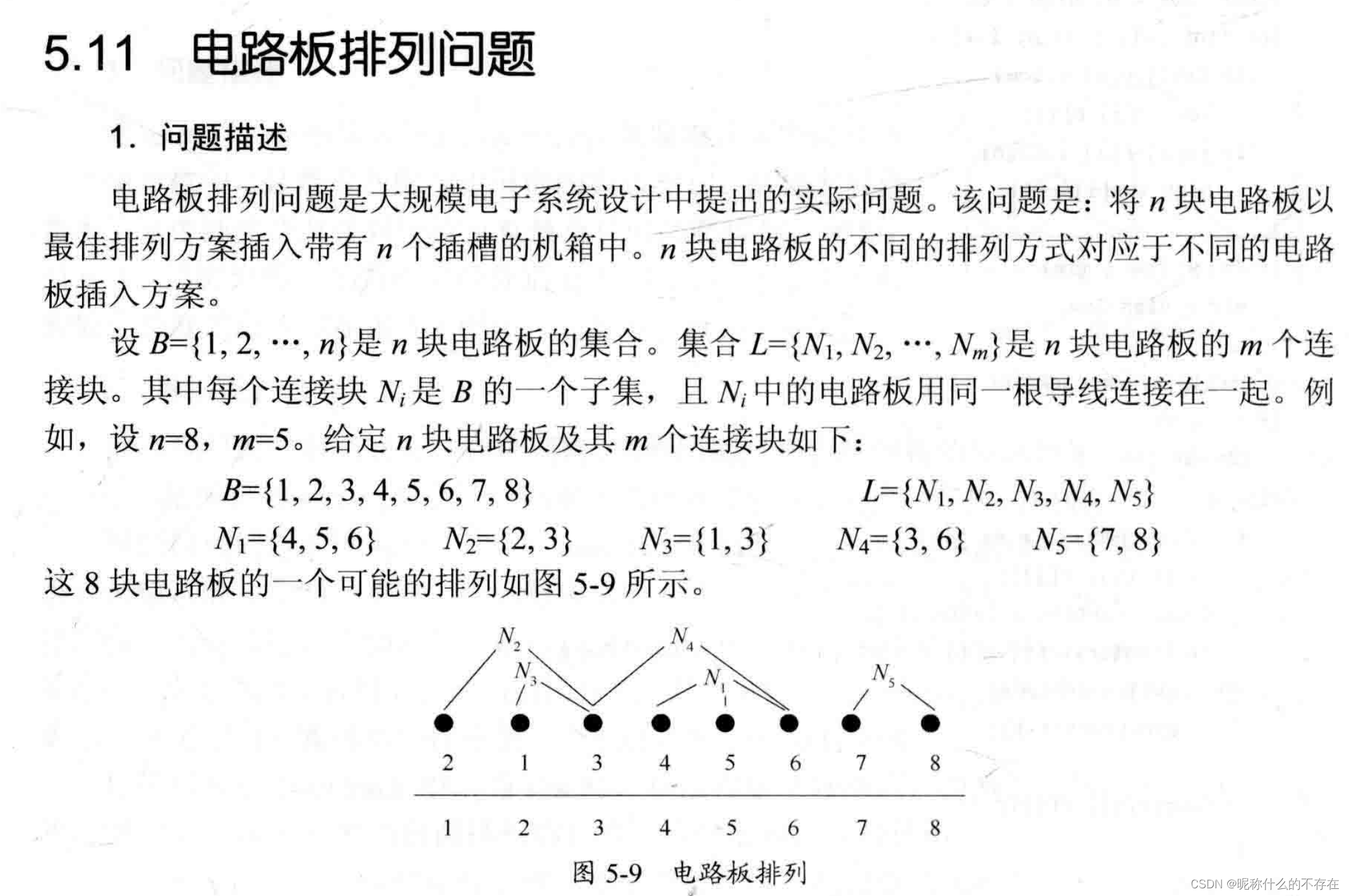
将n块电路板以最佳排列插入带有n个插槽的机箱中，要求对于给定的电路板连接块，确定最佳排列，使其具有最小的密度。设x[ ] 表示n块电路板的一个排列，x[ i ]表示在机箱的第 i 个插槽中插入电路板x[ i ]，x确定的电路板排列密度定义为：跨越相邻线路板插槽的最大连接数。如图5-9，这种电路板排列方案的密度为2。

问题分析

电路板的最佳排列问题的解空间是典型的排列树。分清电路板和连接块这两个概念。

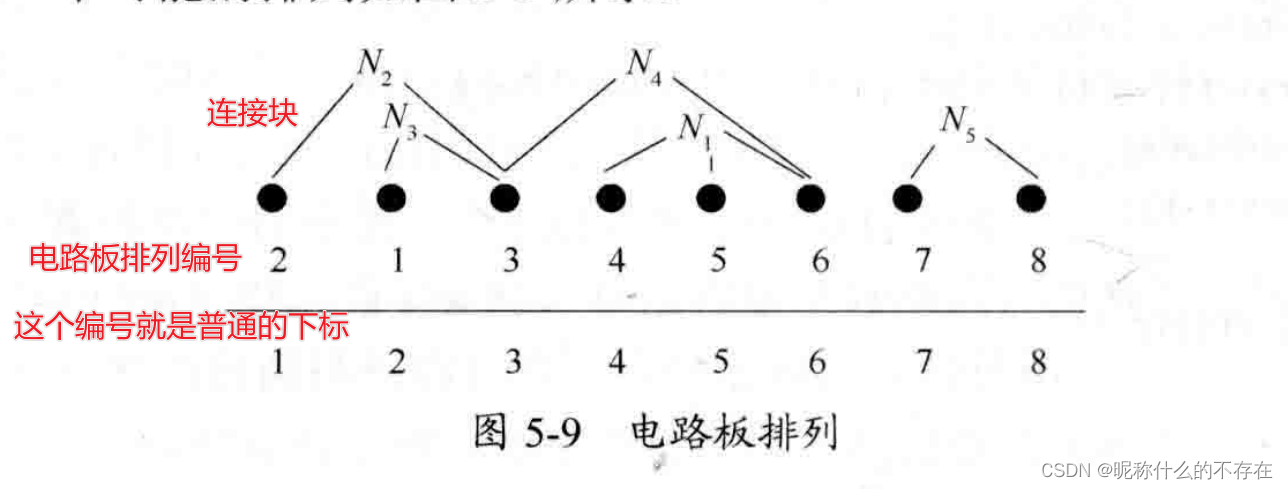
首先定义初始化变量

输入：int B[n][n]表示输入，B[i][j]=1表示电路板 i 在连接块 j 中

int total[ j ]是连接块Nj的电路板数量，就是这个连接块跨越了多少个电路板

电路板当前排列方案记录在x[1:i]中，当前解

now[j]表示在x[1:i]中包含的连接块Nj中的电路板的数量，这个用来判断插槽 i 和 i+1之间的连线数量，如果连接块Nj的连线跨越插槽 i 和 i+1 ，那么now[ j ] ！= total[ j ] && now[ j ] >0

然后就是最有解的一些变量，bestx[ ] 数组存放最优解，bestd表示最优密度

回溯主函数

伪代码

完整代码

#include <iostream>
#include <cstring> //memset头文件
#include <string.h>
using namespace std;
#define MAX 10

int x[MAX];        //当前电路板排列
int bestx[MAX];    //最优电路板排列
int n;             //电路板个数
int bestd = 10000; //最优密度，电路板密度为跨越相邻电路板最多连线数
int m;             //连接块数
int total[MAX];    // total[j]表示连接块j中电路板的个数
int now[MAX];      // now[j]表示当前解下，连接块j中电路板的个数
int b[9][6];       //连接块数组

void swap(int &a, int &b){
    int temp = a;
    a = b;
    b = temp;
}

//搜索排列树
//第i个电路板，当前排列密度为cd
void backtrack(int i, int cd){
    if (i == n) //当到达叶结点
    {
        bestd = cd; //算法仅完成比当前解更优的解，所以cd肯定优于bestd
        cout << "bestd= " << bestd << endl;
        memcpy(bestx, x, sizeof(x)); //拷贝最优解向量
    }
    else{
        for (int j = i; j <= n; j++) //下一步选哪个电路板
        {
            //计算增加了电路板x[j]后的连线密度
            int ld = 0;
            for (int k = 1; k <= m; k++)
            {
                now[k] += b[x[j]][k];                 //计算当前包含在连接块k中的电路板个数
                if (now[k] > 0 && now[k] != total[k]) //满足此条件
                    ld++;                             //连线密度增加
            }
            if (cd > ld) //更新ld
                ld = cd;
            if (ld < bestd) //如果当前连线密度小于最优值，才可能产生最优值，搜索子树
            {
                swap(x[i], x[j]);
                cout << "ninininini" << endl;
                backtrack(i + 1, ld); //搜索下一个结点
                swap(x[i], x[j]);
            }
            //恢复状态，为返回上一层做准备
            for (int k = 1; k <= m; k++)
            {
                now[k] -= b[x[j]][k];
            }
        }
    }
}

int main(){
    n = 8; //电路板数
    m = 5; //连接块数
    //初始化的输入矩阵信息
    b[9][6] = {
        {0, 0, 0, 0, 0, 0},
        {0, 0, 0, 1, 0, 0},
        {0, 0, 1, 0, 0, 0},
        {0, 0, 1, 1, 1, 0},
        {0, 1, 0, 0, 0, 0},
        {0, 1, 0, 0, 0, 0},
        {0, 1, 0, 0, 1, 0},
        {0, 0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0, 1}};
    memset(now, 0, sizeof(now));
    memset(total, 0, sizeof(total));
    //初始化x为单位排列并计算total
    for (int i = 1; i <= n; i++)
    {
        x[i] = i;
        for (int j = 1; j <= m; j++)
            total[j] += b[i][j];
    }

    backtrack(1, 0);

    printf("电路板个数：%d\n", n);
    printf("连接块个数：%d\n", m);
    printf("连接块情况：\n");
    printf("N1={4,5,6},N2={2,3},N3={1,3},N4={3,6},N5={7,8}\n");
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
            printf("%d ", b[i][j]);
        printf("\n");
    }
    printf("最优密度为：%d\n", bestd);
    printf("最优排列为：\n");
    for (int i = 1; i <= n; i++)
        printf("%d ", bestx[i]);
    printf("\n");
    return 0;
}