参考代码：BEVDepth

1. 概述

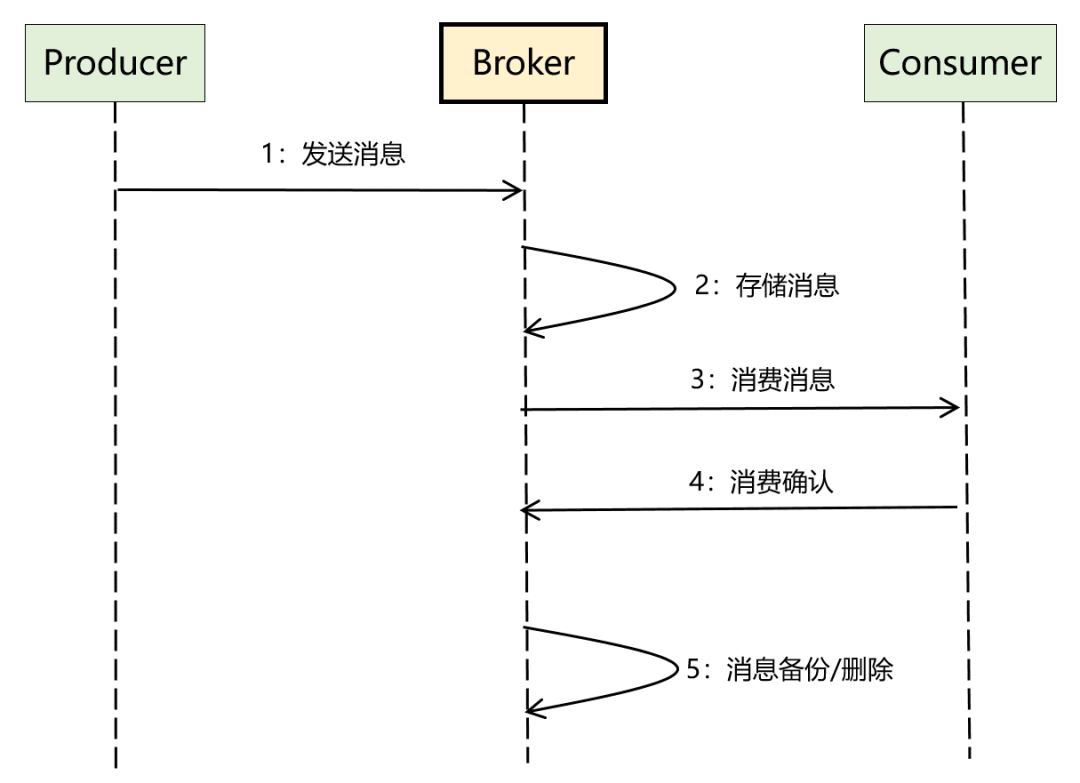
介绍：这篇文章对LSS方法中的瓶颈项进行分析，分别指出其中显存占用问题源自于“lift”操作生成的高维度特征，运行耗时是由于“splat”操作的求和操作，对此文章从矩阵变换的角度对原版的LSS方法进行改进，得到高效BEV特征生成方法MatrixVT。从FOV到BEV的变换是可被描述为一个矩阵变换的，但是直接去学习这样的矩阵变换是很难的，对此文中将以相机为原点的BEV特征进行正交分解得到：与相机的距离矩阵（对应文中的ring matrix）和与相机视线方向矩阵（对应文中的ray matrix），从而通过引入先验几何编码降低了整体学习的难度。此外，对图像深度信息在特征图$WH$两个维度的丰富程度进行分析，得出$W$这个维度包含的信息更多，则对应提出Prime Extraction Module消除$H$维度的特征，这样便可进一步降低计算量。文中给出文章的方法相比之前的LSS能快2～8倍，显存消耗减小97%。

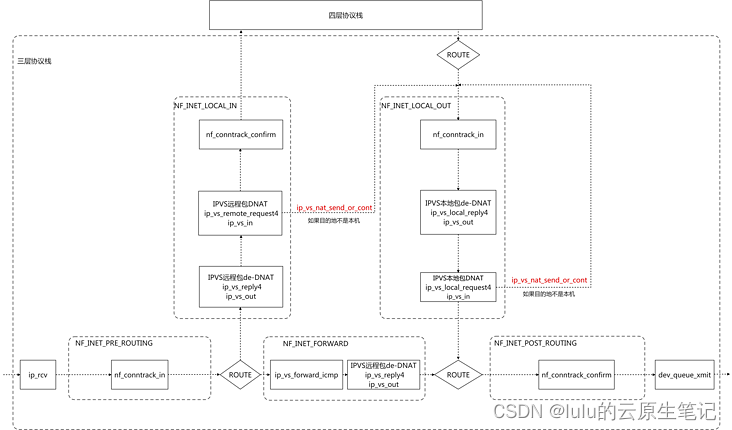
对于原本的LSS方法其流程可概括为下图所示：

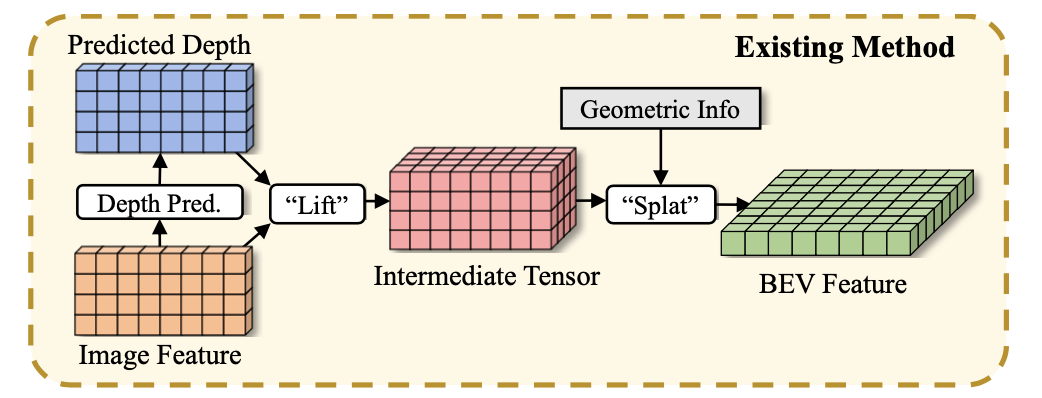
上图中“lift”和“splat”操作都是相当消耗资源的，对此首先是对图像特征在$H$维度进行压缩，之后通过ring matrix和ray matrix实现几何信息编码，同时通过计算等效转换还可进一步减少计算资源消耗，其结构见下图所示：

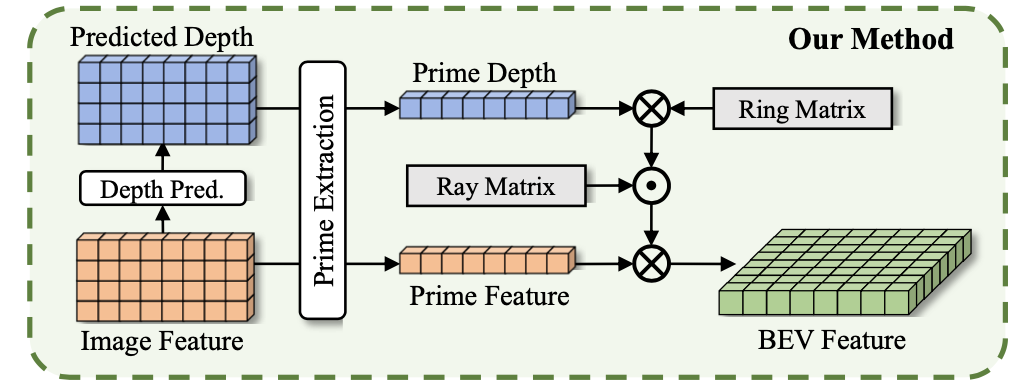
将这篇文章提到的方法与其它方法在耗时与显存消耗上的比较与分析：

2. 方法设计

2.1 方法pipeline

文章提出的BEV特征生成pipeline见下图所示：

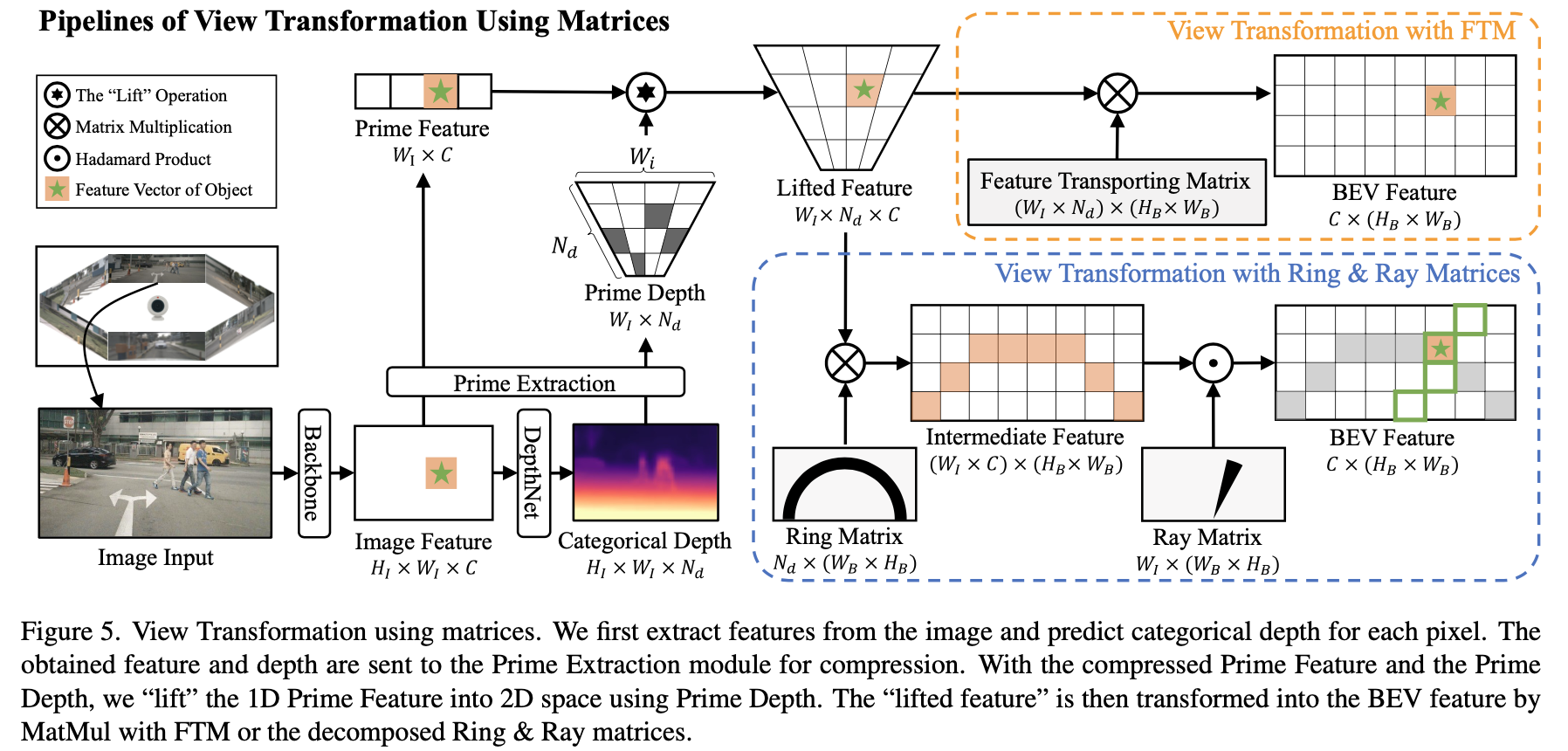
结合上图可将生成BEV特征的的流程划分为：

• 1）图像特征在$H$维度聚合（prime extraction module），源自与$W$维度比$H$维度有更丰富的特征表达，因此可将特征在$H$维度上聚合从而消减掉一个维度，从而减少计算开销。
• 2）$H$维度聚合之后图像上下文特征和深度特征（可有监督或是无监督）通过外积的形式组合起来，之后用矩阵变换的形式实现FOV到BEV的转换，这里转换矩阵显著使用了空间几何信息（构建了与距离和方向相关联的ring matrix和ray matrix）。

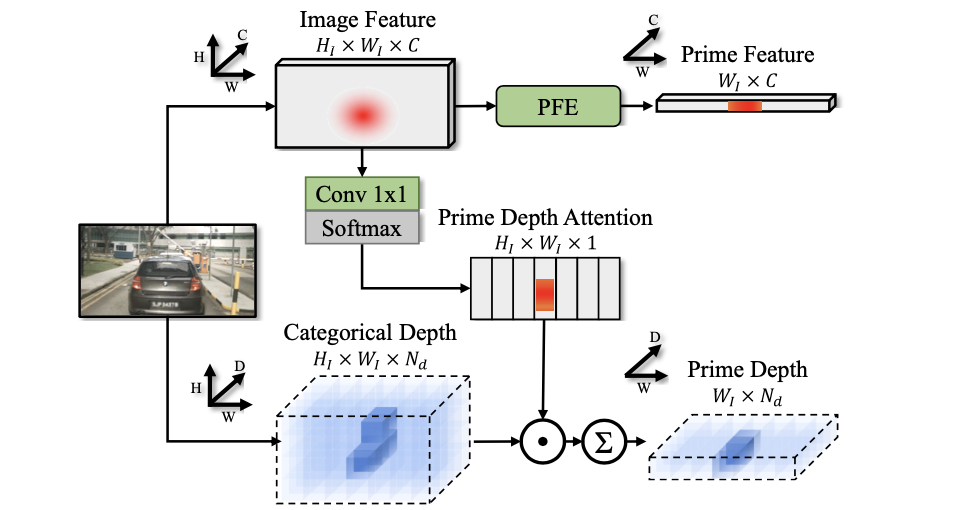
2.2 Prime Extraction Module

基于LSS的方法往往会生成两个特征：$F\in R^{N_c\ast H_I\ast W_I\ast C}$和$D\in R^{N_c\ast H_I\ast W_I\ast N_d}$，分别代表图像上下文和深度特征 。之后通过外积得到一个高维度的特征聚合$F_{inter}\in R^{N_c\ast H_I\ast W_I\ast D\ast C}$，这也就是“lift”操作。为了减少这一步过程中的显存消耗，这里对$H$维度特征进行消除，其观察源自于$H$维度的特征少于$W$维度，如下图：

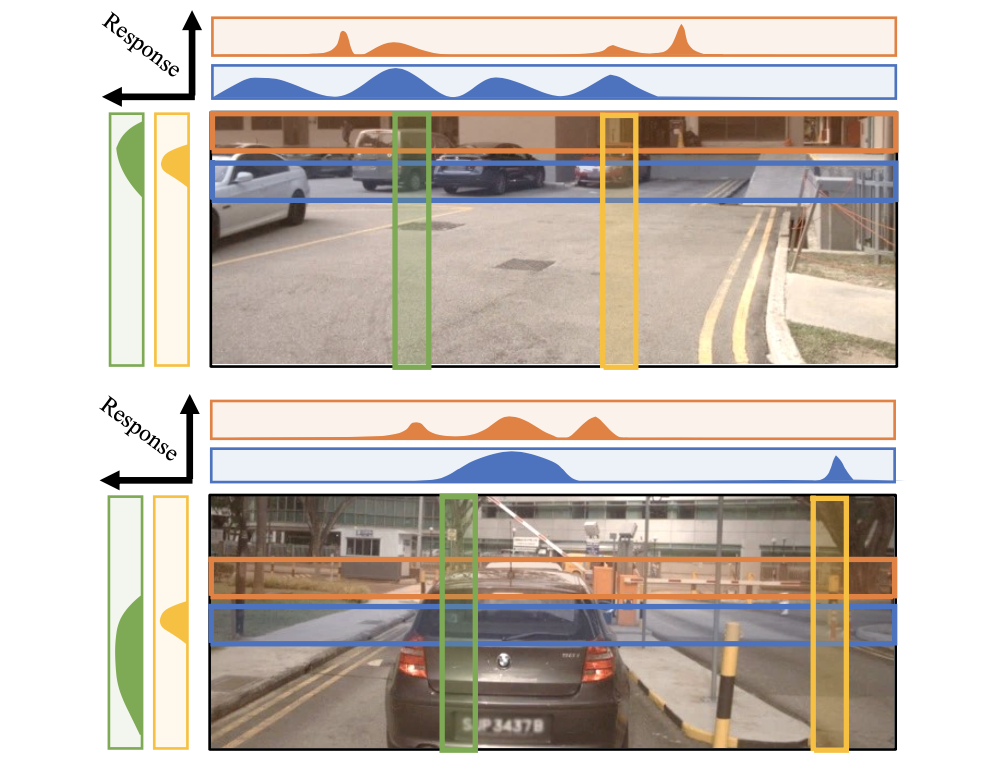
对此分别在图像和深度特征上对$H$维度进行压缩，其采用的结构见下图：

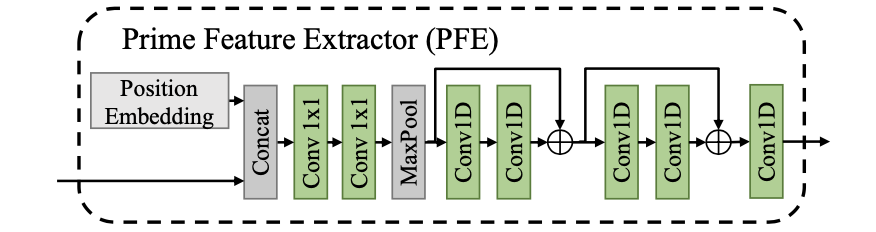
其中对于图像维度是通过maxpool来实现的：

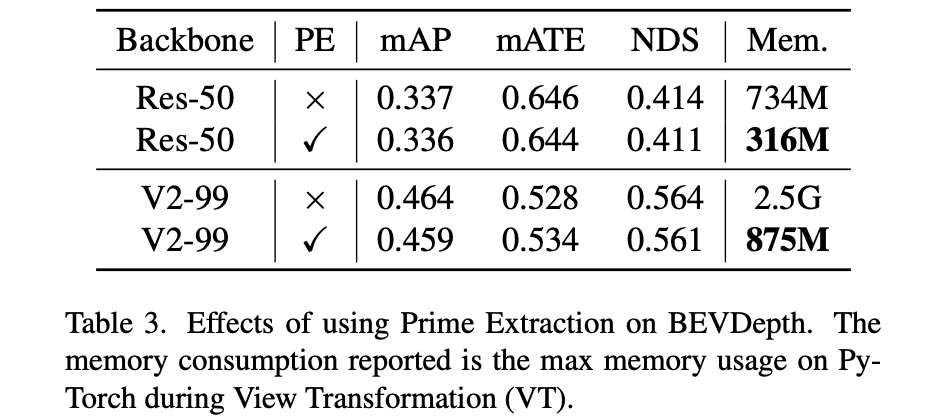
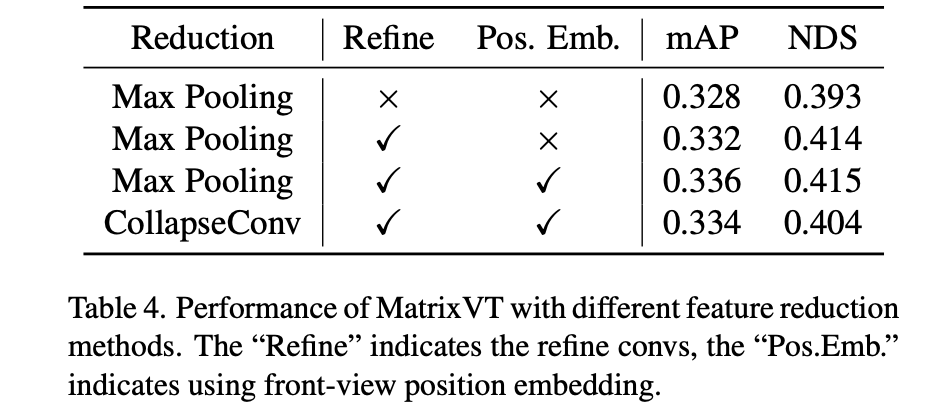
对于上述的过程其中的位置编码、maxpool等操作的消融实验见下表：

2.3 FOV到BEV的转换矩阵

在对$H$维度进行压缩之后得到得到包含深度和上下文的新特征$F_{inter}^w\in R^{N_c\ast W_I\ast N_d\ast C}$，那么要将其转换到BEV特征下则需要的转换矩阵为$M_{FT}\in R^{W_I\ast N_d\ast W_B\ast H_B}$，这步对应原版LSS方法中的“splat”操作。但是直接对上述的矩阵进行乘法操作，一是会增加学习的难度，而是计算量也会比较大。对此文章设计了ring matrix（$M_{ray}\in R^{W_I\ast (W_B\ast H_B)}$）和ray matrix（$M_{ray}\in R^{N_d\ast (W_B\ast H_B)}$），那么对应的变换矩阵就可通过分解计算量得到较大减少。则从FOV到BEV的特征转换可以被描述为：
$$F_{BEV}=\sum _w[M_{ray}\odot (M_{ring}\cdot F_{inter}^w){]}^{\ast w}$$
则将上述的变换关系与之前的“lift”过程联系起来，可以对其进行等价转换：
$$F_{BEV}=(M_{ray}\odot (M_{ring}\cdot D))\cdot F$$

3. 实验结果

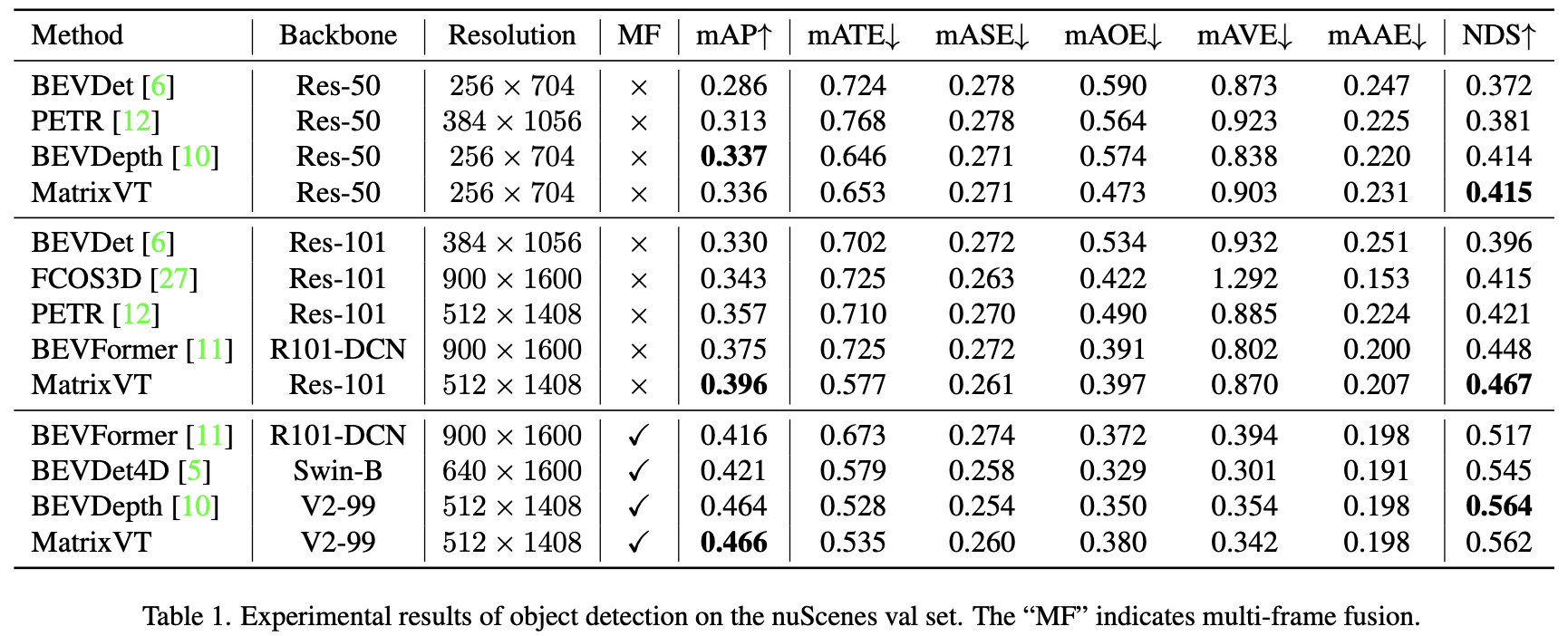
nuScenes val上的检测性能：

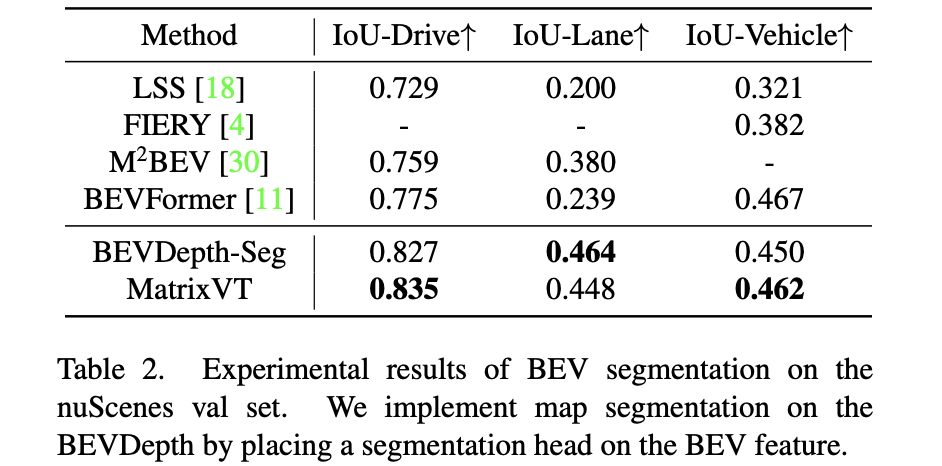
分割性能比较：

Prime Extraction模块对性能和显存消耗的影响：