1、深度学习了解

1.1 深度学习简介

机器学习：获取数据–特征提取–分类器–输出
深度学习：获取数据–深度学习 --输出
深度学习是机器学习的一个子集，不需要手工设计特征，可解释性差，效果好
应用场景：图像识别、语音识别、机器翻译、自动驾驶

历史：
1989年：反向传播算法
2012年：李飞飞imageNet首次使用深度学习
2019年：transformer

1.2 神经网络

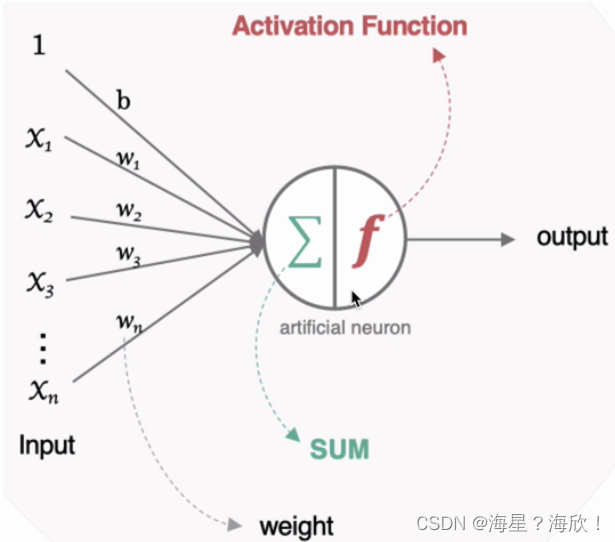
神经网络：人工神经网络，是一种模仿生物神经网络结构和功能的计算模型。
神经元之间传递复杂的电信号，树突接收到输入信号，然后对信号进行处理，通过轴突输出信号
神经网络：对每个神经元的输入进行加权和，送人激活函数后进行输出
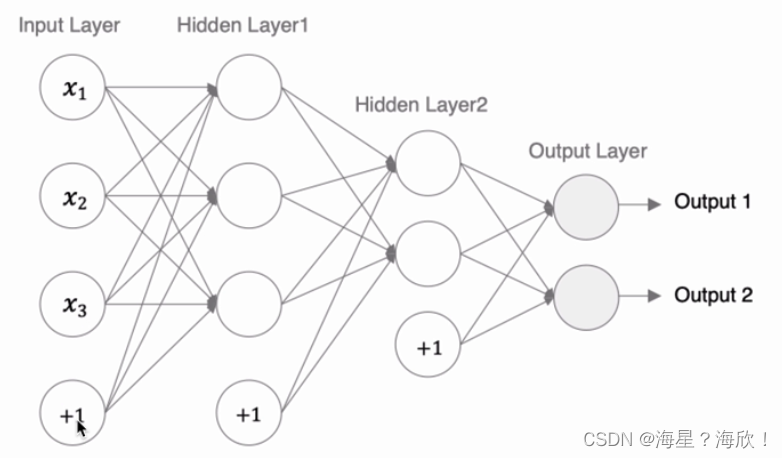
输入层：对应的输入数据
隐藏层：输入与输出之间的
输出层：获取输出的
特点：
1，每一层的神经元之间没有连接
2，当前层的输入是上一层神经元的输出
3，数据传输过程：输入->隐藏层->输出层

2、神经网络的工作流程

2.1 激活函数

激活函数作用：向神经网络中引入非线性因素
通过激活函数，神经网络可以拟合各种曲线。如果不用激活函数，每一层输出都是上一层输入的线性函数。

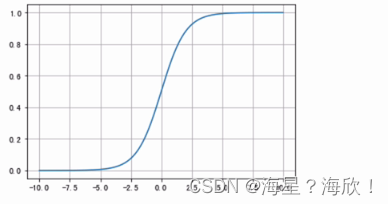
2.1.1 Sigmoid/Logistics函数

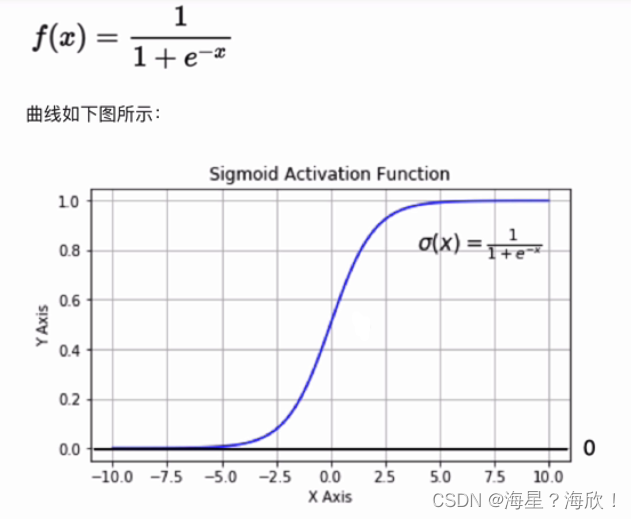
处处可导
在x足够小或者足够大的时候，导师为0，容易造成梯度消失
sigmoid一般只用于二分类的输出层

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-10,10,1000)
y = tf.nn.sigmoid(x)
plt.plot(x,y)
plt.grid()

2.1.2 tanh（双曲正切曲线）

上面的sigmiod曲线的中心点不在原地，所以出现了tanh

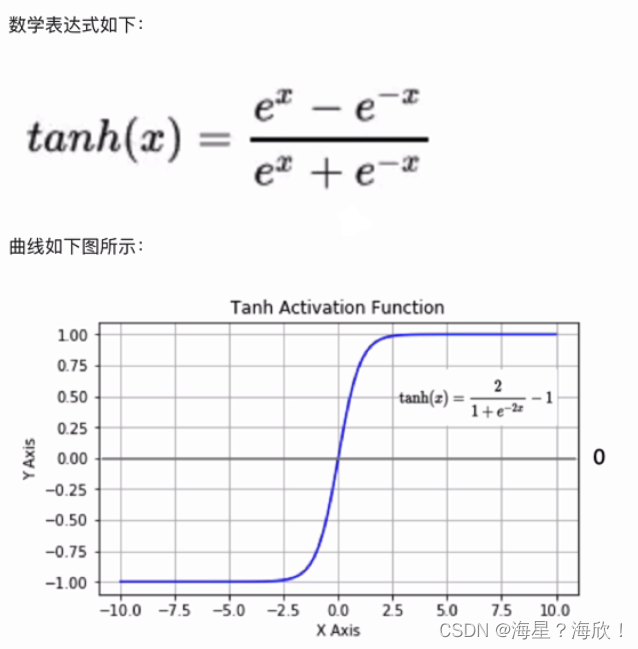
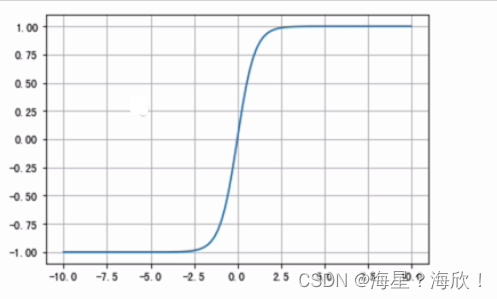
y范围：-1到1
tanh函数是以0为中心的，收敛速度比sigmoid快(更陡峭)，减少迭代次数，两侧的导数为0，同样会造成梯度消失。
使用时，可在隐藏层使用tanh函数，在输出层使用sigmoid函数

x = np.linspace(-10,10,100)
y = tf.nn.tanh(x)
plt.plot(x,y)
plt.grid()

2.1.3 RELU

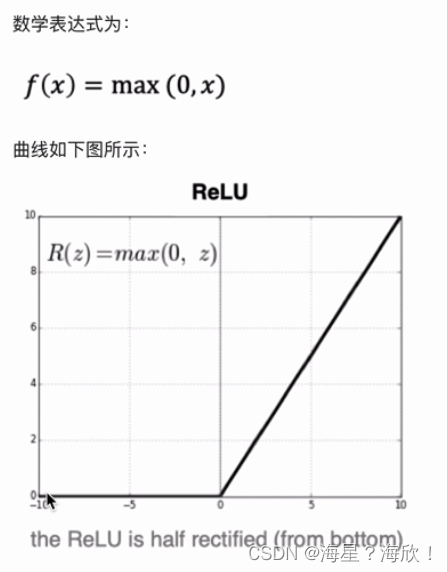
ReLU是目前最常用的激活函数，
在x<0时，ReLU导数为0，落入小于0区域时，权重无法更新，这种称为“神经元死亡”，缓解过拟合问题
在x>0时，是其本身，缓解梯度消失问题
与sigmoid相比，RELU的优势：
1，采用sigmoid函数时计算量大，而采用Relu时，计算量会节省很多
2，sigmiod容易出现梯度消失问题，从而无法完成深层网络的训练
3，Relu会使得一部分神经元的输出为0，造成网络的稀疏性，减少了参数的相互依存关系，缓解过拟合问题

x = linespace(-10,10,100)
y = tf.nn.relu(x)
plt.plot(x,y)
plt.grid()

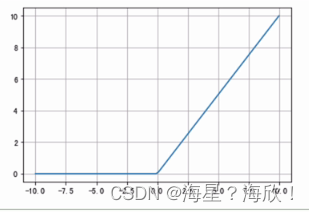
无脑使用relu

2.1.4 Leaky Relu

改进Leaky Relu
对于relu，防止出现大量神经元死亡问题，所以引入了leakrelu

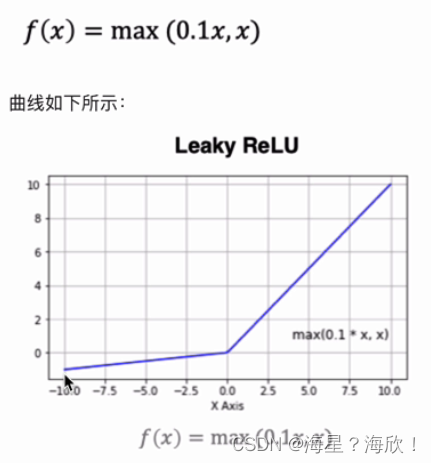
小于0时，导数是一个常数

x = linespace(-10,10,100)
y = tf.nn.leaky_relu(x)
plt.plot(x,y)
plt.grid()

2.1.5 SoftMax

SoftMax用于多分类过程中，它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结构以概率的形式展示出来

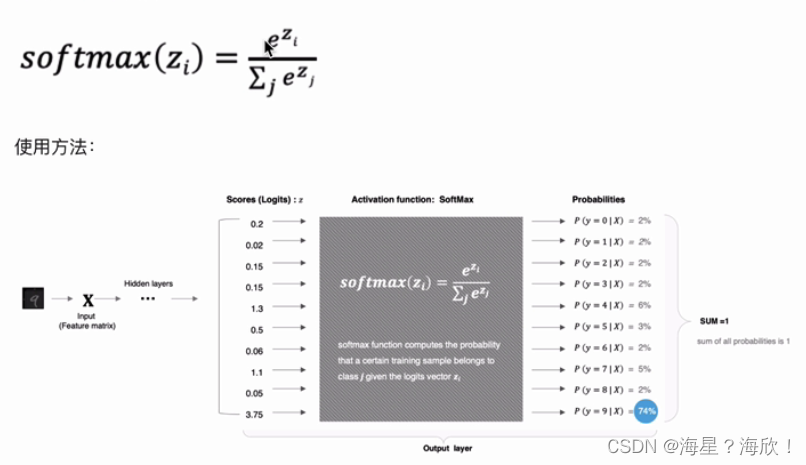
网络输出的logits通过softmax函数，就映射成（0，1）的值，理解为概率，选择概率最大的接点作为我们的预测目标类别

x = tf.constant([0.2,0.02,0.15,1.3,0.5,0.06,1.1,0.05,3.75])
y = tf.nn.softmax(x)

2.1.6 其他激活函数

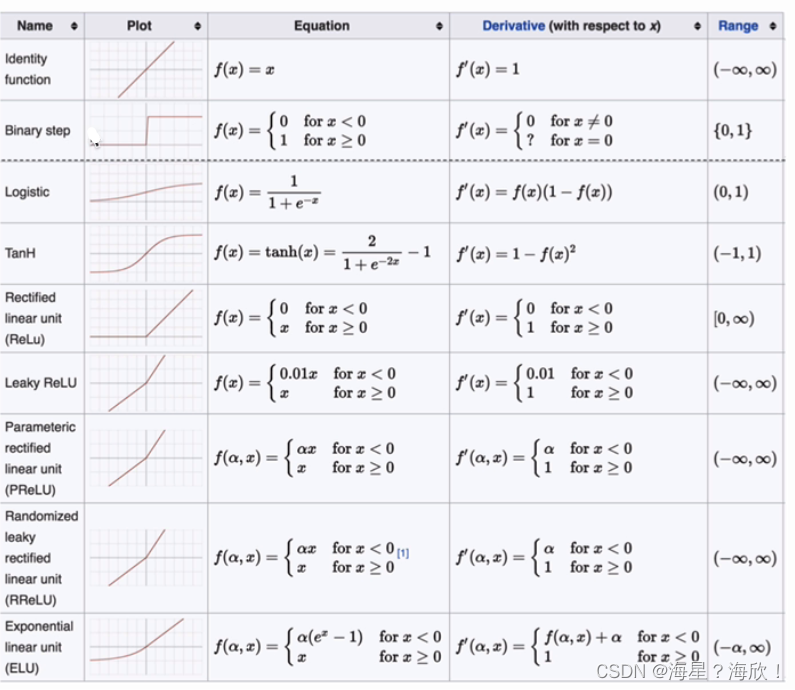
怎么选择激活函数？
隐藏层：优先relu，再leakyrelu，不要使用sigmoid，使用tanh
输出层：二分类–sigmoid ;多分类—softmax ; 回归—恒等激活

2.2 参数初始化

对于某一个神经元来说，需要初始化的参数有两类，一类权重W，还有一类偏置b，偏置b初始化为0即可，权重的初始化很重要

下面是对权重初始化的方法：

2.2.1 随机初始化

从均值为0，标准差为1的高斯分布中取样， 使用一些很小的值对w进行初始化

2.2.2 标准初始化

权重参数初始化从区间均匀分布随机取值，（-1/对d开根号，1/对d开根号)均匀分布中生成当前神经元的权重，其中d为每个神经元的输入数量

2.2.3 Xavier初始化

各层的激活值和梯度的方差在传播过程中保持一致，也叫做Glorot初始化。在tf.keras中实习方式有两种：
1，正态化Xavier初始化
从以0为中心，标准差为stddev = sqrt(2/(fan_in+fan_out))的正态分布中抽取样本，其中fan_in是输入神经元的个数，fan_out是输出的神经元个数

#正态化Xavier初始化
import tensorflow as tf
initializer = tf.keras.initializers.glorot_normal()
values = initializer((9,1)) #生成9行1列的权重
values

2，标准化Xavier初始化
从[-limit，limit]中的均匀分布中抽样采样，其中limit = sqrt(6/(fan_in+fan_out))，其中fan_in是输入神经元的个数，fan_out是输出的神经元个数

#标准化Xavier初始化
import tensorflow as tf
initializer = tf.keras.initializers.glorot_uniform()
values = initializer((9,1)) #生成9行1列的均匀分布的权重
values

2.2.4 He初始化

正向传播时，激活值的方差保持不变；反向传播时，关于状态值的梯度的方差保持不变。在tf.keras中也有两种：
1，正态化的he初始化
从以0为中心，标准差为stddev = sqrt(2/(fan_in))的正态分布中抽取样本，其中fan_in是输入神经元的个数

#正态化的he初始化
import tensorflow as tf
initializer = tf.keras.initializers.he_normal() #实例化
values = initializer((9,1)) #生成9行1列的权重
values

2，标准化Xavier初始化
从[-limit，limit]中的均匀分布中抽样采样，其中limit = sqrt(6/(fan_in)，其中fan_in是输入神经元的个数

#标准化Xavier初始化
import tensorflow as tf
initializer = tf.keras.initializers.he_uniform()
values = initializer((9,1)) #生成9行1列的均匀分布的权重
values

相较于Xavier，he初始化只考虑了输入神经元数

3，神经网络的搭建

tf.Keras中构建模有两种方式，一种通过Sequential构建，一种通过Model类构建。前者是按照一定的顺序对层进行堆叠，而后者可以构建较复杂的网络模型
构建网络层----tf.keras.layers.dense()

3.1 通过Sequential构建

Sequential（）提供了一个层的列表，能够快速构建一个神经网络模型
输入层–隐藏层–输出层

#Sequential构建神经网络
import tensorflow as tf
import tensorflow.keras as keras
import tensorflow.keras.layers as layers

model = keras.Sequential([
	#第一隐藏层
	layers.Dense(3,activation='relu',kernel_initializer = 'he_normal',name='layer1',input_shape=(3,)),
	#3个神经元，激活函数，初始化方式，当前层名字，3个输入
	#第二隐藏层
	layers.Dense(2,activation='relu',kernel_initializer = 'he_normal',name='layer2'),
	#输出层
	layers.Dense(2,activation='sigmoid',kernel_initializer = 'he_normal',name='layer3')
]
	name = 'sequential' #当前model的名字
)

model.summary()#展示模型结果
keras.utils.plot_model(model)

param指参数，权重的个数。43 =12；42=8；3*2=6

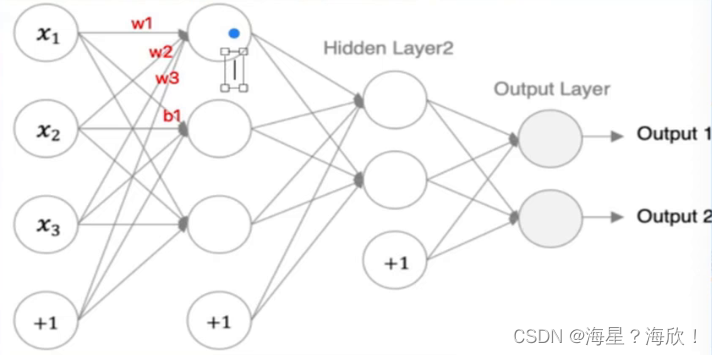
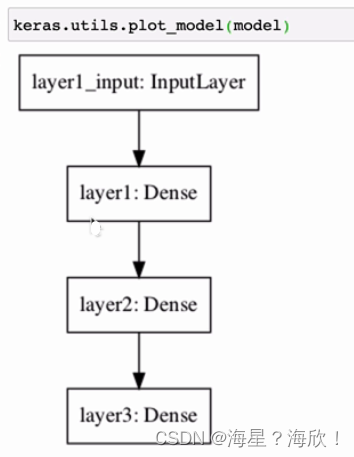
Sequentia只能构建简单的模型，单输入单输出类型的

3.2 通过function API构建–实践中常用

function API可以构建更为复杂的模型，将层作为可调用的对象并返回张量，并将输入向量和输出向量提供给tf.keras.Model的inputs和outputs参数

#function API构建神经网络
import tensorflow as tf
import tensorflow.keras as keras
import tensorflow.keras.layers as layers

inputs = keras.Input(shape=(3,),name=input) #定义输入：tf.keras.input
#第一隐藏层
x = layers.Dense(3,activation='relu',name='layer1')(input)  #要指定隐藏层的输入
#第二隐藏层
x = layers.Dense(2,activation='relu',name='layer1')(x)
#输出层
layers.Dense(2,activation='sigmoid',name='layer3')(x)
#创建模型
model = keras.Model(input=inputs,outputs = outputs,name='Function API Model')#构建模型tf.keras.Model

model.summary()#展示模型结果
keras.utils.plot_model(model,show_shapes=True)#绘制出模型结果

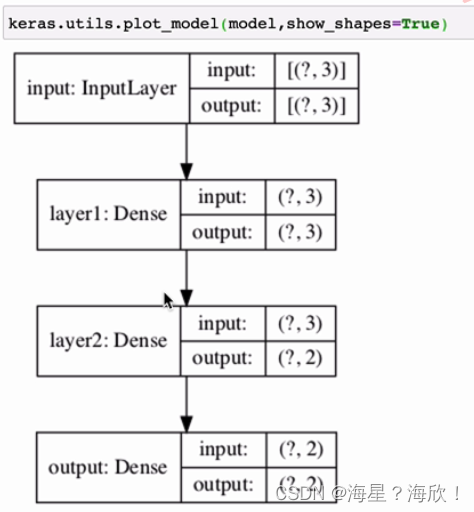
3.3 通过model的子类构建

通过model的子类构建模型，需要在__init__中定义神经网络的层，在call方法中定义网络的前向传播过程

#model构建神经网络
import tensorflow as tf
import tensorflow.keras as keras
import tensorflow.keras.layers as layers

class Mymodel(keras.Model):
	#定义网络的层结构
	def __init__(self):
		super(Mymodel,self).__init__()
		#第一隐藏层
		x = layers.Dense(3,activation='relu',name='layer1')
		#第二隐藏层
		x = layers.Dense(2,activation='relu',name='layer1')
		#输出层
		layers.Dense(2,activation='sigmoid',name='layer3')
	#定义网络的前向传播
	def call(self,inputs):
		x = self.layer1(inputs)
		x = self.layer2(x)
		outputs = self.layer3(x)
		return outputs

#实例化
model = Mymodel()
#设置输入
x = tf.ones((1,3))
y = model(x)
y
model.summary()	
#这种方式下不能使用plot_model了

步骤：
1，定义一个tf.keras.model的子类
2，init 完成网络中层的构建
3，call 完成前向传播

4，神经网络的优缺点

优点：

• 精度高，优于其他的机器学习方法
• 可以近似任意的非线性模型
• 随着计算机硬件的发展，近年受到热捧，有大量的框架和库可供使用

缺点：

• 黑箱，无法解释模型内部是如何工作的
• 训练时间长，需要大量计算力
• 网络结构复杂，需要调整超参数
• 小数据集上表现不佳，容易发生过拟合

神经网络 发展历史：
1969年–单层感知机
1986年–反向传播
受制于计算机的硬件
2012年–ImageNet比赛上大放异彩
2016年–AlphaGo

5，总结