核心
Adam: 一种基低阶矩的自适应估计的随机目标函数的一阶梯度优化算法,该方法实现简单**,计算效率高,内存需求很少**,对梯度的对角线重新缩放不变,并且非常适合于在数据或参数方面较大问题,该方法也适用于非平稳目标和具有非常有噪声的或稀疏梯度问题。
- 数据大\参数多\数据大且参数多
- 非平稳目标
- 噪声\稀疏梯度\噪声和稀疏梯度.
超参数具有直观的解释,通常不需要什么调整。
讨论了Adam和灵感来源的相关算法之间的一些联系,分析了算法理论的收敛性,并给出了收敛速度和在线凸优化框架下的regret bound。实验结果表明:Adam在实践效果良好,优于其他随机优化方法,最后讨论了,基于无限范数的Adam变形。
介绍
基于随机梯度优化在许多科学和工程领域具有核心的实践意义。这些领域中许多问题可以转换为一些标量参数化目标函数的优化。
需要对其参数进行最大化或最小化。如果该函数关于其参数是可微的,则梯度下降是一种相对有效的优化方法。因为,计算了所有参数的一阶偏导数与仅仅计算的函数的计算复杂度相同。通常,目标函数是随机的,例如:许多目标函数是由在不同的数据子样本上评估的子函数的和组成的;在这种情况下,通过采用梯度步骤可以使优化更有效率个别子函数,即随机梯度下降(SGD)或上升。SGD被证明是一种高效和有效的优化方法,在许多机器学习成功案例中,如深度学习的最新进展。除了数据子采样之外,目标还可能有其他噪声源,如退化正则化。对于所有这些有噪声目标,都需要有效的随机优化技术。本文的重点是研究具有高维参数空间的随机目标的优化。在这些情况下,高阶优化方法是不适合的,本文的讨论将仅限于一阶方法。
- 具有高维空间的随机目标的优化。
本文提出了一种方法,一种有效的只需要一阶梯度的随机优化方法。该方法从梯度的第一和第二矩的估计中**,计算不同参数的个体自适应学习率**。Adam是Adaptive moment estimation的缩写,也就是自适应矩的估计。
方法结合了最近两种流行的方法的优点:AdaGrad, 其适用于稀疏梯度,和RMSProp。其在在线和非平稳设置中很有效。Adam的一些优点是,参数更新的大小是不变的梯度。它的步长近似由步长超参数,其不需要一个平稳的目标,它与稀疏梯度,自然执行一种形式的步长退火((annealing)。
- Algorithm: 描述了该算法及参数更新规则的性质。
- Initialization bias correction: 解释了初始化偏差矫正技术。
- Convergence analysis: 描述了在线凸规划中亚当收敛性的理论分析。
- Realated work: Adam在各种模型和数据集上始终优于其他方法。
- Experimet:证明了Adam是一个通用的算法,可以扩展到大规模的高维的机器学习问题。

手写笔记,后续的电子记录:


Initialization bias correction
初始化偏差纠正
正如前部分所述,Adaml利用了初始化偏差矫正项,这部分主要推导二阶矩估计项,与一阶矩推导是完全相似的。因而略写。

在稀疏梯度的情况下,要想对二阶矩进行可靠的估计,需要通过选择一个小小的
β
2
β2
β2值来平均许多梯度,然而,正式这种小
β
2
β2
β2的情况,缺乏初始化偏差矫正将导致初始步骤大的多。
收敛性分析
利用前人中提出的在线学习框架分析,Adam收敛性,由于序列性质是未知的,使用Regret来评估算法,最后,可以证明Adam的平均Regret程度是收敛。
相关工作
与Adam有直接关系的优化算法为RMSProp和AdaGrad.其他的随机优化算法包括:vSGD、AdaDelta 以及,Natural Newton method from Roux & Fitzgibbon。所有这些都是通过一阶信息估计曲率估计信息来设置步长的,函数和优化器(SFO)是一种基于小批量的准牛顿方法,但(不像Adam)对数据集的小批量分区的数量有线性的内存要求,这在GPU等内存约束系统上通常是不可行的。与自然梯度下降(NGD)一样,Adam采用了适应数据几何形状的预调节器,因为平方梯度是费雪信息矩阵(the Fisher information matrix)对角线的近似;然而,Adam的预调节器(像AdaGrad的**)在适应上比普通的NGD更保守**,通过对角费雪信息矩阵近似的平方根。
RMSProp
一种与Adam密切相关的最优化方法是RMSProp。有时也会使用一个有动量的版本。带动量的RMSProp和Adam之间有一些重要的区别:带动量的RMSProp使用重新调整的梯度上的动量来生成参数更新,而Adam更新是直接使用梯度的第一和第二矩的运行平均值来估计的。RMSProp也缺乏偏差校正项;在β2值接近1(稀疏梯度的情况下需要)时,这一点最重要,因为在这种情况下,不纠正偏差会导致非常大的步长和发散。
AdaGrad
一种适用于稀疏梯度的算法是AdaGrad。请注意,当去除偏差修正项时**,Adam和AdaGrad之间的直接对应关系并不存在**;如果没有偏差校正**,就像在RMSProp中那样,一个无限小地接近于1的β2会导致无限大的偏差和无限大的参数更新**。
实验
为了实证评估所提出的方法,研究了不同的流行的机器学习模型,包括逻辑回归、多层全连接神经网络和深度卷积神经网络。使用大型模型和数据集,证明了Adam可以有效地解决实际的深度学习问题。在比较不同的优化算法时使用相同的参数初始化。超参数,如学习率和动量,在一个密集的网格上搜索,并使用最佳的超参数设置报告结果。
- 在一个密集的网格上搜索,并使用最佳的超参数设置报告结果。

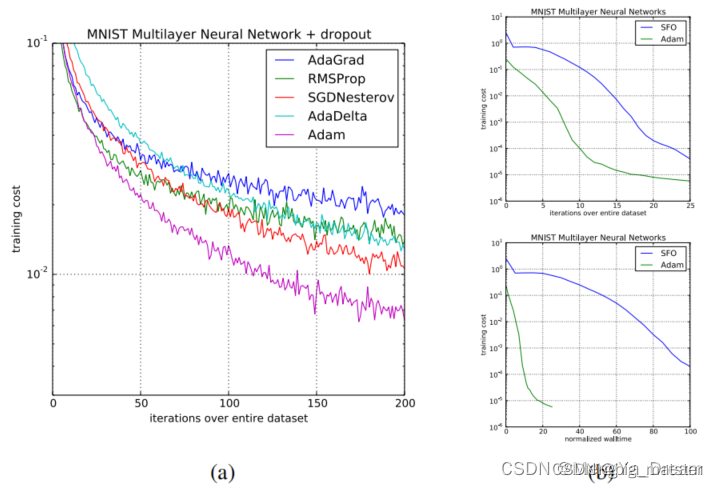
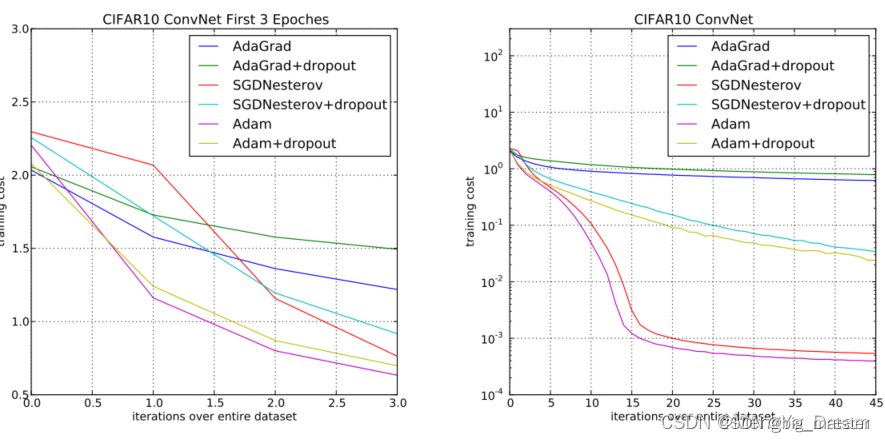
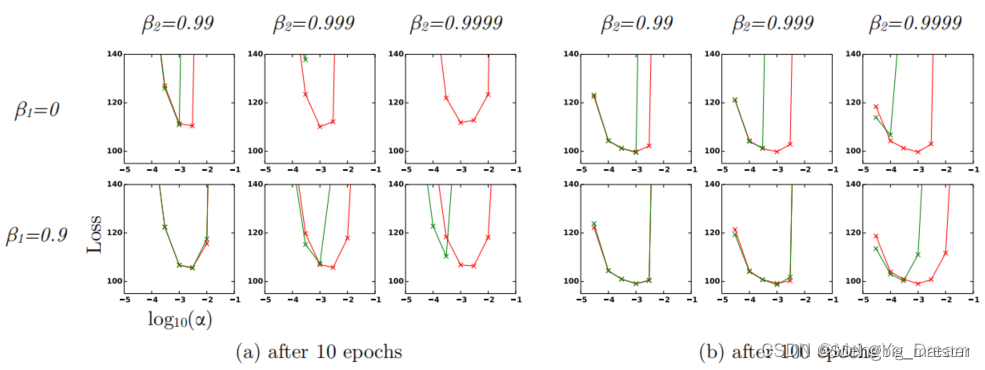
结论
介绍了一种简单且计算效率高的基于梯度的随机目标函数优化算法。旨在针对大型数据集和/或高维参数空间机器学习的问题。该方法结合了最近流行的两种优化方法的优点AdaGrad处理稀疏梯度的能力,和RMSProp处理非平稳目标的能力。该方法实现起来很简单,并且只需要很少的内存。实验证实了对凸问题的收敛速度的分析。总的来说,Adam**是鲁棒的,并且非常适合于领域机器学习中广泛的非凸优化问题**
- 大型数据集或高维度参数空间的机器学习。
- 非常适合于领域的机器学习中广泛的非凸优化问题。
创新点
- 根据梯度的第一和第二矩估计来计算不同参数的各个自适应学习率,(Adam自适应矩估计)。
- 结合两种流行方法的优点
- AdaGrad: 适用于稀疏梯度。
- RMSProp: 适用于线上和不平稳的设置.
主要贡献
- 实现简单,计算效率高,存储容量要求低,对梯度的对角重新缩放不变,并且非常适用于数据/参数方面的较大问题。
- 适用于目标不变和具有非常嘈杂/稀疏梯度的问题。
- 超参数具有直观的解释,并且通常只有很少的调整。
对该领域的认知
- 随机梯度优化在许多科学和工程领域具有重要的作用,这些领域中许多问题可以被视为一些标量目标函数优化,使其得到关于其参数的最大化和最小化。
- AdaGrad: 适用于稀疏梯度.
- RMSProp: 适用于在线和不平稳的情况。
经验
- 有时间会自己整理代码,将各种数学公式都了解一番,会自己推导。整个优化算法的数学公式,会自己了解即可。慢慢的都将其整理完整都行啦的理由与打算。
- 先着重发表文章,慢慢的会增加自己的数学知识,会自己将该领域的数学知识给其研究彻底,研究透彻。
- 慢慢的先将各种优化问题,全部都将其搞定。慢慢的将各种优化问题的数学公式全部都将其搞定,先根据这进行总结经验,会自己将各种数学公式,先自己会使用,然后再慢慢的再深入学习,懂里面的数学公式于基础,会深入理解各种数学问题,将其完全搞明白的都行啦的理由与打算。
- 会自己将其全部都搞定都行啦的理由与打算,会自己理解数学公式,将其全部都搞定都行啦的理由与打算。