一、LeetCode：199. 二叉树的右视图

LeetCode：199. 二叉树的右视图

差点因为是个中等题打退堂鼓。其实比较简单。
右视图实际上只需要找到，每一层的最右边的那个结点即可。
dfs：

• 确保每次找到底层最右边的结点，时间复杂度$O(n)$

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        cur_floor = 0;
        rightNode(root,0);
        return ans;
    }
private:
    void rightNode(TreeNode * root,int floor){//找到当前层最靠右的结点
        if(!root) return;
        if(floor == cur_floor){
            ans.emplace_back(root->val);
            cur_floor++;
        }
        rightNode(root->right,floor + 1);
        rightNode(root->left, floor + 1);
        return;
    }
    int cur_floor;
    vector<int> ans;
};

实际上使用层序遍历更好理解，每次选择一层的最后一个节点就行！

---

二、LeetCode：437. 路径总和 III

LeetCode：437. 路径总和 III

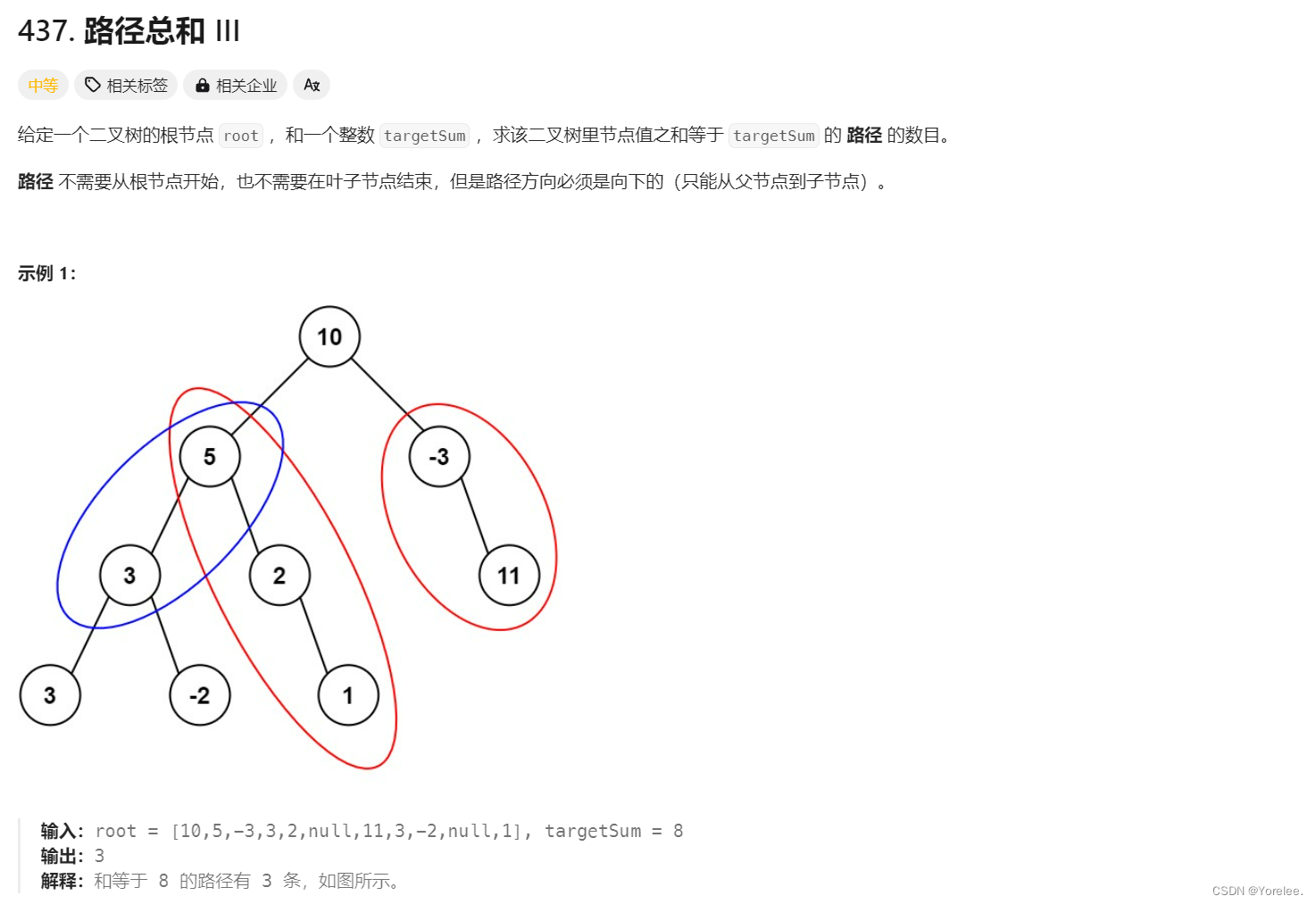
这个问题使用dfs可以解决，不过实现起来比较复杂，时间复杂度是$O(n^2)$。我们先考虑其他方法。

发现使用树上前缀和很容易解决，最坏时间复杂度也是$O(n^2)$，所以我们先考虑使用前缀和。
未优化的前缀和+dfs回溯：

• 最坏时间复杂度是$O(n^2)$
• 前缀和求和，需要考虑元素大小的问题，所以要使用long long！
• 对于每一个结点需要求其前缀和，以及以当前结点结尾的序列的值的总和是否存在等于targetSum的
• 向下递归左右子节点，向上回溯。

class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) {
        if(!root) return 0;
        vector<long long> presum;
        presum.emplace_back(0);//导入前导0
        getNum(root,targetSum,presum);
        return Num;
    }
private:
    void getNum(TreeNode * root,int targetSum,vector<long long> & presum){
        if(!root) return;
        //压入当前值的前缀和
        presum.emplace_back(root->val + presum.back());

        //判断以当前结点结尾的序列是否存在targetSum，由于存在负值，因此无法提前break
        for(int i = presum.size() - 2;i >= 0;--i){
            if(presum.back() - presum.at(i) == targetSum){
                ++Num;
            }
        }
        //继续向下递归
        getNum(root->left,targetSum,presum);
        getNum(root->right,targetSum,presum);
        //弹出当前值回溯
        presum.pop_back();
        return;
    }
    int Num=0;
};

---

做过两数之和之后很容易想到使用哈希表直接查找使用存在所需要的值。

• $presum1-presum2=targetSum$
• 则 $presum2=presum1-targetSum$

我们真的是需要哈希表找到需要的值吗？在这里我们只需要之前有多少个这样的值就行了！
因此哈希的key = 目标前缀和,value = 目标前缀和的个数

使用哈希优化的前缀和+dfs回溯：

• 哈希查找，每个结点查找一次，平均时间复杂度$O(1)$，整个时间复杂度为$O(n)$
• 使用std::unordered_map的count方法，返回值是0或1表示存在或不存在。
• 必须先判断是否存在所需前缀和，再压入当前值。 原因是当前值和所需前缀和可能刚好相等，导致当前前缀和也变成了答案的一部分，但实际上它不能是答案的一部分相当于之前所说的是同一个前缀和了，这使得序列为空。

class Solution {
public:
    int pathSum(TreeNode* root, int target) {
        if(!root) return 0;
        targetSum = target;
        presum_num[0] = 1;//导入前导0
        getNum(root,0);
        return Num;
    }
private:
    void getNum(TreeNode * root,long long presum){
        if(!root) return;
        long long cur_presum = presum + root->val;

        //判断以当前结点结尾的序列是否存在targetSum
        if(presum_num.count(cur_presum - targetSum) != 0)
            Num += presum_num[cur_presum - targetSum];
        
        //压入当前值的前缀和
        presum_num[cur_presum]++;

        //继续向下递归
        getNum(root->left,cur_presum);
        getNum(root->right,cur_presum);
        //弹出当前值回溯
        if(presum_num[cur_presum] != 1) presum_num[cur_presum]--;
        else presum_num.erase(cur_presum);
        return;
    }
    int Num=0;
    int targetSum;
    unordered_map<long long,int> presum_num;
};

---

前缀和的方法如果之前接触过很容易想到，不过这里建议学习深度优先遍历的方法，更深入理解dfs。
dfs：

• 时间复杂度：$O(n^2)$
• 实现两个递归函数：
  • 第一个函数dfs：以根结点开始向下求和，得到targetSum则Num++
  • 第二个函数getNum：遍历所有树节点，每个结点调用dfs函数。

class Solution {
public:
    int pathSum(TreeNode* root, int target) {
        targetSum = target;
        getNum(root);
        return Num;
    }
private:
    void getNum(TreeNode * root){
        if(!root) return;
        dfs(root,0);//包含本结点向下递归
        getNum(root->left);
        getNum(root->right);
        return;
    }
    void dfs(TreeNode * root,long long sum){
        if(!root) return;
        if(root->val + sum == targetSum) Num++;
        dfs(root->left,sum + root->val);
        dfs(root->right,sum + root->val);
        return;
    }
    int Num = 0;
    int targetSum;
};