题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

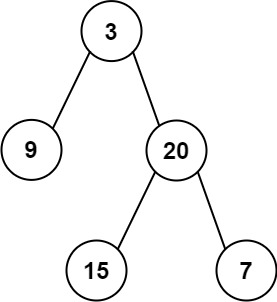
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

---

面试中遇到过这道题?

1/5

是

否

通过次数

643.7K

提交次数

899.1K

通过率

71.6%

结点结构

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

方法

先在中序遍历中找到根的位置，然后用根来分隔左子树右子树在前、中序遍历的范围，然后递归建树。

代码

class Solution {
public:
    TreeNode* trackback(int l1,int r1,int l2,int r2,vector<int>& preorder,vector<int>& inorder)
    {
        //参数依次为前序遍历的左、右端点，中序遍历的左、右端点
        if(l1>r1) return NULL;
        //找根节点在中序遍历的位置
        int mid=l2;
        while(mid<=r2&&inorder[mid]!=preorder[l1])
            mid++;
        //构建根节点
        TreeNode *root=new TreeNode;
        root->val=preorder[l1];
        //递归构建右子树
        int L1,R1,L2,R2;
        L1=l1+1;
        R1=l1+mid-l2;
        L2=l2;
        R2=mid-1;
        //cout<<"("<<L1<<","<<R1<<","<<L2<<","<<R2<<")\n";
        root->left=trackback(L1,R1,L2,R2,preorder,inorder);
        //递归构建右子树
        L1=R1+1;
        R1=r1;
        L2=mid+1;
        R2=r2;
        //cout<<"("<<L1<<","<<R1<<","<<L2<<","<<R2<<")\n";
        root->right=trackback(L1,R1,L2,R2,preorder,inorder);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n=preorder.size();
        TreeNode *root=trackback(0,n-1,0,n-1,preorder,inorder);
        return root;
    }
};