欢迎来到博主的专栏——从0开始linux
博主ID:代码小豪
博主使用的linux发行版是:CentOS 7.6
不同版本下的操作可能存在差异
文章目录
- 命令
- 文件操作命令
- 文件树和文件路径
- 文件树
- 绝对路径
- 相对路径
- 文件属性
- tree指令
- 删除文件
- 复制文件
大家还记得在小学第一次上微机课的时候吗?老师在教学生使用windows系统的第一步通常都是创建文件夹。熟悉weindows系统的文件管理。那么想要了解linux,也可以从这一步开始。
命令
命令就是用户输入linux将执行的操作的指令,比如在windows系统当中,用户想要进入某个文件夹,那么就双击这个文件夹完成操作。
所有的命令的格式基本可以遵从下面的规则:
command [-options] 参数
(1)command是命令的名称,例如cd是转换工作目录。
(2)[~]当中的内容是选项,如果想要加入这个选项,需要在开头加上一个‘-’字符,比如-s。(并非所有命令都如此,只是这篇博客当中的命令都符合这个特性)
(3)并非所有的命令都有参数的。
(4)命令,选项、参数之间要有空格隔开,无论使用几个空格,都会视为1格、
(5)按下回车键,该命令开始执行。
(6)命令是区分大小写的,比如cd是命令,而CD不是
先来实操一下,比使用命令列出当前工作目录下的所有文件和文件信息。
ls -a -l#选项可以多选
ls -la#选项可以复用
ls -al#选项的顺序不重要
ls -al#中间的空格可以很多,只视为一个
选项是可以复用的,比如ls命令,其选项-a是列出所有文件,-l是列出文件信息(并非所有,隐藏文件不显示)。两个选项可以结合在一起,使用-al或者-la。
文件操作命令
(由于博客没有更新到用户这一概念,因此操作都是使用管理员root的权限下操作的,目的是为了让学习者快速使用命令进行文件操作,不过建议大家在使用linux的时候尽量用普通用户登录,除非要使用root权限)
mkdir [directoryname]
创建一个目录。在linux当中文件分为3中类型,分别是目录、普通文件和链接文件。linux当中的目录可以理解为windows当中的文件夹,其作用主要是进行文件的分类。
我们试着创建一个目录dir1,在命令行中输入
mkdir dir1
此时linux会在当前工作路径中生成一个dir1目录。由于我们没有图形用户界面,所以看不到当前工作路径存在什么文件
ls
ls是list file的缩写。其作用是列出当前工作目录下的文件。我们在命令行中输入ls,就可以看到创建的dir1目录了。
文件树和文件路径
windows系统的使用者应该对文件路径非常熟悉吧。用户在磁盘上寻找文件时,经过的文件夹的路线就叫做路径。
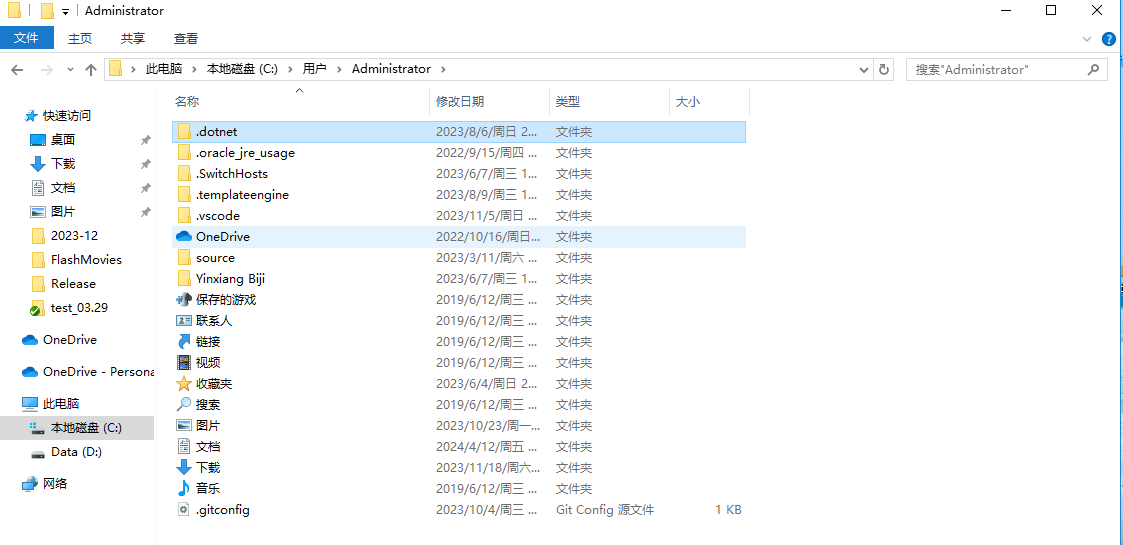
如上图,当前的工作文件的路径为:C:\Users\Administrator
那么在linux当中,我们可以使用pwd来显示当前工作路径
pwd

我们当前所处的路径为/root。这个root目录就是管理员root的家目录。linux的家目录就是每个用户登录时,最先进入的目录,这个目录存放用户的数据和文件。(类似于windows系统的c\Users<用户名>)
我们在这个家目录当中进入刚刚创建目录dir1。
cd <filename>
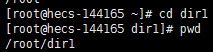
通过pwd命令,可以发现我们当前工作路径为/root/dir1。在路径中,目录之间会有一个\隔开。这个\称为路径分隔符。但是最开头的/却是一个例外,它不是一个符号,而是一个目录,称为根目录。在linux系统当中,所有的文件都是存在于根目录下的。不信的同学可以输入命令"cd /"进入根目录。
文件树
学习过数据结构的同学应该不会对“根”感到陌生,在linux系统下,所有的目录和文件都是从根目录开始的。那是所有文件的根节点。然后在根据目录一个个的分支下来,这就是一个多叉树的数据结构。因此,我们也称这种文件配置方式为:文件树。
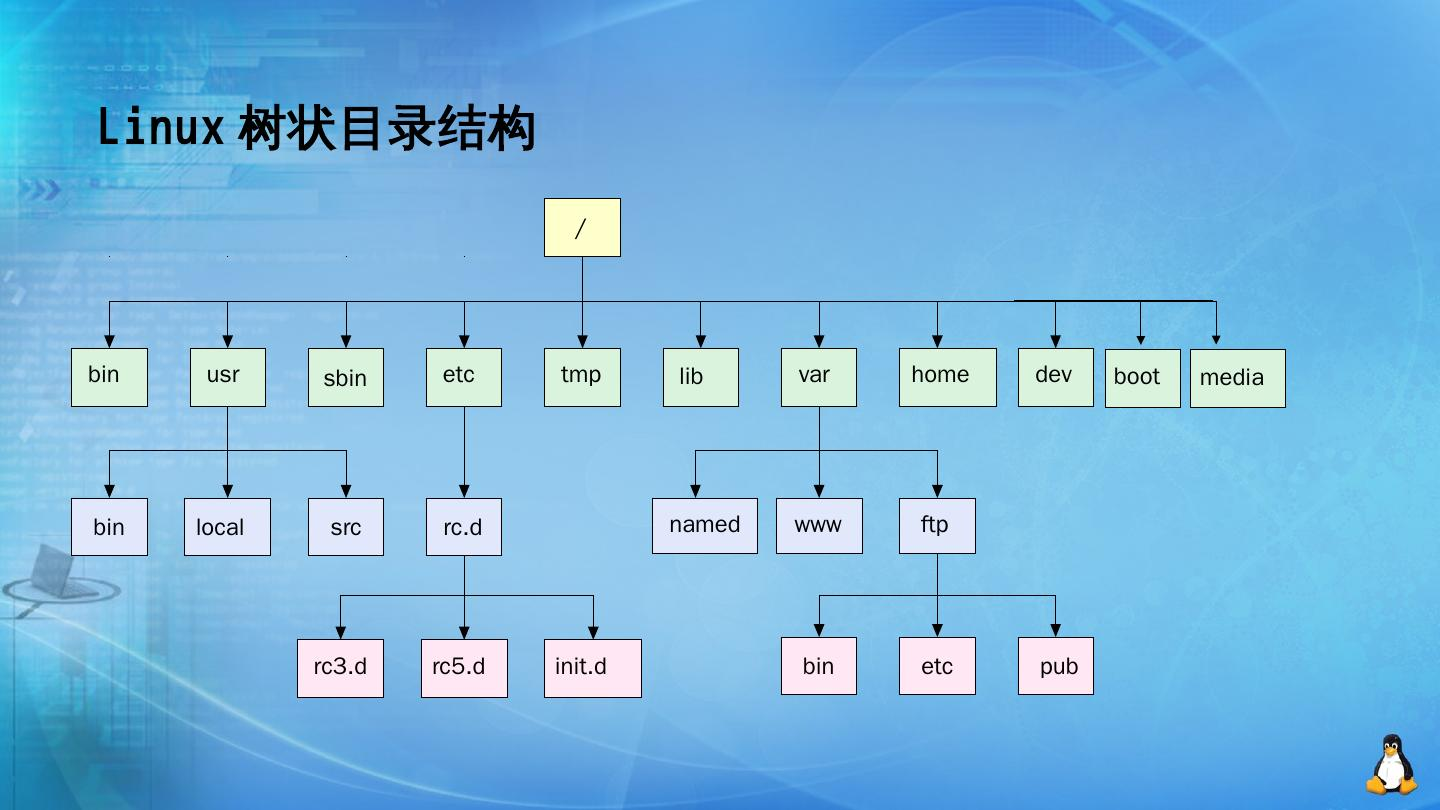
(网上找的qwq)。
linux的文件结构是一个多叉树,文件树有以下规律:
(1)空目录和普通文件是树的叶子结点
( 2)父节点可以有很多子节点,但是子节点只有一个父节点
(3)从根目录到任意文件的路径是唯一的
绝对路径
在文件树这个数据结构当中,每一个文件或者目录都是这个树的节点,出根目录外,其余节点都只存在一个父节点,因此从根目录开始,到文件树中任意文件,都有且只有一个路线,因此将这种从根目录开始到指定文件的路径,称为绝对路径
。
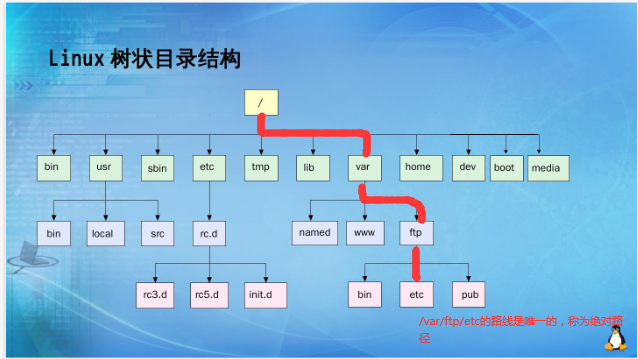
相对路径
我们在空目录dir1当中展示所有的文件。
ls -a

可以看到,即使是新建的空目录dir1当中,也存在两个特殊文件,一个是‘.’一个是’..'。
'.‘代表当前目录,也可以用’./'表示
‘..’代表上一级目录,也可以‘../’来表示。
比如现在想要回到上一级目录root,我们使用cd ../,创建一个dir2且进入dir2。
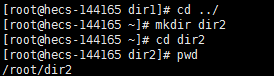
我们当前身处dir2目录当中,绝对路径是/root/dir2。如果我们想要进入dir1目录该怎么办呢?首先,我们回到上一级目录root当中,那么指令为cd ../。现在回到了root目录,接下来就是进入dir1目录,输入指令cd dir1。
这样做是不是太麻烦了,我们就结合起来一起写
cd ../dir1
这个../dir1就是dir1与dir2之间的相对路径。
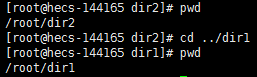
相对路径:相对于目前文件的文件名写法,例如dir1相对于dir2的相对路径为../dir1。只要开头不是根目录/的路径,就是相对路径。
如果要写相对路径是不是很麻烦啊,我们要熟悉整个linux的文件结构,这个肯定是非常难以做到的。所以我们可以先看看上级目录或者上上级目录存在什么文件,再去编写相对路径。
ls ../#查看上级目录
ls ../../#查看上上级目录

文件属性
ls -al可以查看当前目录下的所有文件信息。这里博主使用某个目录举例

拿empty文件为例

我们可以看到empty文件前面有各种各样的字符信息,这些字符信息就是文件属性。我们先来了解一下这些字段分别显示什么意思。
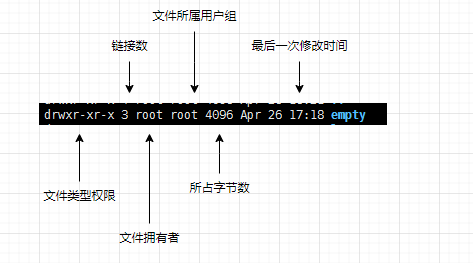
关于用户和用户组博主会专门开一个博客讲解,这里先卖个关子。
我们先开看第一个字段,即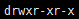
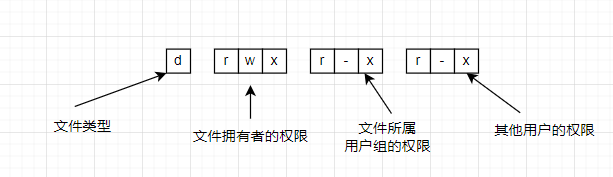
这个代表了这个文件的类型和权限。这个字段有十个字符组成。每一个字符都代表着不同的权限。
(1)第一个字符代表文件类型。比如[d]为目录文件,[-]为普通文件,[l]为链接文件等。
(2)剩余字符,每三个为一组,均为[rwx]三个参数的组合,其中[r]代表可读,[w]代表可写,[x]代表可执行。假如这个文件不具备可读权限,那么就会显示[-]。
(3)第一组表示的是文件拥有者的权限,如empty文件,文件拥有者root拥有可读可写可执行三个权限。
(4)第二组表示处于root用户组的成员的权限,只有可读和可执行的权限。
(5)第三组表示其他账号的权限。(非拥有者,也非用户组的账号)。也只有可读和可执行
tree指令
tree指令是需要下载的,我们在linux当中输入:
yum install -y tree
即可完成下载和安装
前面提到了,linux的文件结构是一个多叉树,tree指令可以以多叉树的结构显示目录下的全部文件。
常用方法分为以下几种
(1)用绝对路径显示该路径下的全部文件。
tree [绝对路径]
比如:
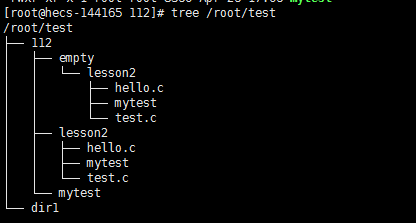
显示root目录下的test目录的所有文件。
(2)用相对路径显示该路径的全部文件。
tree [相对路径]
比如显示当前目录下的全部文件,我们可以用‘.’来展示当前路径下的所有文件。
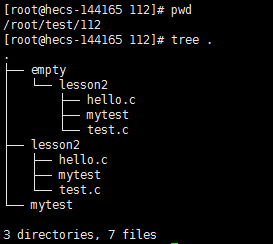
使用tree指令可以让我们快速了解某个目录下的文件结构,非常好用。
删除文件
rmdir:删除一个空目录
前面我们不是新建了一个空目录dir1吗?现在我们来试着删除一下dir1吧。
首先来到dir1的目录下。(如果你是跟着博主操作的,那么它应该在root目录下)
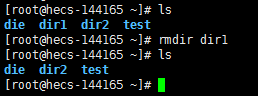
但是这个指令只能删除空目录,如果删除的目录中存在其他文件,那么这个指令则无法生效。比如博主的test文件是存在其他文件的。
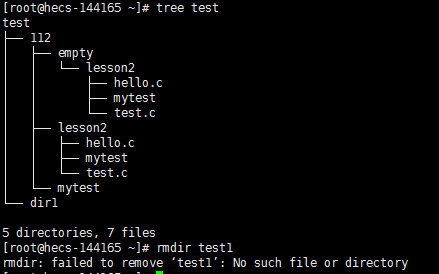
如果想要删除有文件的目录或者普通文件,我们需要用到rm指令,rm指令存在以下常用选项
rm [file]
选项:
-f----直接删除文件,不需要询问
-r----递归删除文件(删除指定目录下的所有文件)
如果我们使用不带选项的rm指令,那么它只能删除空目录和普通文件,比如我们创建一个文本文件。

当你删除文件时,linux会询问你是否删除这个文件,输入y选择是,输入n则取消这个操作。
所以rm -f可以让l操作系统不再询问你。
现在我们在root目录下创建一个目录dir1,然后再目录当中再创建一个目录dir2。由于此时dir1不再是空目录,因此我们不能用rm [filename]来删除dir1.
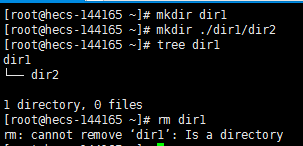
此时我们就需要用到rm -r命令。
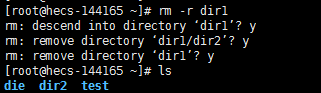
每删除一个文件,linux系统就询问你一次,这是非常麻烦啊。所以我们可以结合‘-f’和‘-r’指令,直接删除掉这个目录和该目录的其他文件。
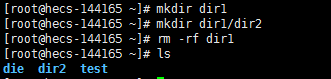
根目录是不是也是一个目录啊,所以这里我们就学到linux当中最经典的指令。
rm -rf /#将系统当中的所有文件都删除
这个指令也是最出名的删库跑路指令(出了事别说是小豪教的哈哈)。
如果你使用的时自己租的云服务器,那么你可以尝试,因为我们可以在云服务器的官网上重装系统,所以问题不大,但是使用虚拟机或者个人pc安装linux操作系统的同学们就慎用了。
这个指令只有root才有这个权限,普通用户是没有的(不然就乱套了),所以大家学习linux的时候尽量使用普通用户进行操作。
复制文件
复制文件我们通常用到cp命令。
cp的用法非常多,这里讲讲最常见的几种选项
cp [option] src(源文件) dest(目标文件)
-i—若目标文件已存在,在覆盖时会询问是否进行覆盖
-r—递归复制,将源文件的所有文件复制到目标文件当中
-f—不询问操作
由于没讲解文件的连接属性和修改文件属性的操作,因此只说明这三个选项
比如将test文件复制到root目录下,并命名为test2.
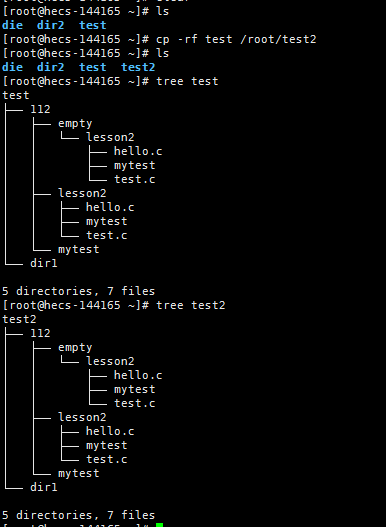
不难发现,test中的内容全都复制到了test2当中。
到这里我们已经学会了简单的文件操作了,趁命令还记在脑子里。快打开自己的linux系统开始练练手吧。