前言：该题主要是考对fontTools.ttLib.TTFont的操作，另外就是对字典互相映射的操作
一、woff文件存储
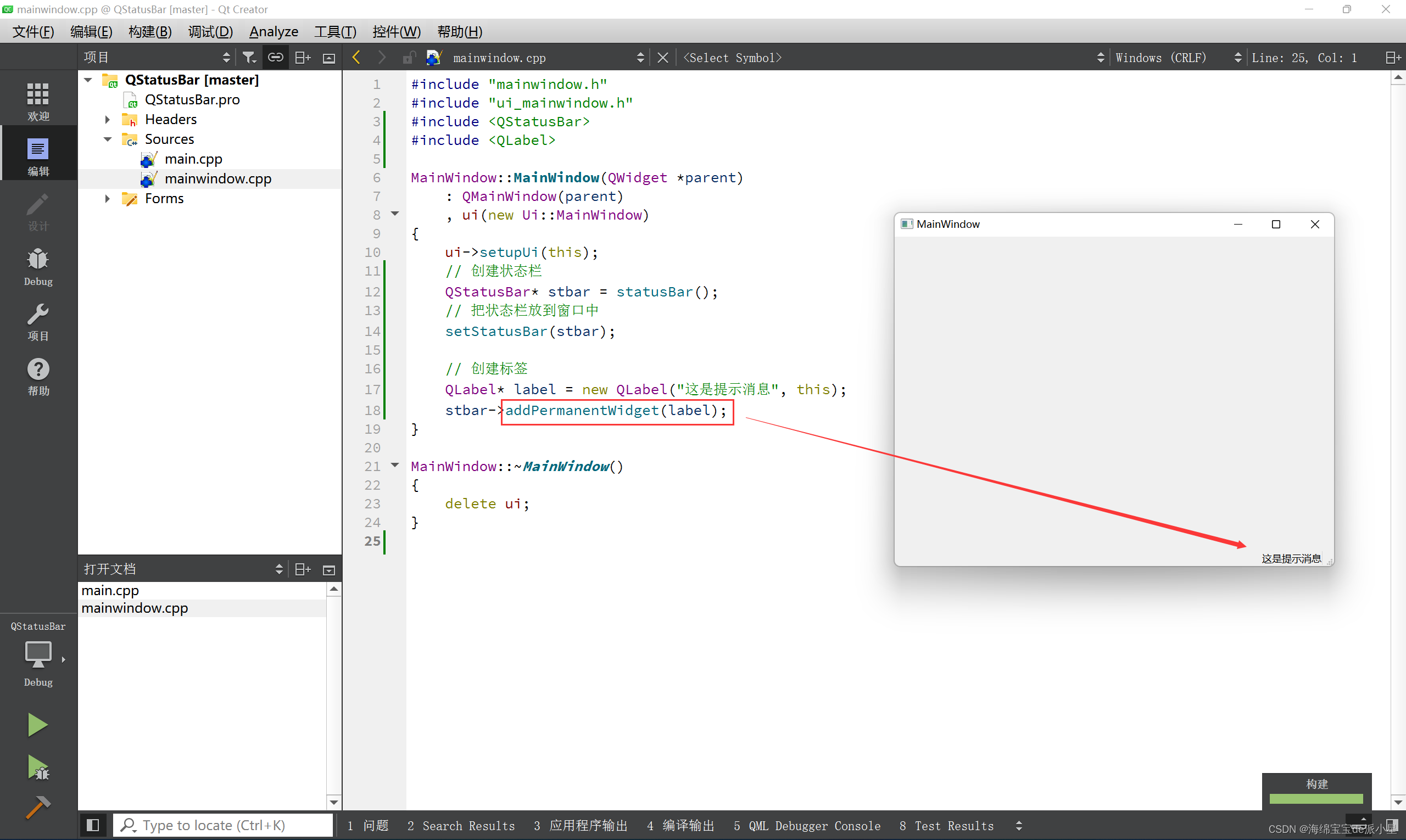
from fontTools.ttLib import TTFont #pip install fontTools
def save_woff(response):
woff = response['woff']
woff_file = base64.b64decode(woff.encode())
with open('aim.woff', 'wb') as f:
f.write(woff_file)二、可视化woff文件
1.首先要把woff文件存成xml格式
from fontTools.ttLib import TTFont
# 加载字体文件：
font = TTFont('ami.woff')
# 保存为xml文件：
font.saveXML('local_fonts.xml')2.利用网站查看
Iconfont Previewiconfont preview for web, Momo's Blog, LuckyMomo
https://blog.luckly-mjw.cn/tool-show/iconfont-preview/index.html
通过这两步可以建立初始化的name与num列表
三、抓取一页建立woff中flag与数字之间的关系
1.利用可视化网站手动输出woff中name与数字的关系
r_map = {'unic543': 0, 'unib928': 1, 'unic193': 2, 'unib958': 3, 'unia257': 4, 'unic829': 5, 'unib716': 6, 'unic182': 7,
'unic387': 8, 'unib718': 9} # 数字映射字典2.输出name与flag的关系
def base_font_map(woff):
"""构造基本on数组映射模板"""
ttobj = TTFont(woff)
tt_names = ttobj.getGlyphNames()[1:] # 获取所有name值
cmap = {}
for i in tt_names:
cmap[tuple(ttobj['glyf'][i].flags)] = i # 构造基本映射on数组模板
return cmap
print(base_font_map('aim.woff'))3.建立flag（on）与数字的关系
def on_num(on_name,name_num):
onnum={}
for key,value in on_name.items():
onnum[key]=name_num[value]
return onnum四、处理一页response.data数据
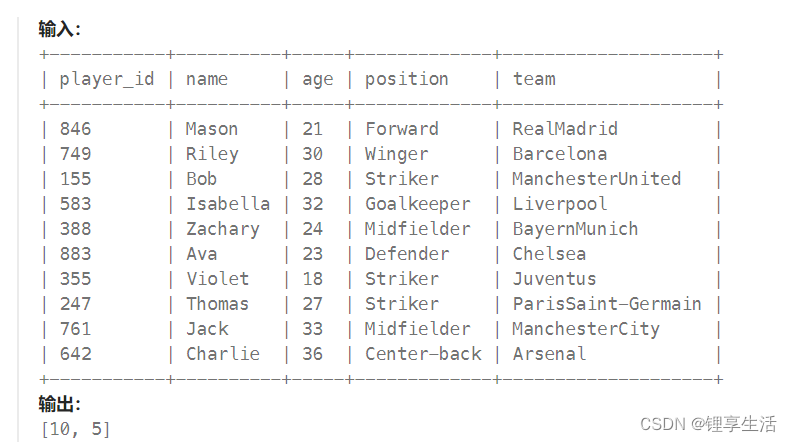
def page_data(data,page_name_num): #data=每一页解析的data数据，page_name_num=每一页解析出的name与num的对应关系
nums=[]
for d_v in data:
name_list=d_v['value'].replace('&#x','uni').split(' ')
if name_list[-1]=='':
name_list.pop()
point=''
for name in name_list:
point+=str(page_name_num[name])
nums.append(point)
return nums五、处理一页woff值中name与num的对应关系
def name_num(onnum,nameon):
namenum={}
for key,value in nameon.items():
namenum[key]=onnum[value]
return namenum
六、返回一页的point点
def page_point(page):
url = f"https://match.yuanrenxue.cn/api/match/7?page={page}"
response = requests.get(url, headers=headers, cookies=cookies).json()
data = response['data']
woff = response['woff']
save_woff(woff, page)
nameon = base_font_map(f'{page}.woff')
namenum = name_num(onnum, nameon)
page_point_list = page_data(data, namenum)
return page_point_list
七、获取全部数据
def main(name_list):
point_list = []
for page in range(1, 6):
point_list.extend(page_point(page))
print(point_list)
print(max(point_list))
print(name_list[point_list.index(max(point_list)) + 1])最后有一点网页里名字的索引是从1开始的，所以point的最大值索引要+1才是名字的索引。
