作者设计了一个多阶段博弈论模型来针对罕见病的不同补贴方案,分析政府、联盟、制药商和患者之间的相互作用。
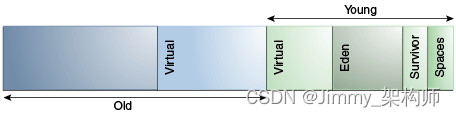
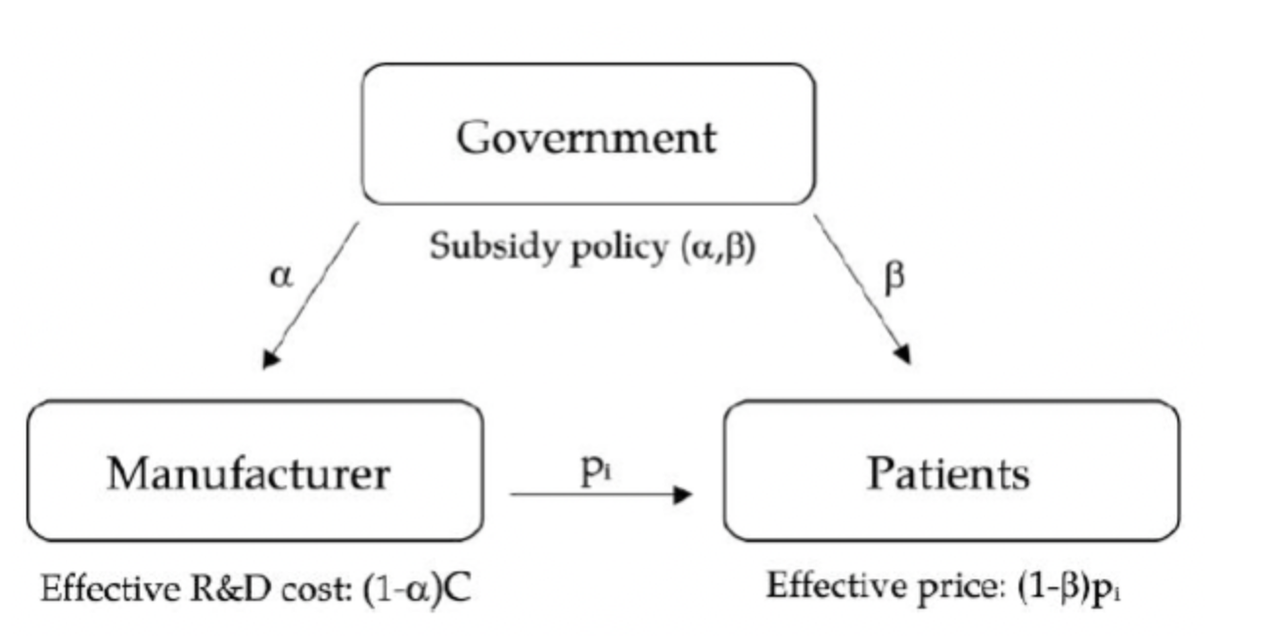
制药商补贴为 α C \alpha C αC,其中 C C C是研发成本, α ∈ [ 0 , 1 ) \alpha \in [0,1) α∈[0,1)是政府总成本的比例。患者补贴为 β p i \beta p_i βpi,其中 p i p_i pi是药品每单位售价, β \beta β是政府承担的比例。下图总结了补贴政策 ( α , β ) (\alpha,\beta) (α,β)中三者的关系。
作者的四阶段斯塔克伯格博弈基于以下事件:
- (补贴决策)在预算为 B B B的情况下,政府作为领导者选择制造商补贴 α \alpha α和患者补贴 β \beta β,以最大化社会福利 S = ω W + ( 1 − ω ) π m S=\omega W+(1-\omega)\pi_m S=ωW+(1−ω)πm,其中 ω \omega ω是对患者福利的相对重视程度。
- (药物开发决策)制药商作为追随者,根据有效率 e i e_i ei(患者治疗成功的概率)的不确定性决定是否开发药物。如果制药商以研发成本 C C C开发药物,则实现的高成功率 e h e_h eh的概率为 q q q,低成功率 e ℓ e_ℓ eℓ的概率为 ( 1 − q ) (1-q) (1−q)。
- (定价决策)在内生定价方案下,制造商确定价格;在外生定价方案下,联盟确定价格 p i p_i pi,其中 i ∈ { h , ℓ } i ∈ \{h, ℓ\} i∈{h,ℓ}表示有效率的高或低。
- (购买决策)如果药物由制药商开发,那么患者根据患者补贴 β β β和价格 p i p_i pi做出购买决策。(制药商收到的付款取决于采用的支付方案(即基于销售或基于结果)
鉴于两种定价方案(即内生和外生)和两种支付方案(即(1)基于销售和(2)基于结果),作者分别搭建了4种情况的模型。
- 在基于销售的支付方案下,作者运用逆向归纳法得到预期需求和预期患者福利:
d i ( p i , β ) = { v ˉ e i − x i ( 1 − β ) p i v ˉ e i if v ˉ e i ≥ x i ( 1 − β ) p i , 0 otherwise. W i ( p i , β ) = ∫ x i ( 1 − β ) p i e i v ˉ [ v e i − x i ( 1 − β ) p i ] ⋅ 1 v ˉ d v = ( v ˉ e i − x i ( 1 − β ) p i ) 2 2 v ˉ e i . \begin{gathered} d_i\left(p_i, \beta\right)= \begin{cases}\frac{\bar{v} e_i-x_i(1-\beta) p_i}{\bar{v} e_i} & \text { if } \bar{v} e_i \geq x_i(1-\beta) p_i, \\ 0 & \text { otherwise. }\end{cases} \\ W_i\left(p_i, \beta\right)=\int_{\frac{x_i(1-\beta) p_i}{e_i}}^{\bar{v}}\left[v e_i-x_i(1-\beta) p_i\right] \cdot \frac{1}{\bar{v}} d v \\ =\frac{\left(\bar{v} e_i-x_i(1-\beta) p_i\right)^2}{2 \bar{v} e_i} . \end{gathered} di(pi,β)={vˉeivˉei−xi(1−β)pi0 if vˉei≥xi(1−β)pi, otherwise. Wi(pi,β)=∫eixi(1−β)pivˉ[vei−xi(1−β)pi]⋅vˉ1dv=2vˉei(vˉei−xi(1−β)pi)2.
a)当内生定价时,政府的优化问题是要在预算约束 B B B和制造商的参与约束 π m ( α , β ) ≥ 0 \pi_m(\alpha, \beta) \geq 0 πm(α,β)≥0 的情况下,最大化 S S S:
π g = max α , β S = max α , β { ω ⋅ ( q e h + ( 1 − q ) e ℓ ) v ˉ 8 + ( 1 − ω ) . ( ( q e h x ℓ + ( 1 − q ) e ℓ x h ) v ˉ 4 ( 1 − β ) x h x ℓ − ( 1 − α ) C ) } s.t. α C + β ( q e h x ℓ + ( 1 − q ) e ℓ x h ) v ˉ 4 ( 1 − β ) x h x ℓ ≤ B , ( q e h x ℓ + ( 1 + q ) e ℓ x h ) v ˉ 4 ( 1 − β ) x h x ℓ − ( 1 − α ) C ≥ 0 , α , β ∈ [ 0 , 1 ) . \begin{array}{r} \pi_g=\max _{\alpha, \beta} S=\max _{\alpha, \beta}\left\{\omega \cdot \frac{\left(q e_h+(1-q) e_{\ell}\right) \bar{v}}{8}+(1-\omega) .\right. \\ \left.\quad\left(\frac{\left(q e_h x_{\ell}+(1-q) e_{\ell} x_h\right) \bar{v}}{4(1-\beta) x_h x_{\ell}}-(1-\alpha) C\right)\right\} \\ \text { s.t. } \alpha C+\frac{\beta\left(q e_h x_{\ell}+(1-q) e_{\ell} x_h\right) \bar{v}}{4(1-\beta) x_h x_{\ell}} \leq B, \\ \frac{\left(q e_h x_{\ell}+(1+q) e_{\ell} x_h\right) \bar{v}}{4(1-\beta) x_h x_{\ell}}-(1-\alpha) C \geq 0, \\ \alpha, \beta \in[0,1) . \end{array} πg=maxα,βS=maxα,β{ω⋅8(qeh+(1−q)eℓ)vˉ+(1−ω).(4(1−β)xhxℓ(qehxℓ+(1−q)eℓxh)vˉ−(1−α)C)} s.t. αC+4(1−β)xhxℓβ(qehxℓ+(1−q)eℓxh)vˉ≤B,4(1−β)xhxℓ(qehxℓ+(1+q)eℓxh)vˉ−(1−α)C≥0,α,β∈[0,1).
作者发现政府的最优补贴分配政策并不是唯一的。当预算约束得到满足时,政府可以仅对制造商进行补贴,仅对患者进行补贴,或者对制造商和患者进行补贴。仅对患者补贴和另外两种分配政策相比并不会提升预期患者福利,因为在内生定价下制造商会将患者补贴纳入定价之中。
b) 在外生定价时,根据模型可以发现,当研发成本
C
C
C特别高时,如果政府的补贴不足,制药厂将不会开发该药物。另一个发现是,外生定价下的最优补贴是唯一的,并且取决于治疗具有高效率的概率
q
q
q。当概率
q
q
q相对较高时,政府应仅对制造商进行补贴,否则应对患者进行补贴(或两者都进行)。
π
g
=
max
α
,
β
S
=
max
α
,
β
{
ω
⋅
(
q
(
2
(
1
−
λ
)
e
h
+
(
1
−
β
)
λ
x
h
)
2
v
ˉ
32
(
1
−
λ
)
2
e
h
+
(
1
−
q
)
(
2
(
1
−
λ
)
e
ℓ
+
(
1
−
β
)
λ
x
ℓ
)
2
v
ˉ
32
(
1
−
λ
)
2
e
ℓ
)
+
(
1
−
ω
)
⋅
(
(
q
e
h
x
ℓ
+
(
1
−
q
)
e
ℓ
x
h
)
v
ˉ
4
(
1
−
β
)
x
h
x
ℓ
−
(
q
e
ℓ
x
h
+
(
1
−
q
)
e
h
x
ℓ
)
(
1
−
β
)
λ
2
v
ˉ
16
(
1
−
λ
)
2
e
h
e
ℓ
−
(
1
−
α
)
C
)
}
,
s.t.
α
C
+
β
(
q
e
h
x
ℓ
+
(
1
−
q
)
e
ℓ
x
h
)
v
ˉ
4
(
1
−
β
)
x
h
x
ℓ
−
β
(
q
e
ℓ
x
h
+
(
1
−
q
)
e
h
x
ℓ
)
(
1
−
β
)
λ
2
v
ˉ
16
(
1
−
λ
)
2
e
h
e
ℓ
≤
B
,
(
q
e
h
x
ℓ
+
(
1
−
q
)
e
ℓ
x
h
)
v
ˉ
4
(
1
−
β
)
x
h
x
ℓ
−
(
q
e
ℓ
x
h
+
(
1
−
q
)
e
h
x
ℓ
)
(
1
−
β
)
λ
2
v
ˉ
16
(
1
−
λ
)
2
e
h
e
ℓ
−
(
1
−
α
)
C
≥
0
,
α
,
β
∈
[
0
,
1
)
.
\begin{aligned} \pi_g= & \max _{\alpha, \beta} S \\ = & \max _{\alpha, \beta}\left\{\omega \cdot \left(\frac{q\left(2(1-\lambda) e_h+(1-\beta) \lambda x_h\right)^2 \bar{v}}{32(1-\lambda)^2 e_h}\right.\right. \\ & \left.+\frac{(1-q)\left(2(1-\lambda) e_{\ell}+(1-\beta) \lambda x_{\ell}\right)^2 \bar{v}}{32(1-\lambda)^2 e_{\ell}}\right) \\ & +(1-\omega) \cdot\left(\frac{\left(q e_h x_{\ell}+(1-q) e_{\ell} x_h\right) \bar{v}}{4(1-\beta) x_h x_{\ell}}\right. \\ & \left.\left.-\frac{\left(q e_{\ell} x_h+(1-q) e_h x_{\ell}\right)(1-\beta) \lambda^2 \bar{v}}{16(1-\lambda)^2 e_h e_{\ell}}-(1-\alpha) C\right)\right\}, \\ & \text { s.t. } \alpha C+\frac{\beta\left(q e_h x_{\ell}+(1-q) e_{\ell} x_h\right) \bar{v}}{4(1-\beta) x_h x_{\ell}} \\ & -\frac{\beta\left(q e_{\ell} x_h+(1-q) e_h x_{\ell}\right)(1-\beta) \lambda^2 \bar{v}}{16(1-\lambda)^2 e_h e_{\ell}} \leq B, \\ & \frac{\left(q e_h x_{\ell}+(1-q) e_{\ell} x_h\right) \bar{v}}{4(1-\beta) x_h x_{\ell}} \\ & -\frac{\left(q e_{\ell} x_h+(1-q) e_h x_{\ell}\right)(1-\beta) \lambda^2 \bar{v}}{16(1-\lambda)^2 e_h e_{\ell}}-(1-\alpha) C \geq 0, \\ & \alpha, \beta \in[0,1) . \end{aligned}
πg==α,βmaxSα,βmax{ω⋅(32(1−λ)2ehq(2(1−λ)eh+(1−β)λxh)2vˉ+32(1−λ)2eℓ(1−q)(2(1−λ)eℓ+(1−β)λxℓ)2vˉ)+(1−ω)⋅(4(1−β)xhxℓ(qehxℓ+(1−q)eℓxh)vˉ−16(1−λ)2eheℓ(qeℓxh+(1−q)ehxℓ)(1−β)λ2vˉ−(1−α)C)}, s.t. αC+4(1−β)xhxℓβ(qehxℓ+(1−q)eℓxh)vˉ−16(1−λ)2eheℓβ(qeℓxh+(1−q)ehxℓ)(1−β)λ2vˉ≤B,4(1−β)xhxℓ(qehxℓ+(1−q)eℓxh)vˉ−16(1−λ)2eheℓ(qeℓxh+(1−q)ehxℓ)(1−β)λ2vˉ−(1−α)C≥0,α,β∈[0,1).
2. 在基于结果的支付方式下,由于当药物不起作用时,患者和政府无需支付费用,患者是风险中性行为。同样运用逆向归纳法得到预期需求和预期患者福利:
d
i
(
p
i
,
β
)
=
{
v
ˉ
−
(
1
−
β
)
p
i
v
ˉ
if
(
1
−
β
)
p
i
≤
v
ˉ
,
0
otherwise.
W
(
p
i
,
β
)
=
∫
(
1
−
β
)
p
i
v
ˉ
e
i
(
v
−
(
1
−
β
)
p
i
)
d
v
⋅
1
v
ˉ
=
e
i
(
v
ˉ
−
(
1
−
β
)
p
i
)
2
2
v
ˉ
.
\begin{aligned} & d_i\left(p_i, \beta\right)= \begin{cases}\frac{\bar{v}-(1-\beta) p_i}{\bar{v}} & \text { if }(1-\beta) p_i \leq \bar{v}, \\ 0 & \text { otherwise. }\end{cases} \\ & W\left(p_i, \beta\right)=\int_{(1-\beta) p_i}^{\bar{v}} e_i\left(v-(1-\beta) p_i\right) d v \cdot \frac{1}{\bar{v}} \\ &=\frac{e_i\left(\bar{v}-(1-\beta) p_i\right)^2}{2 \bar{v}} . \end{aligned}
di(pi,β)={vˉvˉ−(1−β)pi0 if (1−β)pi≤vˉ, otherwise. W(pi,β)=∫(1−β)pivˉei(v−(1−β)pi)dv⋅vˉ1=2vˉei(vˉ−(1−β)pi)2.
a) 在内生定价时,基于结果的支付方案所涉及的政府问题实质上是与基于销售的支付方案的问题的一个特例。这是因为在此情况下,患者不承担任何风险,因此患者的风险规避系数 γ γ γ对患者福利和制药厂的预期利润没有影响。当价格由制药商内生确定时,最优补贴分配政策的结构特征与基于销售的情况相同。由于在药物无效时制造商不从患者那里收到任何付款,因此在基于结果的支付方案下,风险从患者转移到了制造商身上。这种风险转移导致制造商提高价格以抵消治疗失败的患者的损失利润。
b) 在外生定价时,政府的问题是基于销售的支付方案下且外生定价时政府问题的一个特例(即 γ = 1 \gamma =1 γ=1)。因此,最优补贴政策的结构在基于结果的支付下仍然成立。
药品的供应链管理 | Stockpiling at the Onset of the COVID-19 Pandemic: An Empirical Analysis of National Prescription Drug Sales and Prices
Reference: Park, Minje, et al. “Stockpiling at the Onset of the COVID-19 Pandemic: An Empirical Analysis of National Prescription Drug Sales and Prices.” Management Science (2023).
原文链接: https://doi.org/10.1287/mnsc.2021.04150
Problem
在COVID-19的早期阶段,很多美国的医院报告了COVID-19患者所使用的处方药短缺。如何在疫情或其他公共卫生紧急情况爆发初期更好地缓解基本医疗产品短缺是至关重要的,因为短缺可能会延迟医疗服务,增加成本,甚至危及患者的生命。疫情期间医疗产品短缺通常被归因于供应链方面的因素。例如,医疗口罩和其他所需物资的短缺被归因于受到减少的劳动力、减少从制造这些产品的国家的出口以及质量问题引起的供应不足。国际出口禁令进一步限制了进口到美国的商品。例如,英国禁止出口82种药物,印度限制了26种活性药用成分和成品药品的出口。需求方的行为可能也导致医疗产品的短缺。一些文章将纽约地区COVID-19处方药的短缺归因于尚未受到COVID-19影响的地区的医院囤积基本物资。医疗保健供应链的特点使其难以应对对医疗产品需求的意外变化。处方药的生产需要大量的前期成本,且在美国市场销售处方药,供应商必须遵守严格的联邦法规,确保在获批时符合安全性和功效,并且必须根据当前良好的生产规范制造药品。这些市场特征可能会触发医院的囤积行为,因为他们认为可能无法轻松解决的潜在的供应短缺。预期囤积行为,处方药供应商还可能大幅度提高现有库存的价格,这被称为价格操纵(price gouging)。尽管有相关建议,关于医疗产品的囤积和价格操纵并没有严谨的研究。本文将实证检验COVID-19相关药物的销售、价格和供应短缺及囤积药物之间的关系。
Method
作者从FDA的基本药物清单中确定了COVID-19相关药物(暴露组),作者同时确定了一组与COVID-19无关的处方药(对照组),以控制疫情期间非COVID-19医疗服务需求的变化。本研究中共有106种样本药物,其中55种在暴露组,51种在对照组。
作者实证性地检验了COVID-19相关药物在疫情的早期阶段,即从2020年3月到9月,销售量和价格是否发生了统计学上显著的变化。其中关键结果变量是药物的销售量(UnitsSold),定义为在一个月内销售出的药物总单位。为检验变化,作者建立了一个双重差分模型,将COVID-19相关药品在疫情爆发前平行销售趋势的对照药品作为参照,能够更准确地确定COVID-19药品的销售量:
Y
i
c
m
y
=
α
i
+
β
1
Post
m
y
+
β
2
Exposure
i
×
Post
m
y
+
γ
Category
i
×
Trend
m
y
+
δ
X
i
c
m
y
+
λ
m
+
θ
c
+
ε
i
c
m
y
.
\begin{aligned} Y_{i c m y}= & \alpha_i+\beta_1 \text { Post }_{m y}+\beta_2 \text { Exposure }_i \times \text { Post }_{m y} \\ & +\gamma \text { Category }_i \times \text { Trend }_{m y}+\boldsymbol{\delta} \boldsymbol{X}_{i c m y} \\ & +\lambda_m+\theta_c+\varepsilon_{i c m y} . \end{aligned}
Yicmy=αi+β1 Post my+β2 Exposure i× Post my+γ Category i× Trend my+δXicmy+λm+θc+εicmy.
其中
Y
i
c
m
y
Y_{icmy}
Yicmy是
U
n
i
t
s
S
o
l
d
i
c
m
y
UnitsSold_{icmy}
UnitsSoldicmy和
P
r
i
c
e
i
c
m
y
Price_{icmy}
Priceicmy的结果变量,
P
o
s
t
m
y
Post_{my}
Postmy是一个指示变量,如果月份-年份在 COVID-19 开始后(从 2020 年 3 月)则为 1,否则为0。
作者进一步分析了在疫情早期阶段每月处方药销售和价格的变化。为了比较每个月的变化,作者假设非COVID-19药品的销售和价格在疫情后期的每个月都保持一致。作者用一组指示变量替换了
P
o
s
t
m
y
Post_{my}
Postmy变量,新的双重差分模型如下:
Y
i
c
m
y
=
α
i
+
∑
m
y
∈
Post
ϕ
m
y
PostMonth
m
y
+
∑
m
y
∈
Post
β
m
y
Exposure
i
×
PostMonth
m
y
+
γ
Category
i
×
Trend
m
y
+
δ
X
i
c
m
y
+
λ
m
+
θ
c
+
ε
i
c
m
y
,
\begin{aligned} & Y_{i c m y}=\alpha_i+\sum_{m y \in \text { Post }} \phi_{m y} \text { PostMonth }_{m y} \\ & +\sum_{m y \in \text { Post }} \beta_{m y} \text { Exposure }_i \times \text { PostMonth }_{m y} \\ & +\boldsymbol{\gamma} \text { Category }_i \times \text { Trend }_{m y}+\boldsymbol{\delta} \boldsymbol{X}_{i c m y} \\ & +\lambda_m+\theta_c+\varepsilon_{i c m y}, \end{aligned}
Yicmy=αi+my∈ Post ∑ϕmy PostMonth my+my∈ Post ∑βmy Exposure i× PostMonth my+γ Category i× Trend my+δXicmy+λm+θc+εicmy,
其中
P
o
s
t
M
o
n
t
h
m
y
PostMonth_{my}
PostMonthmy为新的指示变量,表示疫情后期的每一个月。
Summary of Results
销售数量:根据统计数据,对照组药物销量在疫情初期显著下降,而曝光组药物仅在2020年3月和4月有所增长。COVID-19患者护理药物销售主要集中在这两个月,之后迅速减少。疫情初期,对照组药物销量减少表明非COVID-19需求下降。而COVID-19药物的销售主要出现在疫情初期,暗示了药品囤积现象。
药品价格:作者接着分析了疫情初期在美国医院的药品价格的变化,结果表明对照组和曝光组药物价格变化并不显著。竞争可能限制了价格上涨,与FDA的先前发现一致。
供应短缺:疫情初期由于囤积导致的需求突然增加引发了全国性的供应短缺。首先,这些暴露组药物的短缺始于2020年4月,即销售量的突然增加之后。
囤积与供应短缺的关系:作者计算得出的平均边际效应显示,销量增加1%,供应短缺的概率提高1.3% ( p < 0.001 ) (p < 0.001) (p<0.001)。

根据文中的分析,尽管需求增加,与COVID-19相关的药品价格并没有显著上涨。一方面,价格保持平稳确保了疫情期间必需药品的可负担性。另一方面,也可能会加剧短缺,因为理论上,价格上涨会阻止买家囤积,并激励供应商增加生产。作者建议政策制定者可以考虑提供额外的激励,以鼓励制药商增加所需药品的生产。