【题目来源】
https://www.luogu.com.cn/problem/P1377
【题目描述】
众所周知，二叉查找树的形态和键值的插入顺序密切相关。准确的讲：
1.空树中加入一个键值 k，则变为只有一个结点的二叉查找树，此结点的键值即为 k。
2.在非空树中插入一个键值 k，若 k 小于其根的键值，则在其左子树中插入 k，否则在其右子树中插入 k。
我们将一棵二叉查找树的键值插入序列称为树的生成序列，现给出一个生成序列，求与其生成同样二叉查找树的所有生成序列中字典序最小的那个，其中，字典序关系是指对两个长度同为 n 的生成序列，先比较第一个插入键值，再比较第二个，依此类推。
【输入格式】
第一行，一个整数 n，表示二叉查找树的结点个数。
第二行，有 n 个正整数 k1,k2,⋯,kn，表示生成序列，简单起见，k1∼kn 为一个 1 到 n 的排列。
【输出格式】
一行，n 个正整数，为能够生成同样二叉查找树的所有生成序列中最小的。
【输入样例】
4
1 3 4 2
【输出样例】
1 3 2 4
【数据范围及约定】
对于 20% 的数据，1≤n≤10。
对于 50% 的数据，1≤n≤100。
对于 100% 的数据，1≤n≤10^5。
【算法分析】
● 本质上，满足本题题设条件的其实就是笛卡尔树。针对本题，构建完笛卡尔树后，对其进行先序遍历便可得到所求结果。
例如，按照题设规则，即“左小右大”规则，对本题样例 1，3，4，2 构建生成的二叉查找树如下所示。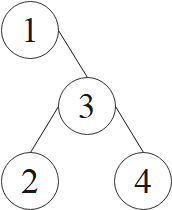
然后，对此图进行先序遍历，可得到输出 1，3，2，4。
● 笛卡尔树是一种非常特殊的二叉搜索树（BST）。每个结点有两个信息 (pri, val)，如果只考虑 pri，它是一棵二叉搜索树，如果只考虑 val，它是一个小根堆。注意，本题读入的是结点的 val。
● 字典序最小的构造方法肯定是从小到大插入结点，但最后构建出来的树会退化成一条链。
● 如何构建笛卡尔树？
据笛卡尔树结点信息可知，笛卡尔树是具有双权重 (pri, val) 的树。那么，如何构建笛卡尔树？实践过程中，常见解决方案是借助“单调栈”这种数据结构。
单调栈中数据递增或递减。笛卡尔树需要构建小根堆，故需维护单调栈中的数据递减。
● 构造笛卡尔树时，若各个结点指定了 pri，则先对 pri 从小到大排列。否则，pri 默认为数组下标。然后，依据 pri 顺序将结点逐个插入到笛卡尔树中。
● 单调栈：https://blog.csdn.net/hnjzsyjyj/article/details/117370314
单调栈是一种非常适合处理“下一个更大元素（Next Greater Number）”问题的数据结构。
● 快读：https://blog.csdn.net/hnjzsyjyj/article/details/120131534
在数据量比较大的时候，即使使用 scanf 函数读入数据也会超时，这时就需要使用“快读”函数了。“快读”函数之所以快，是因为其中的 getchar 函数要比 scanf 函数快。 网传，“快读”函数能以比 scanf 函数快5倍的速度读入任意整数。
貌似，笛卡尔树问题常用到快读。
● 本题代码与 https://blog.csdn.net/hnjzsyjyj/article/details/138353654 及其相似，可对比学习。
【算法代码】
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=1e5+5;
int a[maxn];
int n;
LL lson[maxn],rson[maxn];
stack<int> s;
int read() { //fast read
int x=0,f=1;
char c=getchar();
while(c<'0' || c>'9') { //!isdigit(c)
if(c=='-') f=-1; //- is a minus sign
c=getchar();
}
while(c>='0' && c<='9') { //isdigit(c)
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
void print(int x) {
if(x==0) return;
cout<<x<<" ";
print(lson[x]);
print(rson[x]);
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++) {
int id;
id=read();
a[id]=i;
}
for(int i=1; i<=n; i++) {
while(!s.empty() && a[s.top()]>a[i]) {
lson[i]=s.top();
s.pop();
}
if(!s.empty()) rson[s.top()]=i;
s.push(i);
}
int root;
while(!s.empty()) {
root=s.top();
s.pop();
}
print(root);
return 0;
}
/*
in:
4
1 3 4 2
out:
1 3 2 4
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/138353654
https://blog.csdn.net/hnjzsyjyj/article/details/138353654
https://blog.csdn.net/liufengwei1/article/details/107866930
https://www.cnblogs.com/LSlzf/p/11150484.html
https://www.cnblogs.com/yinyuqin/p/15000037.html
https://zhuanlan.zhihu.com/p/674774129
