1.情景导入

你应该知道斐波那契数列吧！就是前两项之和等于这一项。如果你学过递归，你肯定会写这道题：输入一个N代表你要求的项数，然后输出斐波那契的第N项。这道题看似简单，实则也挺简单实则特别困难（对于大数据来说）。

下面是一段斐波纳契的代码：

#include <iostream>
using namespace std;
long long f(long long n) {
    if (n < 3){
    	return 1;
	}
	return f(n-1)+f(n-2);
}

int main(){
    long long n;
    cin >> n;
    cout << f(n);
    return 0;
}

 如果我们用C++运行这段代码，你会发现如果我们输入50，它就会加载很久。

肯定会超时！！！！！！！！！！！！！！！！！！！！！！！！！！！！！(っ °Д °;)っ

所以今天我们要学习一种时间复杂度很低的方法！\(￣︶￣*\))

2.导入概念

首先我会向你提出一个问题:是什么原因会导致递归速度这么慢?

如果我们按照计算机的方法去思考, 你会发现重复计算的地方太多了!

大家请看下图:

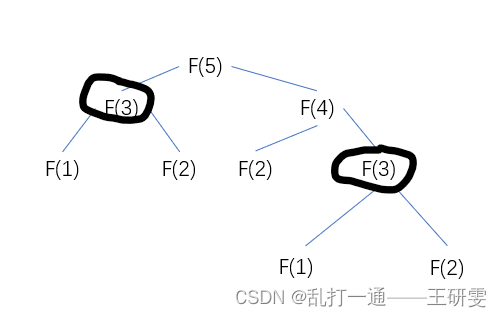
 在图片上有人计算机的方法给大家演示出来了如果我们要求斐波那契的第五项,计算机内部会是怎样运算.在这么小的例子中居然重复计算了两次斐波那契的第三项,那你想象一下如果斐波那契的项数不断增加求成了五十,重复计算的个数会越来越多,我们这种方法不再重复计算.

大概意思

我们可以用一个数组来递归,一开始数组的一号位和二号位默认为一.如果数组的第N号位有东西,也就是已经计算过了,那之间返回这一号位的值,如果没有,按照原来的方法进行计算(一定要赋值给我们的数组中).

简简单单的动态规划思路,计算过的就不再计算了(❤️ ω ❤️)

代码

直接公布

#include <iostream>
using namespace std;
long long d[100000] = {0,1,1};
long long f(long long n) {
    if (d[n] != 0){
        return d[n];
    }
    return d[n] = f(n-1)+f(n-2);
}

int main(){
    long long n;
    cin >> n;
    cout << f(n);
    return 0;
}

//一定要开long long

3.例题

题目名称：数字三角形

数字三角形，从三角形顶部往下走，只能往左下或右下走，求走到最下面时所经过的数字和最大为多少？（下图为n=6时的情况)

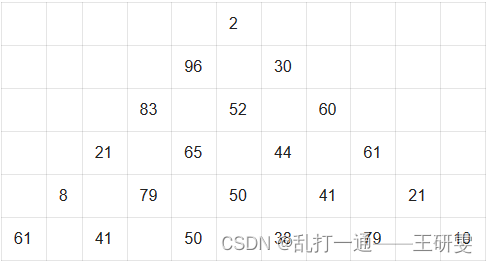
输入描述

第1行：整数n(1<=n<=1000)

第2-n+1行：每行若干整数，第i行有i-1个整数，空格分隔。

输出描述

一行：一个整数，表示所经过数字的最大和。

样例1

输入

6
2
96 30
83 52 60
21 65 44 61
8 79 50 41 21
61 41 50 38 79 10

 

输出

375

1.先做一遍样例 

从2开始, 96 > 30,83 > 52,65 > 21,79 > 50,50>41;

所以最终的式子是:2+96+83+65+79+50=375

2.思路

这回重复的就是路径,我们会把路径中元素的和储存在一个名字叫做D的数组中,从顶部开始，判断底下两条路径的最大值，调用自身函数进行递归。到达下一个节点再进行求最大值，如果这个节点以前算过那就不算直接返回d的这一号位.

3.代码

#include <bits/stdc++.h>
using namespace std;
int d[1005][1005];
int a[1005][1005];
    int n;
int s(int i, int j){
    if (d[i][j] >= 0){
        return d[i][j];
    }
    return d[i][j] = a[i][j]+(i==n+1?0:max(s(i+1,j),s(i+1,j+1)));
}
int main(){
    cin >> n;
    memset(d,-1,sizeof(d[0][0])*1005*1005);  //初始化设为负一
    for (int i =1; i <= n+1; i++){
        for (int j =1; j < i; j++){
            cin >> a[i][j];
        }
    }
    cout << s(1,1);
    return 0;
}

4.另外一种解法:递推

从底下的每一个节点和往上推，这里就不细讲了。

#include <bits/stdc++.h>
using namespace std;
int d[1005][1005];
int a[1005][1005];
int n;
int main(){
    cin >> n;
    for (int i =1; i <= n+1; i++){
        for (int j =1; j <= i; j++){
            cin >> a[i][j];
        }
    }
    for (int j =1; j <= n; j++){
        d[n][j] = a[n][j];
    }
    for (int i =n; i >= 1; i--){
        for (int j =1; j <= i; j++){
            d[i][j] = a[i][j]+max(d[i+1][j],d[i+1][j+1]);
        }
    }
    cout << d[1][1];
    return 0;
}