密度峰值聚类(DPC)算法（Python3实现）

一、密度峰值算法简介

1、密度峰值聚类算法

密度峰值聚类（Density peaks clustering, DPC）算法是由Rodriguez和Laio于2014年提出的一种聚类分析算法。其原始文献名是在在 Science上发表的，论文名称为“Clustering by Fast Search and Find of Density Peaks”。这种聚类方法该算法是一种基于密度的聚类算法，可以自动确定聚类中心和聚类的数量并适用于处理各种形状和分布的数据集

2、密度峰值聚类算法基本思想

密度峰值聚类算法要具备两个基本假设条件

聚类中心的局部密度要远远大于其临近区域数据的局部密度；
密度较高的数据对象，聚类中心离它的距离相对较远。

密度峰值聚类的核心是找出最佳聚类中心，为此密度峰值聚类算法引入了
局部密度ρ 和相对距离δ两个概念。

局部密度ρ：数据点x_i的局部密度为在截断距离(d_c)内其他数据点的数量，其中d_c是截断距离，通常取数据集样本总数1%至2%作为d_c的设定值。
这就意味着如果在这个距离内有更多的数据点，那么数据点i的局部密度就会更大。常见的局部密度的计算方式有很两种，分别为使用截断核计算方式（离散）和使用高斯核函数计算（连续）。
两种方式的计算公式分别如下：
（1）截断核
$\rho(i) = \sum_{j=1,j \neq i}^n \chi(d_{ij} - d_{c})$
$\chi(x)=\left\{ \begin{aligned} 1 & ,\ x<0 \\ 0 & ,\ x\geq 0 \end{aligned} \right.$
（2）高斯核
$\rho(i) = \sum_{j=1,j \neq i}^n exp[ ( \frac{ d_{ij}} { d_{c} } )^2]$
其中d_ij为第i个数据与第j个数据的距离，d_c为截断距离。
相对距离δ：某个数据点到比它密度更大的最近那个数据点的距离为此数据的相对距离。
如果没有比数据点x_i密度更大的数据点，那么我们将其相对距离定义为到所有其他数据点的最大距离，即
$\delta(i) = \max_{j} (d_{ij}) $
对于其余数据点，相对距离定义为：
$\delta(i) = \min_{j: \rho(j) > \rho(i)} (d_{ij}) $

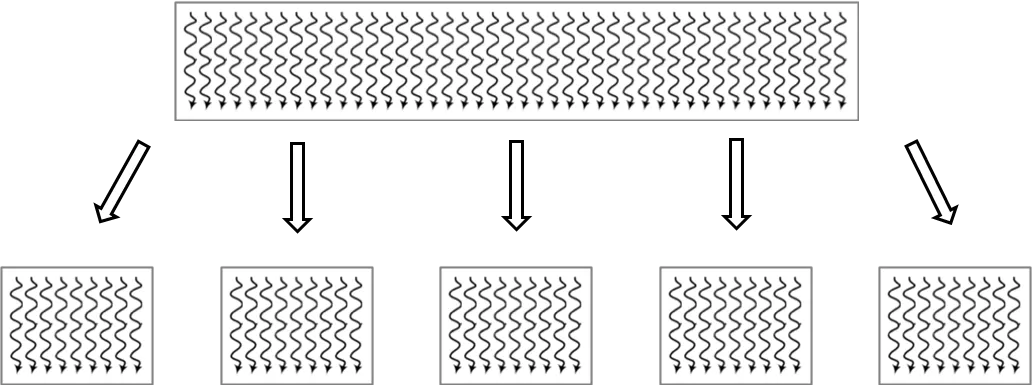
密度峰值聚类方法的核心思想是基于两个假设生成一个以ρ为横轴，δ为纵轴的图作为决策图(desision graph)，并通过决策图找到聚类中心，然后将其余的数据分别分配到距离最近的聚类中心。
在决策图中需要选择数据集中 ρ值，δ值都较大的数据对象作为聚类中心。如果某个数据δ值都大而 ρ值却较小，那么它有可能是离群点。
数据点分布
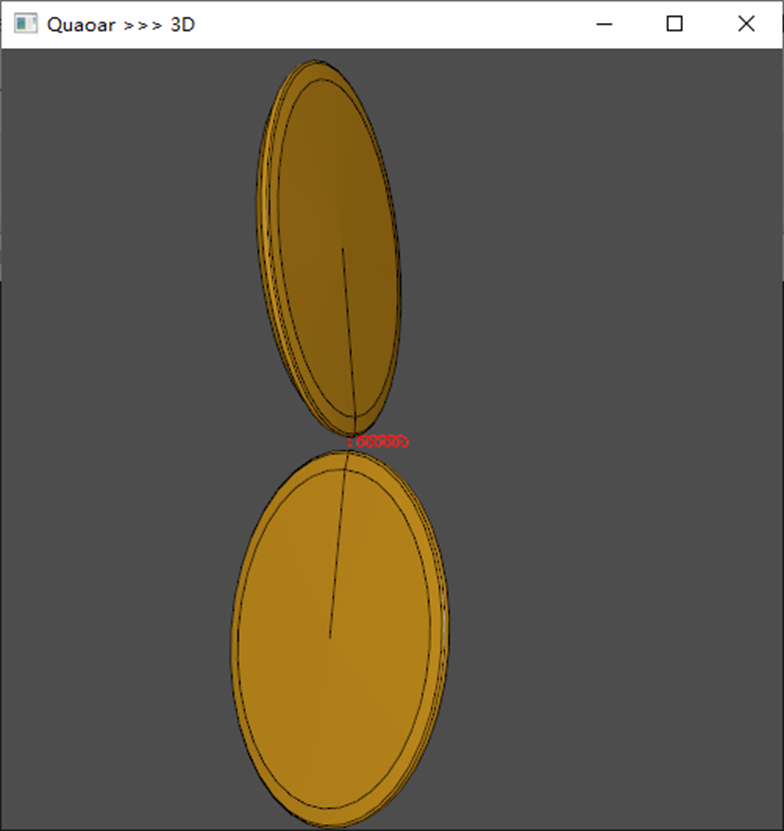
在上图的数据集中，计算局部密度和相对距离后构造的决策图如下：

通过上面的决策图可以很轻松的看出来点1和点10分别是两个聚类中心，而点26、点27和点28为离群点（噪声点）。

3、密度峰值聚类算法实现步骤

输入：数据集 $X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right.$
输出：聚类中心 $C=[c_1,c _2,…,c_k]$
Step1. 计算数据集 $X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right.$ 中所有样本点之间的欧式距离，构建相似度矩阵，并对这些距离进行降序排序，选取前 2%大小的距离作为截断距离d_c；
Step2. 根据相似度矩阵和截断距离d*_c ，并结合局部密度与相对距离公式计算数据集 X 中所有样本点的局部密度ρ 和相对距离 δ ；
Step3. 根据局部密度ρ 和相对距离δ 绘制决策图；
Step4. 根据决策图选择聚类中心；
Step5. 将剩余的样本点，按照局部密度从大到小的顺序排序，依次将其分
配给局部密度比其大的最近点所在的簇。
在这里插入图片描述

4、密度峰值聚类算法伪代码

输入：数据集 $X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right.$
输出：聚类中心 $C=[c_1,c _2,…,c_k]$ ，聚类结果CL

begin
01.n ← size(X) ;  //  计算距离矩阵 
02.for i ←1 to n do  
03.     for j ←1 to n do  
04.          calculate dij // 计算xi到xj的距离(distance from xi to xj)
05.     end for  
06.end for  
07.for i ← 1 to n do  
08.     calculate ρi // 计算xi的局部密度
09.end for
10.quick_sort(X, ρ,'desc') //  将数据集 X 根据局部密度降序排列 
11.calculate δ0 // 计算最大密度数据的相对距离
12.for i ← 1 to n do
13.     calculate δ  // 计算其余样本点的相对距离 
14. end for    
15.draw desision graph  // 基于局部密度值和相对距离值构造决策图
16.for i ← 1 to n do
17.     if ρi > ε  and δ > ε then // 如果样本点xi位于决策图的右上角
18.     C ← xi // 决策图右上角的样本点标记为聚类中心并加入集合C
19.     end if
20. end for  
21.for i ←0 to C.length do  
22.     CL(i) ← CL(nearest higher density neighbor)  // 分配剩余点 
23.end for  
24. return CL ; 
end

5、密度峰值聚类算法时间复杂度分析

假设给定数据规模为n，DPC 算法在求解相似度矩阵时的时间复杂度为O(n²) ；计算样本点的局部密度ρ 和相对距离δ 的时间复杂度为O(n²) ；所以 DPC 算法总的时间复杂度为O(n²) 。

6、密度峰值聚类算法优缺点

密度峰值聚类算法优点

不需要预先设定聚类数量；
能发现任意形状的聚类；
具有较好的噪声抗性。

密度峰值聚类算法缺点

样本点的局部密度基于截断距离d_c，并没有考虑到其邻域内样本点的分布情况，因此d_c的取值对聚类结果会有较大的影响；
需要人工选取决策图右上区域内的点作为聚类中心；
计算复杂度高；
在处理密度不均数据集和复杂流型结构数据集的剩余点分配阶段，易出现因少数样本点错误分配而导致的连锁错分现象。

二、密度峰值算法实现（Python3）

本文使用的数据集为UCI数据集，分别使用鸢尾花数据集Iris、葡萄酒数据集Wine、小麦种子数据集seeds进行测试，本文从UCI官网上将这三个数据集下载下来，并放入和python文件同一个文件夹内即可。同时由于程序需要，将数据集的列的位置做出了略微改动。数据集具体信息如下表：

数据集	样本数	属性维度	类别个数
Spiral	312	2	3
Aggregation	240	2	7
Jain	373	2	2

数据集在我主页资源里有，免积分下载，如果无法下载，可以私信我。

1、Python3实现代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import normalized_mutual_info_score  # NMI
from sklearn.metrics import rand_score  # RI
from sklearn.metrics import accuracy_score  # ACC
from sklearn.metrics import f1_score  # F-measure
from sklearn.metrics import adjusted_rand_score  # ARI

# 数据保存在.csv文件中
iris = pd.read_csv("dataset/iris.csv", header=0)  # 鸢尾花数据集 Iris  class=3
wine = pd.read_csv("dataset/wine.csv")  # 葡萄酒数据集 Wine  class=3
seeds = pd.read_csv("dataset/seeds.csv")  # 小麦种子数据集 seeds  class=3
wdbc = pd.read_csv("dataset/wdbc.csv")  # 威斯康星州乳腺癌数据集 Breast Cancer Wisconsin (Diagnostic)  class=2
glass = pd.read_csv("dataset/glass.csv")  # 玻璃辨识数据集 Glass Identification  class=6
jain = pd.read_csv("dataset/Jain.csv")  # 人工数据集
spiral = pd.read_csv("dataset/spiral.csv")  # 人工数据集
flame = pd.read_csv("dataset/Flame.csv")  # 人工数据集
aggregation = pd.read_csv("dataset/Aggregation.csv")  # 人工数据集
df = spiral # 设置要读取的数据集
# print(df)
columns = list(df.columns)  # 获取数据集的第一行，第一行通常为特征名，所以先取出
features = columns[:len(columns) - 1]  # 数据集的特征名（去除了最后一列，因为最后一列存放的是标签，不是数据）
dataset = df[features]  # 预处理之后的数据，去除掉了第一行的数据（因为其为特征名，如果数据第一行不是特征名，可跳过这一步）
attributes = len(df.columns) - 1  # 属性数量（数据集维度）
original_labels = list(df[columns[-1]])  # 原始标签


# 计算数据点两两之间的距离
def getDistanceMatrix(datas):
    N, D = np.shape(datas)
    dists = np.zeros([N, N])

    for i in range(N):
        for j in range(N):
            vi = datas[i, :]
            vj = datas[j, :]
            dists[i, j] = np.sqrt(np.dot((vi - vj), (vi - vj)))
    return dists


# 找到密度计算的阈值dc
# 要求平均每个点周围距离小于dc的点的数目占总点数的1%-2%
def select_dc(dists):
    N = np.shape(dists)[0]
    tt = np.reshape(dists, N * N)
    percent = 2.0
    position = int(N * (N - 1) * percent / 100)
    dc = np.sort(tt)[position + N]
    return dc


# 计算每个点的局部密度
def get_density(dists, dc, method=None):
    N = np.shape(dists)[0]
    rho = np.zeros(N)

    for i in range(N):
        if method == None:
            rho[i] = np.where(dists[i, :] < dc)[0].shape[0] - 1
        else:
            rho[i] = np.sum(np.exp(-(dists[i, :] / dc) ** 2)) - 1
    return rho


# 计算每个数据点的密度距离
# 即对每个点，找到密度比它大的所有点
# 再在这些点中找到距离其最近的点的距离
def get_deltas(dists, rho):
    N = np.shape(dists)[0]
    deltas = np.zeros(N)
    nearest_neiber = np.zeros(N)
    # 将密度从大到小排序
    index_rho = np.argsort(-rho)
    for i, index in enumerate(index_rho):
        # 对于密度最大的点
        if i == 0:
            continue

        # 对于其他的点
        # 找到密度比其大的点的序号
        index_higher_rho = index_rho[:i]
        # 获取这些点距离当前点的距离,并找最小值
        deltas[index] = np.min(dists[index, index_higher_rho])

        # 保存最近邻点的编号
        index_nn = np.argmin(dists[index, index_higher_rho])
        nearest_neiber[index] = index_higher_rho[index_nn].astype(int)

    deltas[index_rho[0]] = np.max(deltas)
    return deltas, nearest_neiber


# 选取rho与delta乘积较大的点作为聚类中心
def find_centers(rho, deltas, K=0):
    if K == 0:
        # 没有手动设置聚类数K，通过阈值选取rho与delta都大的点
        rho_threshold = (np.min(rho) + np.max(rho)) / 2
        delta_threshold = (np.min(deltas) + np.max(deltas)) / 2
        N = np.shape(rho)[0]
        centers = []
        for i in range(N):
            if rho[i] >= rho_threshold and deltas[i] > delta_threshold:
                centers.append(i)
        return np.array(centers)
    else:
        # 手动输入聚类数K，选取rho与delta乘积最大的K个点作为聚类中心，作为k个中心点
        rho_delta = rho * deltas
        centers = np.argsort(-rho_delta)
        return centers[:K]


def cluster_PD(rho, centers, nearest_neiber):
    K = np.shape(centers)[0]
    if K == 0:
        print("can not find centers")
        return

    N = np.shape(rho)[0]
    label = -1 * np.ones(N).astype(int)

    # 首先对几个聚类中进行标号
    for i, center in enumerate(centers):
        label[center] = i

    # 将密度从大到小排序
    index_rho = np.argsort(-rho)
    for i, index in enumerate(index_rho):
        # 从密度大的点进行标号
        if label[index] == -1:
            # 如果没有被标记过
            # 那么聚类标号与距离其最近且密度比其大
            # 的点的标号相同
            label[index] = label[int(nearest_neiber[index])]
    return label


def draw_decision(rho, deltas):
    plt.cla()
    for i in range(np.shape(datas)[0]):
        plt.scatter(rho[i], deltas[i], s=16., color=(0, 0, 0))
        plt.annotate(str(i), xy=(rho[i], deltas[i]), xytext=(rho[i], deltas[i]))
        plt.xlabel("rho")
        plt.ylabel("deltas")
    # plt.savefig(filename+"_decision.jpg")
    plt.show()


# 计算聚类指标
def clustering_indicators(labels_true, labels_pred):
    if type(labels_true[0]) != int:
        labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]])  # 如果标签为文本类型，把文本标签转换为数字标签
    f_measure = f1_score(labels_true, labels_pred, average='macro')  # F值
    accuracy = accuracy_score(labels_true, labels_pred)  # ACC
    normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred)  # NMI
    rand_index = rand_score(labels_true, labels_pred)  # RI
    ARI = adjusted_rand_score(labels_true, labels_pred)
    return f_measure, accuracy, normalized_mutual_information, rand_index, ARI


def draw_cluster(datas, label, centers):
    plt.cla()
    K = np.shape(centers)[0]
    colors = np.array(["blue", "red", "green", "orange", "purple", "cyan", "magenta", "beige", "hotpink", "#88c999"])
    if attributes > 2:
        datas = PCA(n_components=2).fit_transform(datas)  # 如果属性数量大于2，降维
    for i in range(K):
        plt.scatter(datas[np.nonzero(label == i), 0], datas[np.nonzero(label == i), 1], c=colors[i], s=7)
        # plt.scatter(datas[centers[i], 0], datas[centers[i], 1], color="k", marker="+", s=200.)  # 聚类中心
    # plt.savefig(file_name + "_cluster.jpg")
    # 设置x和y坐标轴刻度的标签字体和字号
    plt.xticks(fontproperties='Times New Roman', fontsize=10.5)
    plt.yticks(fontproperties='Times New Roman', fontsize=10.5)
    plt.show()


if __name__ == "__main__":

    # 主程序
    datas = np.array(dataset).astype(np.float32)
    # 计算距离矩阵
    dists = getDistanceMatrix(datas)
    # 计算dc
    dc = select_dc(dists)
    print("dc", dc)
    # 计算局部密度ρ
    rho = get_density(dists, dc, method="Gaussion")
    # 计算密度距离δ
    deltas, nearest_neiber = get_deltas(dists, rho)

    # 绘制密度/距离分布图
    draw_decision(rho, deltas)

    # 获取聚类中心点
    centers = find_centers(rho, deltas)
    print("centers", centers)

    label = cluster_PD(rho, centers, nearest_neiber)
    plt.cla()
    K = np.shape(centers)[0]
    F_measure, ACC, NMI, RI, ARI = clustering_indicators(original_labels, label)  # 计算聚类指标
    print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI, "ARI", ARI)
    draw_cluster(datas, label, centers)

2、聚类指标

本文选择了F值（F-measure，FM）、准确率（Accuracy，ACC）、标准互信息（Normalized Mutual Information，NMI）和兰德指数（Rand Index，RI）作为评估指标，其值域为[0,1]，取值越大说明聚类结果越符合预期。

F值结合了精度（Precision）与召回率（Recall）两种指标，它的值为精度与召回率的调和平均，其计算公式见公式：

$Precision=\frac{TP}{TP+FP}$

$Recall=\frac{TP}{TP+FN}$

$F-measure=\frac{2Recall \times Precision}{Recall+Precision}$

ACC是被正确分类的样本数与数据集总样本数的比值，计算公式如下：

$ACC=\frac{TP+TN}{TP+TN+FP+FN}$

其中，TP（True Positive）表示将正类预测为正类数的样本个数，TN （True Negative）表示将负类预测为负类数的样本个数，FP（False Positive）表示将负类预测为正类数误报的样本个数，FN（False Negative）表示将正类预测为负类数的样本个数。

NMI用于量化聚类结果和已知类别标签的匹配程度，相比于ACC，NMI的值不会受到族类标签排列的影响。计算公式如下：

$NMI=\frac{I\left(U,V\right)}{\sqrt{H\left(U\right)H\left(V\right)}}$

其中H(U)代表正确分类的熵，H(V)分别代表通过算法得到的结果的熵。

其具体实现代吗如下：
由于数据集中给定的正确标签可能为文本类型而不是数字标签，所以在计算前先判断数据集的标签是否为数字类型，如果不是，则转化为数字类型

def clustering_indicators(labels_true, labels_pred):
    if type(labels_true[0]) != int:
        labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]])  # 如果标签为文本类型，把文本标签转换为数字标签
    f_measure = f1_score(labels_true, labels_pred, average='macro')  # F值
    accuracy = accuracy_score(labels_true, labels_pred)  # ACC
    normalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred)  # NMI
    rand_index = rand_score(labels_true, labels_pred)  # RI
    return f_measure, accuracy, normalized_mutual_information, rand_index


F_measure, ACC, NMI, RI = clustering_indicators(labels_number, labels)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)