分治策略 --- 快排归并

news2024/11/26 23:57:35

目录

分治-快排

一、颜色分类

二、排序数组

三、数组中的第K个最大元素

四、库存管理

分治-归并

一、排序数组

二、交易逆序对的总数

三、计算右侧小于当前元素的个数

四、翻转对

分治是一种思想，也就是将大问题分解成小问题，一直分到小问题可以快速被解决为止~

分治-快排

一、颜色分类

1.题目解析

包含三种颜色的数组，将同样的颜色分到一起，并且按红白蓝排序

2.算法分析

大家可以先复习一下我的第一篇博客双指针算法中的第一道题---移动零，本质就是数组分两块！

双指针算法-CSDN博客

而本题是要将数组分三块，所以相当于用"三指针"

下标的含义:

i: 遍历数组

left: 标记0区域的最右侧

right: 标记2区域的最左侧

过程分析:

nums[i] == 0 ：swap(nums[++left], nums[i++])

nums[i] == 1 ：++i

nums[i] == 2 :  swap(nums[--right], nums[i])

注意: num[i]==2时，交换完之后不能让i++, 因为我们不清楚nums[--right]的值是几，因此还要继续判断!

3.算法代码

class Solution {
public:
    void sortColors(vector<int>& nums) 
    {
        int i = 0, left = -1, right = nums.size();
        while(i < right)
        {
            if(nums[i] == 0) swap(nums[++left], nums[i++]);
            else if(nums[i] == 1) i++;
            else swap(nums[--right], nums[i]);
        }
    }
};

二、排序数组

912. 排序数组 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/sort-an-array/1.题目解析

排序数组，升序

2.算法分析

采用分治的思想解决，选择一个基准元素key, 使得左边比key小，右边比key大，然后分治子问题, 如果采用之前快排的方法，当数组元素全都相同时，时间复杂度会退化到O(n^2), 详细分析可以看我之前的博客:

排序素来美如玉，层进理解获芳心-CSDN博客

因此我们用上道颜色划分题目“数组分三块”的思想，实现快排

过程分析:

nums[i] < key ：swap(nums[++left], nums[i++])

nums[i] == key ：++i

nums[i] == 2 :  swap(nums[--right], nums[i])

一次划分完之后，数组就如下所示: 然后递归黄色区间和紫色区间即可

当数组中全都是重复元素时，一次划分之后数组黄色区间和紫色区间就不存在了，递归结束

key的选取:

随机选取key时，时间复杂度渐进到o(nlogn)

3.算法代码

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) 
    {
        srand(time(nullptr)); //种下一颗种子
        qsort(nums, 0, nums.size()-1);
        return nums;
    }

    void qsort(vector<int>& nums, int l, int r)
    {
        //递归结束条件
        if(l >= r) return;

        //数组分三块
        int key = getRandom(nums, l, r);
        int i = l, left = l - 1, right = r + 1;
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left], nums[i++]);
            else if(nums[i] == key) i++;
            else swap(nums[--right], nums[i]);
        }
        //[l, left], [left+1, right-1] [right, r];
        qsort(nums, l, left);
        qsort(nums, right, r);
    }

    int getRandom(vector<int>& nums, int left, int right)
    {
        int r = rand();
        return nums[r % (right - left + 1) + left];
    }
};

三、数组中的第K个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/kth-largest-element-in-an-array/1.题目解析

求数组中第K大元素

2.算法分析

解法一: Top-k问题，采用堆/优先级队列解决

解法二: 快速选择算法(基于快排)

如果我们对数组分三块之后，找第K大的元素就会快很多

1. c >= k, 那么第k大于元素落在紫色区间，递归该区间即可

2. b + c >= k(1已经不满足了), 那么第k大元素落在蓝色区间，而蓝色区间值都相等，直接返回 k 即可

3. 第k大元素元素落在黄色区间，递归该区间即可， 注意此时在黄色区间找的是第k-a-b大的元素

3.算法代码

解法一: 优先级队列

class Solution 
{
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
        priority_queue<int> q(nums.begin(), nums.end());
        while(--k)
            q.pop();
        return q.top();
    }
};

解法二: 快速选择算法

class Solution 
{
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
        srand(time(nullptr));
        return qsort(nums, 0, nums.size()-1, k);
    }

    int qsort(vector<int>& nums, int l, int r, int k)
    {
        if(l == r) return nums[l];

        //1.随机选择基准元素
        int key = getRandom(nums, l, r);

        //2.数组分三块
        int i = l, left = l-1, right = r+1;
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left], nums[i++]);
            else if(nums[i] == key) ++i;
            else swap(nums[--right], nums[i]);
        }

        //3.找第k大元素
        int c = r - right + 1, b = right - left - 1;
        if(c >= k) return qsort(nums, right, r, k);
        else if(b + c >= k) return key;
        else return qsort(nums, l, left, k - b -c);
    }

    int getRandom(vector<int>& nums, int left, int right)
    {
        int r = rand();
        return nums[r % (right - left + 1) + left];
    }
};

四、库存管理

LCR 159. 库存管理 III - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof/1.题目解析

求数组中最小的k个数

2.算法分析

法一:排序

法二:优先级队列

法三:快速选择算法

如果我们用快速选择算法对数组分三块之后，求数组中最小的k个数就会快很多

1. a > k, 则最小的k个数都落在黄色区间，递归黄色区间即可

2. a+b>=k, 说明已经找到了前k小的元素，返回即可

3. 递归紫色区间， 注意此时在紫色区间找的是前k-a-b小的元素

3.算法代码

法一:排序

class Solution {
public:
    vector<int> inventoryManagement(vector<int>& stock, int cnt) 
    {
        vector<int> ret;
        sort(stock.begin(), stock.end());
        for(int i = 0; i < cnt; i++)
            ret.push_back(stock[i]);
        return ret;
    }
};

法二:优先级队列

class Solution {
public:
    vector<int> inventoryManagement(vector<int>& stock, int cnt) 
    {
        vector<int> ret;
        priority_queue<int, vector<int>, greater<int>> q; //小堆
        for(auto& e : stock)
            q.push(e);
        while(cnt--)
        {
            ret.push_back(q.top());
            q.pop();   
        }
        return ret;
    }
};

法三:快速选择算法

class Solution 
{
public:
    vector<int> inventoryManagement(vector<int>& nums, int k) 
    {
        srand(time(nullptr));
        qsort(nums, 0, nums.size()-1, k);
        return {nums.begin(), nums.begin() + k};
    }

    void qsort(vector<int>& nums, int l, int r, int k)
    {
        if(l >= r) return;

        //1.选择随机数做key
        int key = getRandom(nums, l, r);

        //2.数组分三块
        int left = l-1, right = r+1, i = l;
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left], nums[i++]);
            else if(nums[i] == key) i++;
            else swap(nums[--right], nums[i]);
        }

        //3.找最小的k个元素
        int a = left - l + 1, b = right - left - 1;
        if(a > k) return qsort(nums, l, left, k);
        else if(a + b >= k) return;
        else return qsort(nums, right, r, k-a-b);
    }

    int getRandom(vector<int>& nums, int l, int r)
    {
        return nums[rand() % (r-l+1) + l];
    }
};

分治-归并

一、排序数组

912. 排序数组 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/sort-an-array/description/1.题目解析

排序数组，升序

2.算法分析

在"分治-快排"中，我们使用快速排序解决了数组升序，这次我们使用归并排序解决问题，选择排序和归并排序都是"分治"思想，可以把"快排"理解成二叉树前序遍历，把"归并"理解成二叉树后序遍历, 详细分析见博客: 排序素来美如玉，层进理解获芳心-CSDN博客

3.算法代码

class Solution {
    vector<int> tmp;
public:
    vector<int> sortArray(vector<int>& nums) 
    {
        tmp.resize(nums.size());
        merge_sort(nums, 0, nums.size()-1);
        return nums;
    }

    void merge_sort(vector<int>& nums, int left, int right)
    {
        //递归结束条件
        if(left >= right) return;

        //1.选择中间节点划分区间
        int mid = (right + left) >> 1;
        //[left, mid], [mid+1, right]

        //2.递归左右区间
        merge_sort(nums, left, mid);
        merge_sort(nums, mid+1, right);

        //3.合并两个有序数组
        //vector<int> tmp(right - left + 1); 在递归过程中，每次都要创建，最好写成全局变量
        int cur1 = left, cur2 = mid + 1, i = 0;
        while(cur1 <= mid && cur2 <= right)
            tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];
        //处理没有遍历完的数组
        while(cur1 <= mid) tmp[i++] = nums[cur1++];
        while(cur2 <= right) tmp[i++] = nums[cur2++];
        //还原
        for(int i = left; i <= right; i++)
            nums[i] = tmp[i - left];
    }
};

二、交易逆序对的总数

LCR 170. 交易逆序对的总数 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/1.题目解析

逆序对是指数对中第一个数>第二个数,  题目要求返回逆序对的个数

2.算法分析
显然可以直接暴力枚举，但是时间复杂度太高，直接超时， 下面是采用归并排序思想解决问题

2.1.将数组划分成两部分，左半部分找一下逆序对，右半部分找一下逆序对，一左一右找一下逆序对，因为本质还是暴力枚举，所以结果一定是正确的

2.2 将数组划分成两部分，左半部分找一下逆序对，然后左半部分排序，右半部分找一下逆序对，然后右半部分排序，一左一右找一下逆序对，结果也是正确的，因为排序并不影响逆序对情况~

由于在左半部分找逆序、右半部分找逆序对以及整个一左一右找逆序对，都属于同一类问题，因此可以用递归求解，而左半部分和右半部分找到逆序对之后都要排序，所以我们在一左一右找完逆序对之后也加一个排序的操作, 分析到这显然就可以用归并排序来求解这道问题了~

下面就是分析左右部分递归完之后，如何一左一右找逆序对的问题了~

策略一: 找出该数之前，有多少数比我大(也就是看左区间内有多少数比nums[cur2]大)

一左一右找逆序对就可以完美的和归并排序中合并两个有序数组完美契合~

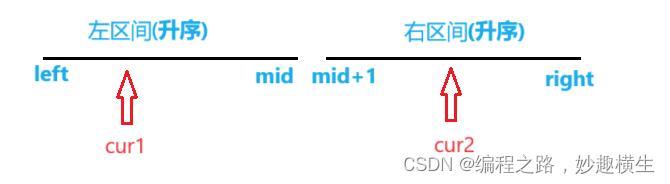
ps: 由合并两个有序数组的逻辑知，哪个指针指向的元素小，就让哪个指针++， 因此[left, cur1-1]区间的所有值都比nums[cur2]小~

①nums[cur1] <= nums[cur2], 说明，对于cur2位置的元素而言，左区间还没有值比nums[cur2]大，没有出现逆序对, 因此继续让cur1++即可

②nums[cur1] > nums[cur2],  而左区间是升序，所以cur1位置之后的所有元素都 > nums[cur2], 此时逆序对的数量 ret += (mid-cur1+1), 然后cur2++来到下一个位置即可

ps:上述合并两个有序数组过程依旧是借助辅助数组来完成的~

注意:该策略数组必须排升序，不能是降序

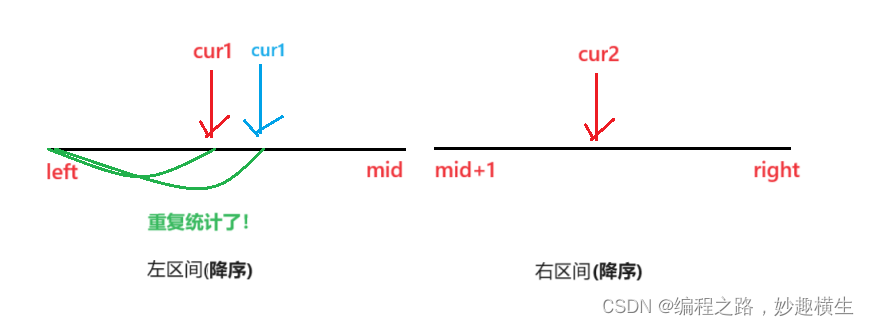
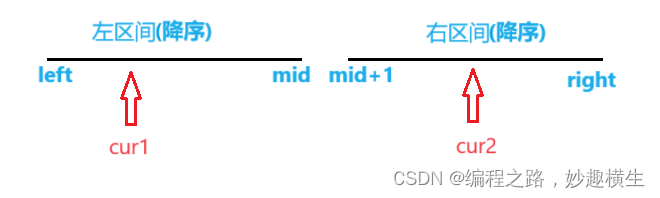
如果是降序，根据归并排序合并两个有序数组，哪个指针指向元素大，哪个指针++， 因此[left, cur1-1]区间的所有值都比nums[cur2]大

此时如果nums[cur1] > nums[cur2], 说明cur1连同cur1之前的左区间元素都比nums[cur2]大， 此时如果统计了逆序对数量，cur1++之后来到下一个位置，此时nums[cur1]依旧可能 > nums[cur2], 还要统计逆序对数量，就会重复计算!!

因此策略一数组只能排升序!

策略二: 找出该数之后，有多少数比我小(也就是看右区间内有多少数比nums[cur1]小)

ps: 由合并两个有序数组的逻辑知 [mid+1, cur2]区间的所有值都比nums[cur1] 大

①nums[cur1] <= nums[cur2], 说明，对于cur1位置的元素而言，右区间还没有值比nums[cur2]小，没有出现逆序对, 因此继续让cur2++即可

②nums[cur1] > nums[cur2],  而右区间是降序，所以cur2位置之后的所有元素都 < nums[cur1], 此时逆序对的数量 ret += (right-cur2+1), 然后cur1++来到下一个位置即可
ps:上述合并两个有序数组过程依旧是借助辅助数组来完成的~

注意:该策略数组必须排降序，不能是升序

如果是升序，根据归并排序合并两个有序数组，哪个指针指向元素小，哪个指针++， 因此[mid+1, cur2]区间的所有值都比nums[cur1]小

如果nums[cur1] > nums[cur2], 说明cur2连同cur2之前的右区间所有元素都比cur1小， 此时如果统计了逆序对数量，cur2++之后来到下一个位置，此时nums[cur1]依旧可能 > nums[cur2], 还要统计逆序对数量，就会重复计算!!

3.算法代码

策略一：

class Solution {
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) 
    {
        return merge_sort(nums, 0, nums.size()-1);
    }

    int merge_sort(vector<int>& nums, int left, int right)
    {
        if(left >= right) return 0;
        int ret = 0; //最终逆序对的数量
        //1.找中间点，将数组分成两部分
        int mid = (left + right) >> 1;

        //2.左边的逆序对个数 + 排序 + 右边的个数 + 排序
        ret += merge_sort(nums, left, mid);
        ret += merge_sort(nums, mid+1, right);

        //3.一左一右的逆序对个数 + 排序
        int cur1 = left, cur2 = mid + 1, i = 0;
        while(cur1 <= mid && cur2 <= right)
        {
            if(nums[cur1] <= nums[cur2])
            {
                tmp[i++] = nums[cur1++];
            }
            else
            {
                ret += mid - cur1 + 1;
                tmp[i++] = nums[cur2++];
            }
        }

        //4.序序的剩余工作
        while(cur1 <= mid) tmp[i++] = nums[cur1++];
        while(cur2 <= right) tmp[i++] = nums[cur2++];
        //还原
        for(int i = left; i <= right; i++)
            nums[i] = tmp[i-left];
        
        return ret;
    }
};

策略二:

class Solution {
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) 
    {
        return merge_sort(nums, 0, nums.size()-1);
    }

    int merge_sort(vector<int>& nums, int left, int right)
    {
        if(left >= right) return 0;
        int ret = 0; //最终逆序对的数量
        //1.找中间点，将数组分成两部分
        int mid = (left + right) >> 1;

        //2.左边的逆序对个数 + 排序 + 右边的个数 + 排序
        ret += merge_sort(nums, left, mid);
        ret += merge_sort(nums, mid+1, right);

        //3.一左一右的逆序对个数 + 排序
        int cur1 = left, cur2 = mid + 1, i = 0;
        while(cur1 <= mid && cur2 <= right)
        {
            if(nums[cur1] <= nums[cur2])
            {
                tmp[i++] = nums[cur2++];
            }
            else
            {
                ret += right - cur2 + 1;
                tmp[i++] = nums[cur1++];
            }
        }

        //4.排序的剩余工作
        while(cur1 <= mid) tmp[i++] = nums[cur1++];
        while(cur2 <= right) tmp[i++] = nums[cur2++];
        //还原
        for(int i = left; i <= right; i++)
            nums[i] = tmp[i-left];
        
        return ret;
    }
};

三、计算右侧小于当前元素的个数

315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/count-of-smaller-numbers-after-self/1.题目解析

本题和题目二求逆序对数量非常相似，不过本题是要返回一个数组，数组的每个元素是原数组元素右侧小于当前元素的个数

2.算法分析

类似题目二，采用归并排序的方法求解

题目二已经详细分析了两种策略，很明显，本题是用策略二，因为本题求的是当前元素以后，有多少个元素比我小, 所以数组应该排降序~

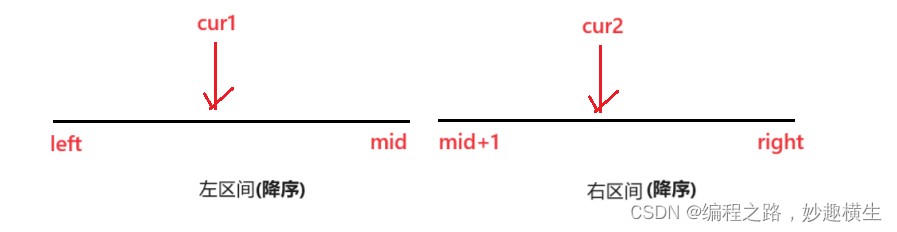
①nums[cur1] <= nums[cur2]：  cur2++

②nums[cur1] > nums[cur2],  由于要返回数组，此时让nums[cu1]元素对应的原始数组下标的位置 的 ret += (right-cur2+1), cur1++

由于处理一左一右的情况是在左右区间都分别排序之后，下标就乱了，所以本题的关键就是要求nums中当前元素的原始下标是多少?

开一个和原始数组大小一样的index数组，将原始数组元素和下标绑定即可~

所以在合并有序数组的时候，nums和index数组都要进行合并，包括后续的还原等工作，都是如此

因此写代码时要有两个辅助数组来解决问题~

3.算法代码

class Solution 
{
    vector<int> ret; //写成全局，不用传成递归参数
    vector<int> index; //记录nums数组当前元素的原始下标
    int tmp_nums[100001]; //辅助数组，用于nums数组中左右两个有序数组的合并
    int tmp_index[100001]; //辅助数组，用于index数组中左右两个有序数组的合并
public:
    vector<int> countSmaller(vector<int>& nums) 
    {
        int n = nums.size();
        ret.resize(n);
        index.resize(n);

        //初始化index数组
        for(int i = 0; i < n; i++)
            index[i] = i;

        merge_sort(nums, 0, nums.size()-1);
        return ret;
    }

    void merge_sort(vector<int>& nums, int left, int right)
    {
        //递归结束
        if(left >= right) return;
        //1.求中间元素下标
        int mid = (left + right) >> 1;
        //[left, mid] [mid+1, right]
        //2.递归左右区间
        merge_sort(nums, left, mid);
        merge_sort(nums, mid+1, right);
        //3.处理一左一右
        int cur1 = left, cur2 = mid + 1, i = 0;
        while(cur1 <= mid && cur2 <= right)
        {
            if(nums[cur1] <= nums[cur2])
            {
                tmp_nums[i] = nums[cur2];
                tmp_index[i++] = index[cur2++];
            }
            else
            {
                ret[index[cur1]] += right-cur2+1;
                tmp_nums[i] = nums[cur1]; 
                tmp_index[i++] = index[cur1++];
            }
        }
        //4.排序的剩余工作
        while(cur1 <= mid) 
        {
            tmp_nums[i] = nums[cur1]; 
            tmp_index[i++] = index[cur1++];
        }
        while(cur2 <= right) 
        {
            tmp_nums[i] = nums[cur2];
            tmp_index[i++] = index[cur2++];
        }
        //还原
        for(int i = left; i <= right; i++)
        {
            nums[i] = tmp_nums[i - left];
            index[i] = tmp_index[i - left];
        }
    }
};

四、翻转对

493. 翻转对 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/reverse-pairs/1.题目解析

翻转对指的是数对中第一个数大于第二个数的两倍,  返回数组中所有翻转对的个数

2.算法分析

首先这道题也是使用分治的思想，整体流程也是将数组划分为两部分，左区间求逆序对数量+排序，右区间求逆序对数量+排序, 然后一左一右求逆序对数量+排序,  但是找翻转对的方法和归并排序中合并两个有序数组并没有完美契合，因为合并两个有序数组判断的是nums[cur1]和nums[cur2]的大小关系，而翻转对要判断的是nums[cur1]与2*nums[cur2]的关系，因此我们可以在合并两个有序数组之前先把翻转对的数量求出来~

策略一:计算当前元素后面，有多少元素的两倍比我小

①nums[cur1] <= 2*nums[cur2], cur2++ 

②nums[cur1]  > 2*nums[cur2], 而数组又是降序，因此cur2位置之后的所有元素的2倍都小于nums[cur1],  ret += right-cur2+1, 然后cur1++

注意情况②cur1++之后，cur2不用回退，因为cur2位置之前的元素的2倍都是大于nums[cur1]的，而数组是降序，cur1++之后，nums[cur1]值更小了，因此cur2回退之后又会一路++到如图位置， 时间复杂度太高了~

策略二:计算当前元素前面，有多少元素的一半比我大

①nums[cur1]  / 2.0  <=  nums[cur2], cur1++ 

②nums[cur1] / 2.0 > nums[cur2], 而数组又是升序，因此cur1位置之后的所有元素的一半都大于nums[cur2],  ret += mid-cur1+1, 然后cur2++

注意情况②cur2++之后，cur1不用回退，因为cur1位置之前的元素的一半都是 <= nums[cur2]的，而数组是升序，cur2++之后，nums[cur2]值更大了，因此cur1回退之后又会一路++到如图位置， 时间复杂度太高了~

3.算法代码

策略一:

class Solution
{
    int tmp[50001];
public:
    int reversePairs(vector<int>& nums) 
    {
        return merge_sort(nums, 0, nums.size()-1);
    }
    int merge_sort(vector<int>& nums, int left, int right)
    {
        int ret = 0;

        //递归结束条件
        if(left >= right) return 0;
        //1.根据中间元素划分区间
        int mid = (left + right) >> 1;
        //2.计算左右区间的翻转对数量
        ret += merge_sort(nums, left, mid);
        ret += merge_sort(nums, mid+1, right);
        //3.计算一左一右翻转对数量
        int cur1 = left, cur2 = mid + 1;
        while(cur1 <= mid)
        {
            while(cur2 <= right && nums[cur1] / 2.0 <= nums[cur2]) //写成 2*nums[cur2] 会超范围
                cur2++;
            if(cur2 > right) break;
            ret += right - cur2 + 1;
            cur1++;
        }
        //4.合并两个有序数组
        cur1 = left, cur2 = mid + 1;
        int i = 0;
        while(cur1 <= mid && cur2 <= right)
            tmp[i++] = nums[cur1] >= nums[cur2] ? nums[cur1++] : nums[cur2++];
        while(cur1 <= mid) tmp[i++] = nums[cur1++];
        while(cur2 <= right) tmp[i++] = nums[cur2++];

        //还原
        for(int i = left; i <= right; i++)
            nums[i] = tmp[i - left];

        return ret;
    }
};

策略二:

class Solution
{
    int tmp[50001];
public:
    int reversePairs(vector<int>& nums) 
    {
        return merge_sort(nums, 0, nums.size()-1);
    }
    int merge_sort(vector<int>& nums, int left, int right)
    {
        int ret = 0;

        //递归结束条件
        if(left >= right) return 0;
        //1.根据中间元素划分区间
        int mid = (left + right) >> 1;
        //2.计算左右区间的翻转对数量
        ret += merge_sort(nums, left, mid);
        ret += merge_sort(nums, mid+1, right);
        //3.计算一左一右翻转对数量
        int cur1 = left, cur2 = mid + 1;
        while(cur2 <= right)
        {
            while(cur1 <= mid && nums[cur1] / 2.0 <= nums[cur2]) //写成 2*nums[cur2] 会超范围
                cur1++;
            if(cur1 > mid) break;
            ret += mid - cur1 + 1;
            cur2++;
        }
        //4.合并两个有序数组
        cur1 = left, cur2 = mid + 1;
        int i = 0;
        while(cur1 <= mid && cur2 <= right)
            tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];
        while(cur1 <= mid) tmp[i++] = nums[cur1++];
        while(cur2 <= right) tmp[i++] = nums[cur2++];

        //还原
        for(int i = left; i <= right; i++)
            nums[i] = tmp[i - left];

        return ret;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1631972.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【bug已解决】发生错误，导致虚拟 CPU 进入关闭状态。如果虚拟机外部发生此错误，则可能已导致物理计算机重新启动......

【bug已解决】发生错误，导致虚拟 CPU 进入关闭状态。如果虚拟机外部发生此错误，则可能已导致物理计算机重新启动......

本bug报错已找到原因，并成功解决。 项目场景： vmware安装ubuntu报错。 如下： 发生错误，导致虚拟 CPU 进入关闭状态。如果虚拟机外部发生此错误，则可能已导致物理计算机重新启动。错误配置虚拟机、客户机操作系统中的错误或 VMware Workstation 中的问题都可以导致关闭状…
阅读更多...
关于google search console工具提交sitemap.xml无法抓取的问题解决办法

关于google search console工具提交sitemap.xml无法抓取的问题解决办法

其实这个问题很好解决。 第一种情况&#xff1a;利用工具为我们的网站自动生成静态的sitemap.xml文件。这种可以检查下是否完整&#xff0c;然后上传到根目录下去&#xff0c;再去google search console提交我们的网站地图。 第二种情况&#xff1a;同样利用工具自动生成动态s…
阅读更多...
idea中使用GlassFish服务器启动项目

idea中使用GlassFish服务器启动项目

idea中使用GlassFish服务器进行测试 1.项目背景 当前在研究openMDM项目, 不过该项目不是springboot项目, 并且是使用GlassFish进行war部署的, 但是需要在idea中进行项目的二次开发,故需要进行idea启动项目并且进行开发和调试 2.GlassFish是什么 GlassFish是一个web服务器, …
阅读更多...
用来传输文件的协议-FTP

用来传输文件的协议-FTP

一.FTP协议--文件传输协议 1.了解FTP协议 &#xff08;1&#xff09;FTP服务是用来传输文件的协议 FTP&#xff08;File Transfer Protocol&#xff0c;文件传输协议&#xff09;是TCP/IP协议组中的协议之一&#xff0c;用于互联网上的控制文件的双向传输。是传输文件到Linu…
阅读更多...
图像置乱加密-Arnold加密算法

图像置乱加密-Arnold加密算法

置乱加密是另一种较常用的加密方法&#xff0c;现也被许多文献选用&#xff0c;置乱加密可以是以像素为单位进行全局置乱&#xff0c;该方式打乱了图像像素值的位置&#xff0c;使其图像内容失去相关性&#xff0c;达到保护的目的。也可以是以块为单位进行置乱&#xff0c;该方…
阅读更多...
软件开发技巧---TODO特殊事项标注

软件开发技巧---TODO特殊事项标注

软件开发技巧—TODO特殊事项标注 文章目录 软件开发技巧---TODO特殊事项标注1、前言2、环境3、TODO注释规范4、Qt中使用TODO5、VS中使用TODO6、总结 更多精彩内容&#x1f449;个人内容分类汇总 &#x1f448;&#x1f449;开发工具 &#x1f448; 1、前言 &#x1f9d8;&…
阅读更多...
头歌：Spark的安装与使用

头歌：Spark的安装与使用

第1关&#xff1a;Scala语言开发环境的部署 相关知识 Scala是一种函数式面向对象语言&#xff0c;它融汇了许多前所未有的特性&#xff0c;而同时又运行于JVM之上。随着开发者对Scala的兴趣日增&#xff0c;以及越来越多的工具支持&#xff0c;无疑Scala语言将成为你手上一件…
阅读更多...
电脑已经有了一个Windows10，再多装一个Windows10组成双系统

电脑已经有了一个Windows10，再多装一个Windows10组成双系统

前言 前段时间已经讲过一次双Windows系统的安装教程&#xff0c;但是小白重新去看了一下&#xff0c;发现写的内容太多&#xff0c;怕小伙伴看了之后一脸萌。 所以今天咱们就重新再来讲讲&#xff1a;在同一台机器上安装Windows10双系统的教程。 注意哦&#xff01;这里的Wi…
阅读更多...
paddlehub的简单应用

paddlehub的简单应用

1、下载安装 pip install paddlehub -i https://pypi.tuna.tsinghua.edu.cn/simple 报错&#xff1a; Collecting onnx<1.9.0 (from paddle2onnx>0.5.1->paddlehub)Using cached https://pypi.tuna.tsinghua.edu.cn/packages/73/e9/5b953497c0e36df589fc60cc6c6b35…
阅读更多...
语音识别的基本概念

语音识别的基本概念

语音识别的基本概念​​​​​​​ ​​​​​​​ 言语是一种复杂的现象。人们很少了解它是如何产生和感知的。天真的想法常常是语音是由单词构成的&#xff0c;而每个单词又由音素组成。不幸的是&#xff0c;现实却大不相同。语音是一个动态过程&#xff0c;没有明确区分的…
阅读更多...
【Unity动画系统】详解Root Motion动画在Unity中的应用（二）

【Unity动画系统】详解Root Motion动画在Unity中的应用（二）

Root Motion遇到Blend Tree 如果Root Motion动画片段的速度是1.8&#xff0c;那么阈值就要设置为1.8&#xff0c;那么在代码中的参数就可以直接反映出Root Motion的最终移动速度。 Compute Thresholds&#xff1a;根据Root Motion中某些数值自动计算这里的阈值。 Velocity X/…
阅读更多...
公共代理IP与独享代理IP的区别是什么？

公共代理IP与独享代理IP的区别是什么？

IP地址&#xff0c;是网络世界中设备互相识别的重要线索&#xff0c;当我们谈论相关话题的时候&#xff0c;总会听说“公共IP”和“独享IP”这两个词。作为用户&#xff0c;我们该如何选择更适合自己的IP资源呢&#xff0c;两者又有何区别&#xff1f; 承载用户量&#xff1a;公…
阅读更多...
ArcGIS小技巧—基于DEM的河网提取

ArcGIS小技巧—基于DEM的河网提取

1、使用DEM数据提取河流水系网络 原始DEM数据中存在误差&#xff0c;或喀斯特地貌等真实地形情况&#xff0c;将引起DEM数据中存在凹陷区域。 在进行水流方向的计算上&#xff0c;如果有洼地会造成错误&#xff0c;因此我们需要进行填洼处理&#xff0c;获得相对准确的DEM数据…
阅读更多...
ULTIMATE VOCAL REMOVER V5 for Mac：专业人声消除软件

ULTIMATE VOCAL REMOVER V5 for Mac：专业人声消除软件

ULTIMATE VOCAL REMOVER V5 for Mac是一款专为Mac用户设计的人声消除软件&#xff0c;它凭借强大的功能和卓越的性能&#xff0c;在音乐制作和后期处理领域崭露头角。 ULTIMATE VOCAL REMOVER V5 for Mac v5.6激活版下载 这款软件基于深度神经网络&#xff0c;通过先进的训练模…
阅读更多...
在美国站群服务器部署时如何保障从253个IP到1000个IP的无缝扩展?

在美国站群服务器部署时如何保障从253个IP到1000个IP的无缝扩展?

在美国站群服务器部署时如何保障从253个IP到1000个IP的无缝扩展? 在当今企业的数字化转型中&#xff0c;服务器的部署和管理成为了保证业务连续性和拓展性的关键。尤其对于站群服务器来说&#xff0c;随着企业业务的增长和市场的扩展&#xff0c;需要从较小规模的253个IP地址…
阅读更多...
Python列表：全面指南

Python列表：全面指南

一、引言 1.1 Python列表简介 在Python编程中&#xff0c;列表&#xff08;List&#xff09;是最常用的数据结构之一&#xff0c;它是一个有序的集合&#xff0c;可以容纳任意类型的对象&#xff0c;如数字、字符串甚至其他列表。列表的特点是可变性&#xff0c;这意味着你可…
阅读更多...
CAPS Wizard for Mac：打字输入辅助应用

CAPS Wizard for Mac：打字输入辅助应用

CAPS Wizard for Mac是一款专为Mac用户设计的打字输入辅助应用&#xff0c;以其简洁、高效的功能&#xff0c;为用户带来了全新的打字体验。 CAPS Wizard for Mac v5.3激活版下载 该软件能够智能预测用户的输入内容&#xff0c;实现快速切换和自动大写锁定&#xff0c;从而大大…
阅读更多...
OK_第6期 | MultiTimer，一款可无限扩展的软件定时器

OK_第6期 | MultiTimer，一款可无限扩展的软件定时器

阅读更多...
看来我对PYTHON的感觉没错，谷歌也已经受不了了

看来我对PYTHON的感觉没错，谷歌也已经受不了了

看来不是我一个人感觉PYHTON不完美了&#xff0c;老东家谷歌已经受不了&#xff0c;直接让走人&#xff01; 你们用Python真的感觉那么好用吗? 你们用Python真的感觉那么好用吗&#xff08;二&#xff09;
阅读更多...
实习面试算法准备之图论

实习面试算法准备之图论

这里写目录标题 1 基础内容1.1 图的表示1.2图的遍历 2 例题2.1 所有可能的路径 1 基础内容 图没啥高深的&#xff0c;本质上就是个高级点的多叉树而已&#xff0c;适用于树的 DFS/BFS 遍历算法&#xff0c;全部适用于图。 1.1 图的表示 图的存储在算法题中常用邻接表和邻接矩…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023