1 基础内容

图没啥高深的，本质上就是个高级点的多叉树而已，适用于树的 DFS/BFS 遍历算法，全部适用于图。

1.1 图的表示

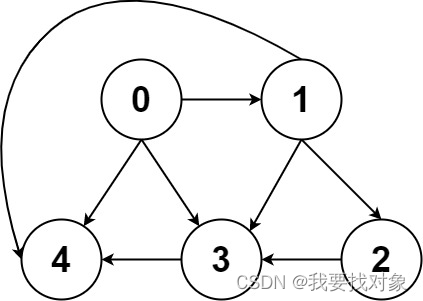
图的存储在算法题中常用邻接表和邻接矩阵表示：

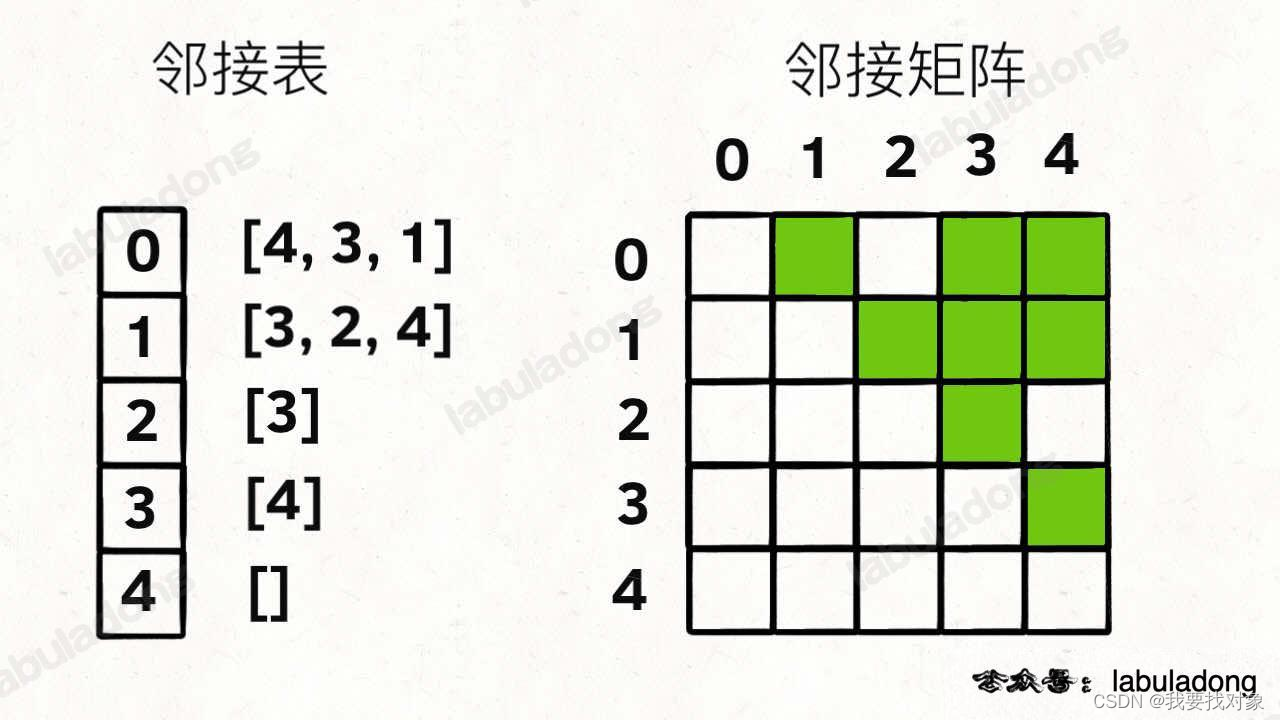
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;

// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;

有向加权图怎么实现？很简单呀：
如果是邻接表，我们不仅仅存储某个节点 x 的所有邻居节点，还存储 x 到每个邻居的权重，不就实现加权有向图了吗？
如果是邻接矩阵，matrix[x][y] 不再是布尔值，而是一个 int 值，0 表示没有连接，其他值表示权重，不就变成加权有向图了吗？
如果用代码的形式来表现，大概长这样：

// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;

// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重，0 表示不相邻
int[][] matrix;

1.2图的遍历

图怎么遍历？还是那句话，参考多叉树，多叉树的 DFS 遍历框架如下：

/* 多叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;
    // 前序位置
    for (TreeNode child : root.children) {
        traverse(child);
    }
    // 后序位置
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点，而树不会出现这种情况，从某个节点出发必然走到叶子节点，绝不可能回到它自身。

所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：

// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

注意 visited 数组和 onPath 数组的区别：
类比贪吃蛇游戏，visited 记录蛇经过过的格子，而 onPath 仅仅记录蛇身。在图的遍历过程中，onPath 用于判断是否成环，类比当贪吃蛇自己咬到自己（成环）的场景。
如果让你处理路径相关的问题，这个 onPath 变量是肯定会被用到的，比如 拓扑排序 中就有运用。
这个 onPath 数组的操作很像前文 回溯算法核心套路 中做「做选择」和「撤销选择」，区别在于位置：回溯算法的「做选择」和「撤销选择」在 for 循环里面，而对 onPath 数组的操作在 for 循环外面。

回忆：
对于回溯算法，我们需要在「树枝」上做选择和撤销选择：

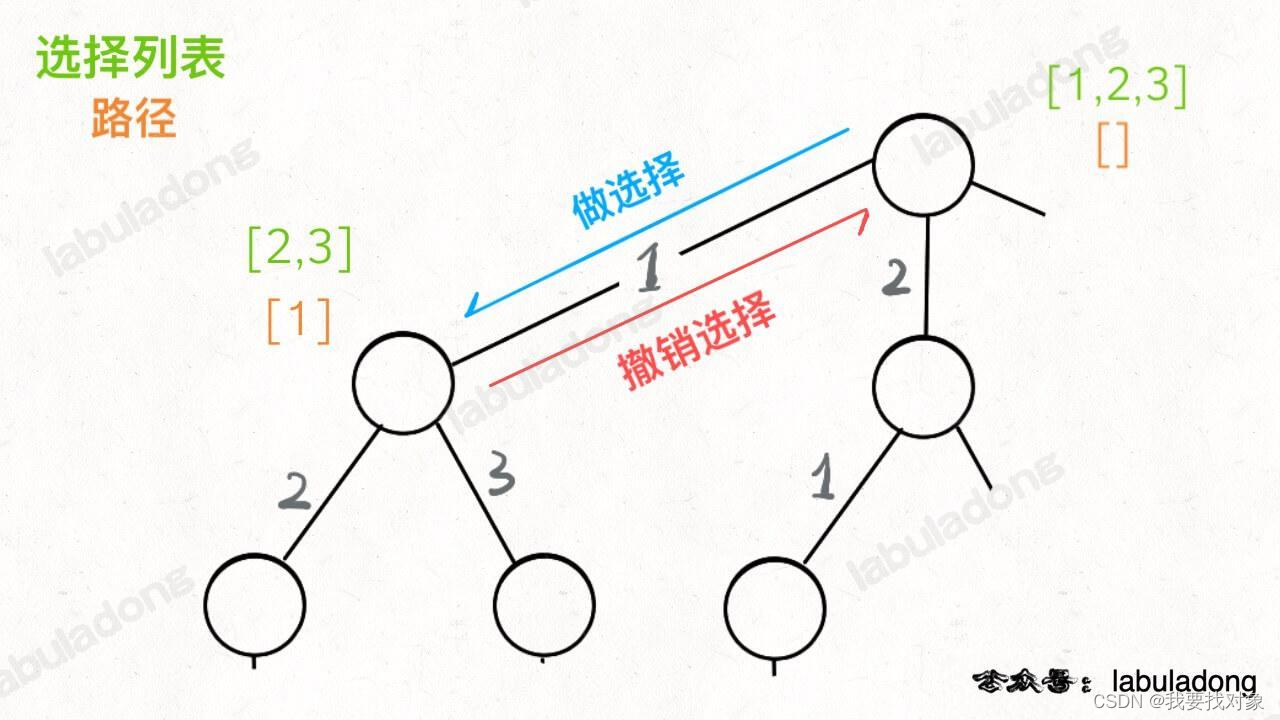
反映到代码上就是：

// DFS 算法，关注点在节点
void traverse(TreeNode root) {
    if (root == null) return;
    printf("进入节点 %s", root);
    for (TreeNode child : root.children) {
        traverse(child);
    }
    printf("离开节点 %s", root);
}

// 回溯算法，关注点在树枝
void backtrack(TreeNode root) {
    if (root == null) return;
    for (TreeNode child : root.children) {
        // 做选择
        printf("从 %s 到 %s", root, child);
        backtrack(child);
        // 撤销选择
        printf("从 %s 到 %s", child, root);
    }
}

另一种解释就是，如果用回溯的方法遍历树，你会发现根节点被漏掉了：

void traverse(TreeNode root) {
    if (root == null) return;
    for (TreeNode child : root.children) {
        printf("进入节点 %s", child);
        traverse(child);
        printf("离开节点 %s", child);
    }
}

所以对于这里「图」的遍历，我们应该用 DFS 算法，即把 onPath 的操作放到 for 循环外面，否则会漏掉记录起始点的遍历。
说了这么多 onPath 数组，再说下 visited 数组，其目的很明显了，由于图可能含有环，visited 数组就是防止递归重复遍历同一个节点进入死循环的。

当然，如果题目告诉你图中不含环，可以把 visited 数组都省掉，基本就是多叉树的遍历。

2 例题

2.1 所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）
graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）

示例1：

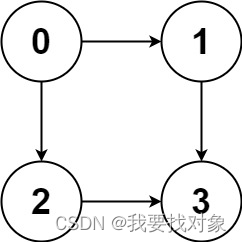
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

代码以及思路：
解法很简单，以 0 为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可。
既然输入的图是无环的，我们就不需要 visited 数组辅助了，直接套用图的遍历框架：

class Solution {
    List<List<Integer>> res = new ArrayList();

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        List<Integer> path = new ArrayList();
        traverse(graph,0,path);
        return res;
    }

    public void traverse(int[][] graph,int s,List<Integer> path){
        path.add(s);
        int n = graph.length;
        if(s == n-1){
            res.add(new ArrayList(path));
        }
        for(int i:graph[s]){
            traverse(graph,i,path);
        }
        path.removeLast();
    }
}