总结不易，还望各位友友，多多支持&&点赞🙏🙏你的鼓励是我更新的动力！！

描述性统计分析是 用几个关键的数字来描述数据集的整体情况 <集中性和离散型（波动性大小）>。

描述数据集常用4个指标： 平均值 四分位数 标准差 标准分
利用这些指标可以进行数据的频数分析、数据的集中趋势分析、数据离散程度分析、数据的分布、以及一些基本的统计图形。

1. 平均值、中位数、众数、极差、四分位数（即下、中、上四份位数）

1️⃣平均值

均值容易受极值的影响，当数据集中出现极值时，所得到的的均值结果将会出现较大的偏差。

2️⃣中位数

数据按照从小到大的顺序排列时，最中间的数据即为中位数。

当数据个数为奇数时，中位数即最中间的数，即位置为（N+1）/2 所对应的值；
当数据个数为偶数时，中位数为中间两个数的平均值

中位数不受极值影响，因此对极值缺乏敏感性。

3️⃣众数

数据中出现次数最多的数字，即频数最大的数值。
众数可能不止一个，众数不仅能用于数值型数据，还可用于非数值型数据，不受极值影响。

4️⃣极差

极差 =最大值-最小值，是描述数据分散程度的量，极差描述了数据的范围，但无法描述其分布状态。
且对异常值敏感，异常值的出现使得数据集的极差有很强的误导性。

5️⃣四分位数（即下、中、上四份位数）

数据从小到大排列，并分成四等份，处于三个分割点位置的数值，即为四分位数。

下四分位数（数据从小到大排列排在第25%位置的数字，即最小的四分位数）、
中间的四分位数即为中位数。
上四分位数（数据从小到大排列排在第75%的数字，即最大的四分位数）、

四分位数可以很容易地识别异常值。（一般通过箱线图表示数据更直观）

在上下边缘之外的数据一般认为是异常值。

---

2. 方差（Var、D(X) 、σ²）、标准差【也叫均方差】（SD 、σ）

1️⃣总体方差 （variance / deviation Var，D(X) ）

定义：是每个样本值与 全体样本值的平均数之差的平方值的平均数

意义：表示数据离散程度。

公式：

实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：将 1/N 换成1/(N-1)


2️⃣总体标准差 （Standard Deviation，SD，σ）

别名：均方差（Mean square error）

定义：是方差的平方根。

意义：由于方差是数据的平方，与检测值本身相差太大，所以常用方差开根号换算回来，这就是我们要说的标准差。

公式：

如是估算样本方差，则将公式中的 1/N 换成1/(N-1)
因为我们大量接触的是样本，所以普遍使用根号内除以（n-1）。

---

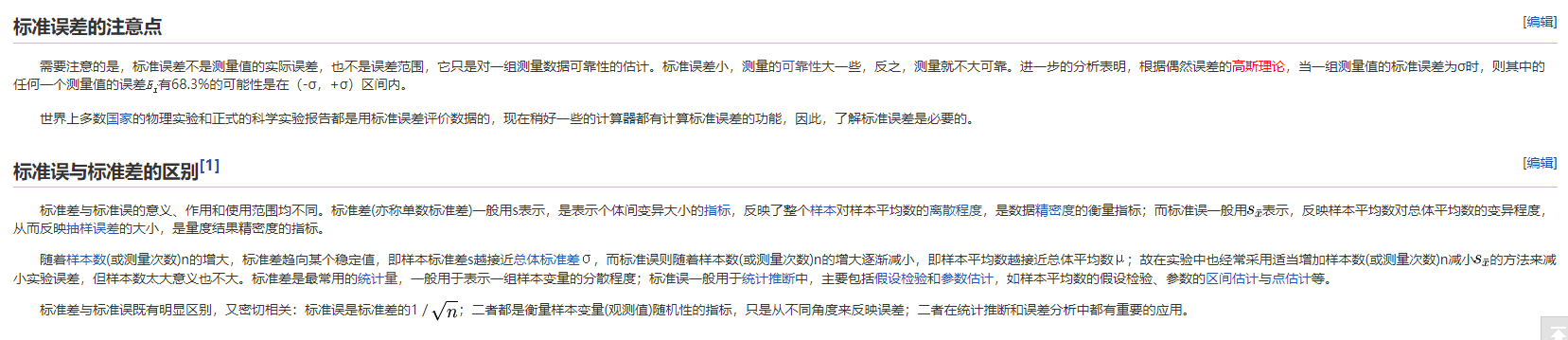
3. 标准误【也叫标准误差、均方根误差】（SE）

标准误差（Standard error），也称均方根误差（Root mean squared error）

标准差与标准误既有明显区别，又密切相关：
标准误是标准差的1/sqrt{n}；二者都是衡量样本变量(观测值)随机性的指标，只是从不同角度来反映误差；

公式：

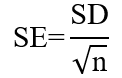
详细见：https://wiki.mbalib.com/wiki/标准误
 

---

4. 标准分

标准分又叫标准差σ的标准化值，每个数据距离平均值多少个标准差。
标准分布又称正态分布。

正态分布中，
至少有68%的数据，位于平均数1个标准差范围内。【即（u-σ ，u+σ）】。
至少有95%的数据，位于平均数2个标准差范围内。【即（u-2σ ，u+2σ）】
至少有99.8%的数据，位于平均数3个标准差范围内。【即（u-3σ ，u+3σ）】

---