题目描述

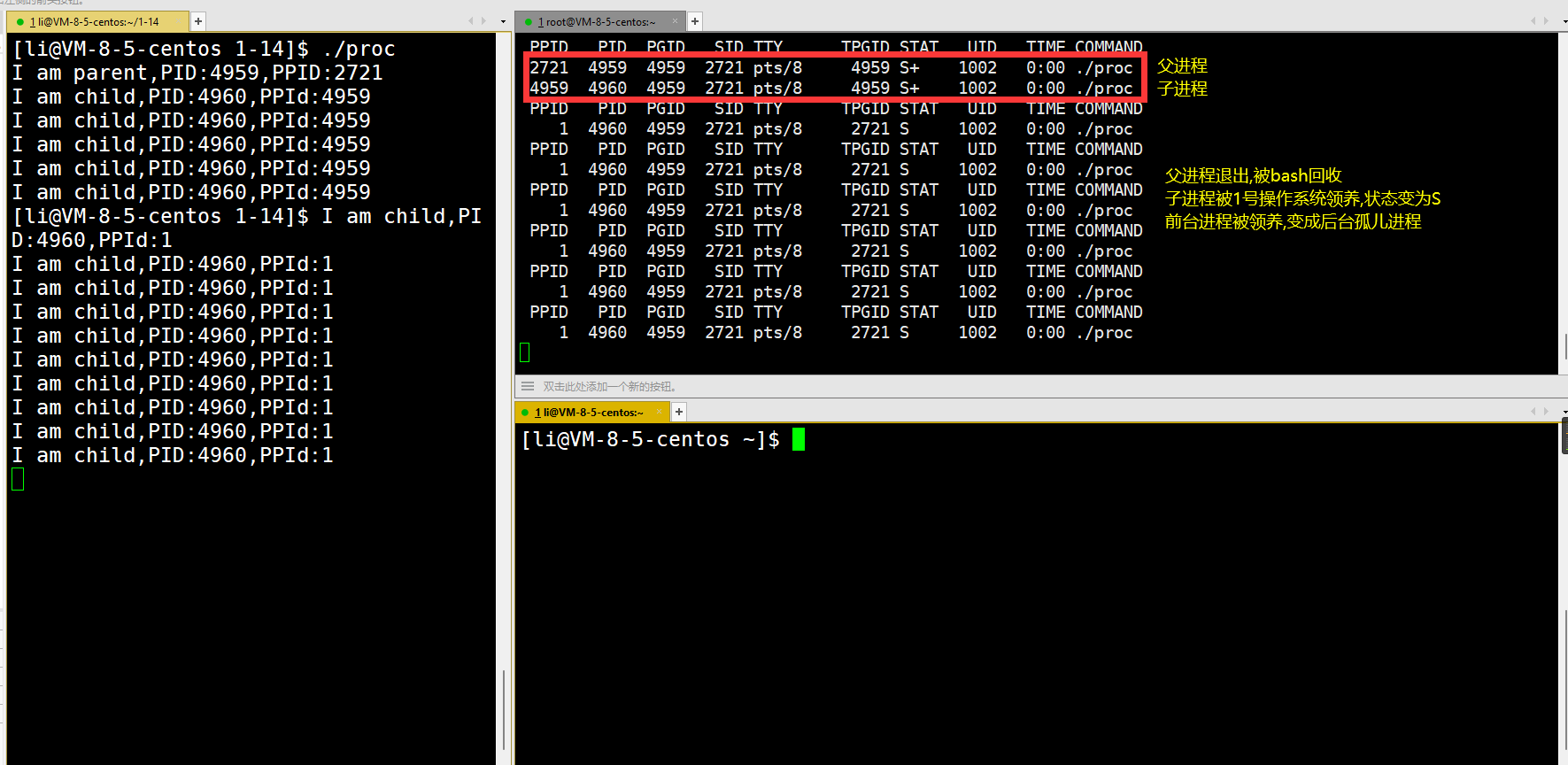
给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从 上到下、从左到右的顺序依次是 A1​,A2​,⋅⋅⋅AN​，如下图所示：

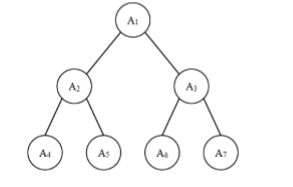
现在小张要把相同深度的节点的权值加在一起，他想知道哪个深度的节点 权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入描述

第一行包含一个整数 N（1≤N≤10^5）。

第二行包含 N 个整数  A1​,A2​,⋅⋅⋅AN​（−10^5 ≤ Ai​ ≤ 10^5）。

输出描述

输出一个整数代表答案。

输入输出样例

输入

7
1 6 5 4 3 2 1

输出

2

参考代码： 

from math import * 
n=int(input())
a=int(log(n,2))+1   #一共有 a 层，log 以 2 为底 n 的对数

s=[0]+list(map(int,input().split())) 
c=[0]*(a+1)  #记录每层的和 c[1]~c[a]
for i in range(1,a+1):   #从第一层到最后一层
  c[i]=sum(s[2**(i-1):2**i-1+1]) #第 i 层和
print(c.index(max(c)))   #查找最大和所在的位置

二叉树的性质：

        每个结点最多有两个子节点：左孩子、右孩子。
        以它们为根的子树称为左子树、右子树。
        二叉树的第 i 层，最多有2-1个节点。
        二叉树的每个节点不必全有左、右孩子，可以只有一个孩子或没有孩子，没有孩子的结点称为叶子节点。

【满二叉树】
        如果每一层的结点数都是满的，称为满二叉树。
【完全二叉树】
        如果满二叉树只在最后一层有缺失，并且缺失的编号都在最后，那么称为完全二叉树。

        例如:满二叉树或完全二叉树，二叉树每一层的结点数量按2的倍数递增，能极快地扩展到很大的范围。一棵有N个结点的满二叉树，树的高度是0(logN)。从根结点到叶子结点，只需要走logN步，例如N=100万，树的高度仅有20，只需要20步就能到达100万个结点中的任意一个。
        二叉树的第 i 层节点最多有2**(i-1)个