1. 概述

在工业界，一个完整的推荐系统中通常包括两个阶段，分别为召回阶段和排序阶段。在召回阶段，根据用户的兴趣从海量的商品中去检索出用户（User）可能感兴趣的候选商品（ Item），满足推荐相关性和多样性需求。在排序阶段，根据不同的目标，如CTR，CVR，时长等对候选出的商品进行打分。目前，对于用户兴趣的建模，通常是从用户的历史行为中挖掘出用户兴趣，以当前的深度学习模型为例，通常是将User的历史行为数据embedding到一个固定长度的向量中，以此表示该用户的兴趣。然而在实际环境中，一个用户的兴趣通常是多样的，使用单一固定长度的embedding向量难以刻画用户兴趣的多样性。Multi-Interest Network with Dynamic routing[1]（MIND）用户多兴趣建模网络取代了原先的单一固定长度embedding向量，取而代之的是用户的多兴趣向量。在MIND中，主要的创新点在于：

1. 通过Mulit-Interest Extractor Layer获取User的多个兴趣向量表达，并采用动态路由（Dynamic Routing）的方法自适应地将User历史行为聚合到User兴趣表达向量中；
2. 通过Label-Aware Attention机制，指导网络学习到用户的多兴趣Embedding向量；

2. 算法原理

2.1. MIND模型的网络结构

MIND模型的网络结构如下图所示：

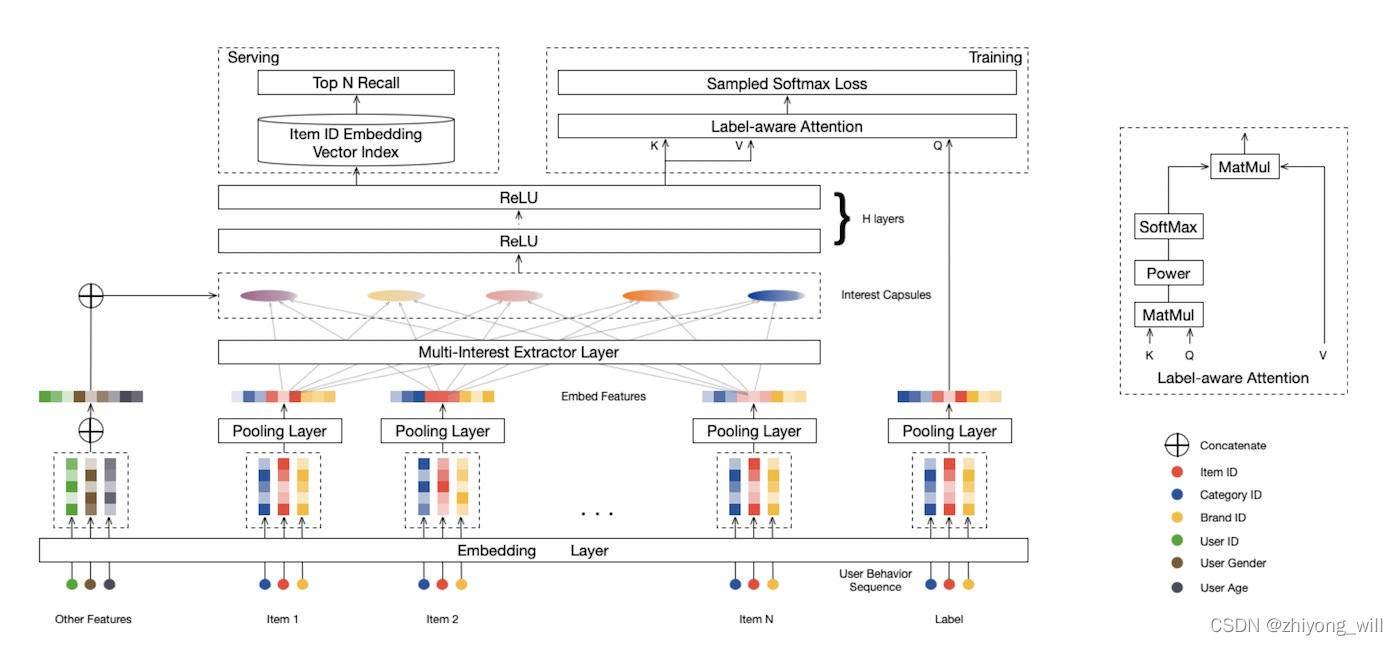
MIND的网络结构与Youtube的召回网络结构[2]基本一致，Youtube的召回网络结构如下图所示：

不同点主要是在多兴趣抽取层Mulit-Interest Extractor Layer和Label-Aware Attention机制。

2.2. Mulit-Interest Extractor Layer

多兴趣抽取层的目的是对用户历史行为的item抽取出多个兴趣向量表达，通常采用聚类的过程将用户的历史行为聚类到多个簇中，一个簇中的item比较靠近，该簇代表了用户兴趣的一个方面。在MIND中，为了实现这样的聚类过程，使用到了胶囊网络（Capsule Network）。

2.2.1. 胶囊网络（Capsule Network）

什么是胶囊网络（Capsule Network）呢？参照参考[3]，对胶囊网络做简单介绍。对于一个普通的神经网络是由神经元组成，每个神经元中是一个具体的值，如下图的左侧图所示；而在胶囊网络中是由被称为Capsule的基本单元组成，与神经元不同的是Capsule中存储的是向量，如下图的右侧图所示。

在上图的胶囊网络中，蓝色的Capsule的输入是黄色的Capsule和绿色的Capsule的输出，分别为向量$v^1$和向量$v^2$，蓝色的Capsule的输出是向量$v$。

2.2.2. 动态路由（Dynamic Routing）

在神经网络中，网络的权重$w_1,w_2,\cdots ,w_n$是在网络的backpropagation过程中学习到的。对于胶囊网络，其过程与神经网络有点不一样，借鉴参考[3]中的图，结合参考[1]中的实例，有如下的图：

假设存在两层的胶囊，当前的第$h$层的胶囊如上图中的蓝色部分，其输入为第$l$层，且上层的输出向量为${\overrightarrow{c}}_i^l\in {\mathbb{R}}^{N_l\times 1}$，且 i ∈ { 1 , ⋯   , m } i\in \left\{1,\cdots ,m \right\} i∈{1,⋯,m}，对应到第$h$层的输出向量为${\overrightarrow{c}}_j^h\in {\mathbb{R}}^{N_h\times 1}$，且 j ∈ { 1 , ⋯   , n } j\in \left\{1,\cdots ,n \right\} j∈{1,⋯,n}，在上图中，我们选取其中一个第$h$层的输出向量${\overrightarrow{c}}_j^h$。${\overrightarrow{z}}_j^h$的计算过程如下：

$${\overrightarrow{z}}_j^h=\sum _{i=1}^m{w}_{ij}{S}_{ij}{\overrightarrow{c}}_i^l$$

其中，矩阵$S_{ij}\in {\mathbb{R}}^{N_h\times N_l}$是需要学习的参数，可通过网络的backpropagation过程学习，连接权重$w_{ij}$在胶囊网络中被称为coupling coefficients，不是在网络中学习得到的。最终通过一个非线性的squash函数得到最终的胶囊的输出向量${\overrightarrow{c}}_j^h$：

$${\overrightarrow{c}}_j^h=squash\left({\overrightarrow{z}}_j^h\right)=\frac{{\Vert {\overrightarrow{z}}_j^h\Vert }^2}{1+{\Vert {\overrightarrow{z}}_j^h\Vert }^2}\frac{{\overrightarrow{z}}_j^h}{\Vert {\overrightarrow{z}}_j^h\Vert }$$

Squash函数的作用是相当于对向量${\overrightarrow{z}}_j^h$做归一化的操作，当至此完成了胶囊网络的前馈过程，然而对于连接权重却并不知道是如何得到的，为了求得连接权重需要使用到动态路由（dynamic routing）的过程，动态路由其实是一个迭代的过程，首先定义the routing logit $b_{ij}$：

$$b_{ij}={\left({\overrightarrow{c}}_j^h\right)}^T{S}_{ij}{\overrightarrow{c}}_i^l$$

那么，$w_{ij}$可以由$b_{ij}$定义：

$$w_{ij}=\frac{exp{b}_{ij}}{{\sum }_{k=1}^{m}exp{b}_{ik}}$$

具体过程如下面的伪代码所示：

2.2.3. 如何理解聚类过程

在参考[4]中详细论述了动态路由与K-Means聚类算法之间的关系，简单来说Capsule所使用的聚类算法，其实是K-Means的变种。通过直观的理解这个过程，首先对于K-Means，为了与上面的Dynamic Routing过程对应，假设原始的样本为$e_i$，其中 i ∈ { 1 , ⋯   , m } i\in \left\{1,\cdots ,m \right\} i∈{1,⋯,m}，存在$K$个聚类中心$u_j$，其中 j ∈ { 1 , ⋯   , K } j\in \left\{1,\cdots ,K \right\} j∈{1,⋯,K}，K-Means的目标是将$m$个原始样本$e_1,e_2,\cdots ,e_m$划分到$K$个类中，使得类内的间隔最小，即：

$$min\sum _{j=1}^K\sum _{i=1}^m{w}_{ij}{\Vert e_i-u_j\Vert }^2$$

其中$w_{i}j$表示样本$e_i$是否属于聚类$j$，因此 w i j ∈ { 0 , 1 } w_{ij}\in \left\{0,1 \right\} wij​∈{0,1}。聚类中心$u_j$为：

$$u_j=\frac{{\sum }_{i=1}^m{w}_{ij}{e}_i}{{\sum }_{i=1}^m{w}_{ij}}$$

与Dynamic Routing中的${\overrightarrow{u}}_j$的更新有两点不一样，第一，计算$w_{ij}$的方式，第二是计算最后结果，在K-Means中是直接求平均，而在Dynamic Routing中，${\overrightarrow{u}}_j$采用的是squash函数。

上述只是从直观上对比了两个过程，具体的数学上的论述可以参见参考[4]。

2.2.4. 动态兴趣个数

对于不同的用户，其兴趣的个数$K$是不一样的，在参考[1]中给出了计算特定用户$u$的兴趣个数$K_u^{{}^{\prime }}$

$$K_u^{{}^{\prime }}=max\left(1,min\left(K,lo{g}_2\left(\left|I_u\right|\right)\right)\right)$$

2.3. Label-aware Attention Layer.

通过多兴趣提取器层，对用户行为序列得到了用户的多个兴趣向量，为了评估多个兴趣向量对目标Item相关度及贡献度，在[1]中设计Label-aware Attention机制来衡量目标Item选择使用哪个兴趣向量，其具体的表达式如下：

$${\overrightarrow{v}}_u=Attention\left({\overrightarrow{e}}_i,V_u,V_u\right)=V_{u}softmax\left(pow\left(V_u^T{\overrightarrow{e}}_i,p\right)\right)$$

其中，$pow$表示的是指数函数，$p$是一个调节attention分布的参数。

3. 总结

在MIND中，通过Mulit-Interest Extractor Layer获取User的多个兴趣向量表达，并采用动态路由（Dynamic Routing）的方法自适应地将User历史行为聚合到User兴趣表达向量中；最后通过Label-Aware Attention机制，指导网络学习到用户的多兴趣Embedding向量。

参考文献

[1] Li C, Liu Z, Wu M, et al. Multi-interest network with dynamic routing for recommendation at Tmall[C]//Proceedings of the 28th ACM international conference on information and knowledge management. 2019: 2615-2623.

[2] Covington P, Adams J, Sargin E. Deep neural networks for youtube recommendations[C]//Proceedings of the 10th ACM conference on recommender systems. 2016: 191-198.

[3] 14.胶囊网络（Capsule Network）

[4] 再来一顿贺岁宴：从K-Means到Capsule

[5]. 推荐系统召回模型之MIND用户多兴趣网络