轮廓系数（Silhouette Coefficient）
轮廓系数用于判断聚类结果的紧密度和分离度。轮廓系数综合了样本与其所属簇内的相似度以及最近的其他簇间的不相似度。
其计算方法如下：
1、计算簇中的每个样本i
1.计算a（i） ：样本i到同簇内其他样本的平均距离，代表样本i的簇内相似度。a（i）的值越小，说明样本i越应该被聚类到该簇，簇内相似度越高。
2.计算b（i）：样本i到其他簇内的所有样本的平均距离的最小值，代表样本i的簇间不相似度。b（i）值越大，说明样本i越不应该被聚类到其他簇。
2、计算轮廓系数

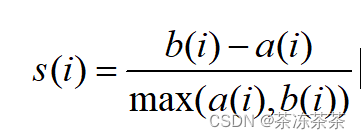
3、轮廓系数分析
轮廓系数的取值范围在[-1,1]之间，系数越大，说明聚类效果越好，簇内相似度越高，簇间差异性越大。

4、Python实现例子

import numpy as np
from scipy.spatial.distance import cdist
data = np.random.rand(1000,10)

def KMeans(X,k,max_iters=100):
    indices = np.random.choice(X.shape[0],k,replace=False)
    centroids = X[indices]
    for _ in range(max_iters):
        distance = np.linalg.norm(X[:,np.newaxis] - centroids,axis=2)
        labels = np.argmin(distance,axis=1)
        new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(k)])
        if np.all(centroids == new_centroids):
            break
        centroids = new_centroids
    return centroids,labels

def silhouette_score(X,label):
    n_samples = X.shape[0]
    silhouette_avg = 0.0
    for i in range(n_samples):
        label = labels[i]
        a = np.mean([cdist(X[i].reshape(1,-1),X[labels == label],'euclidean')[0,1:]])
        b_values = []
        for j in set(labels)-{label}:
            b_values.append(np.min(cdist(X[i].reshape(1,-1),X[labels==j],'euclidean')[0]))
        b = np.mean(b_values)
        s = (b-a)/max(a,b)
        silhouette_avg += s
    silhouette_avg /= n_samples
    
    return silhouette_avg
     
centroids,labels = KMeans(data,10)
silhouette_score(data,labels)