链表相关的题
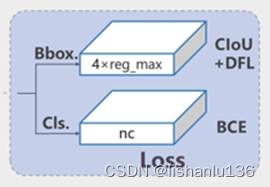
有一个单向链表,链表中有可能出现“环”,如图所示,如何用程序来判断该链表是否为有环链表呢?
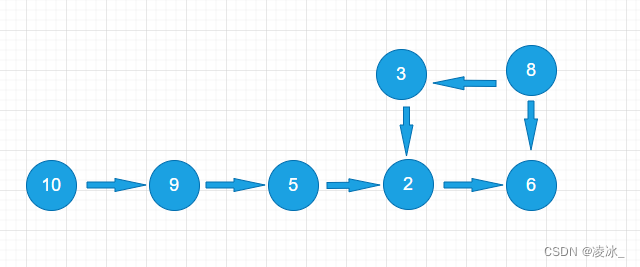
对于这道题,有一个很巧妙的方法,这个方法利用了两个指针。
首先创建两个指针pi和p2(在Python里就是两个对象引用),让它们同时指向这个链表的头节点。然后开始循环,在循环体中,让指针p1每次向后移动1个节点,让指针p2每次向后移动2个节点,然后比较两个指针指向的节点是否相同。如果相同,则可以判断出链表有环,如果不同,则继续下一次循环。
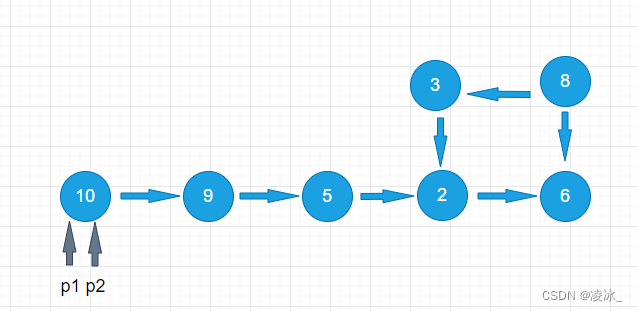
第1步,p1和p2都指向节点10
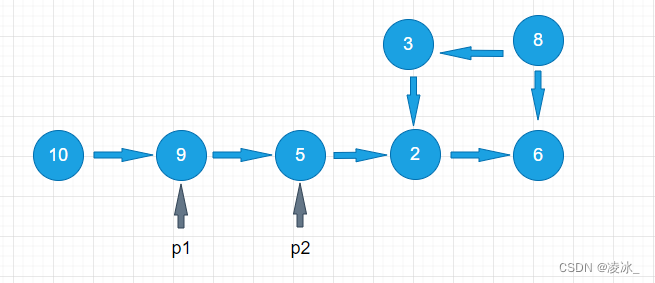
第2步,p1指向节点9,p2指向节点5
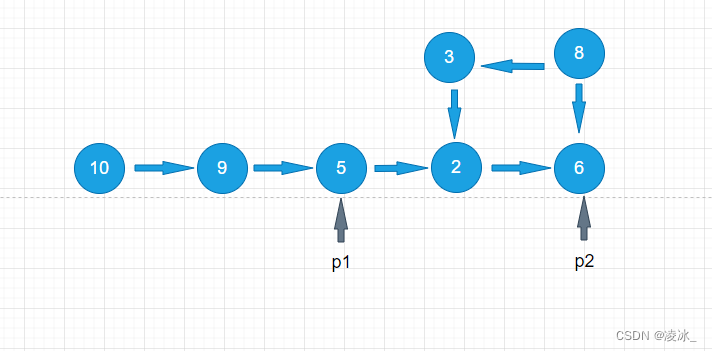
第3步,p1指向节点5,p2指向节点6
第4步,p1指向节点2,p2指向节点3
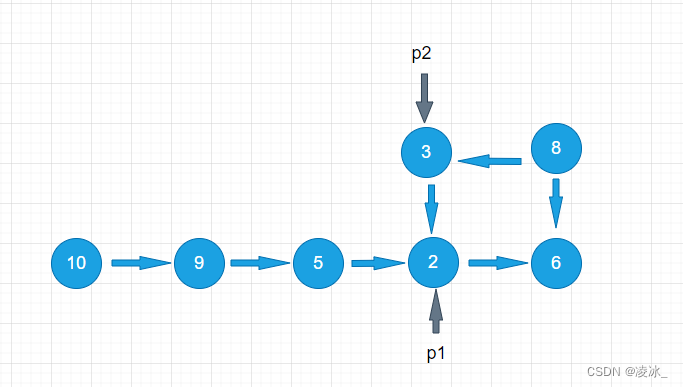
第5步,p1指向节点6,p2也指向节点6,p1和p2所指相同,说明链表有环。
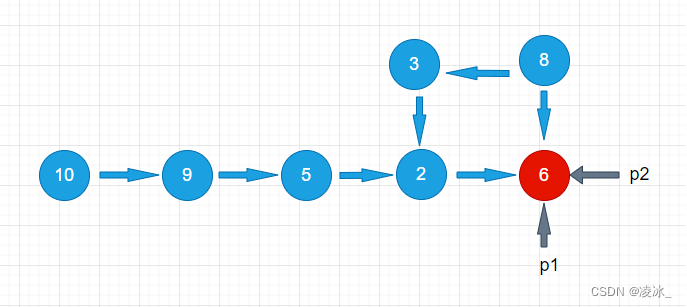
这个题类似于数学上的追及问题。在一个环形跑道上,两个运动员从同一地点起跑,一个运动员速度快,另一个运动员速度慢。当两人跑了一段时间后,速度快的运动员必然会再次追上并超过速度慢的运动员,原因很简单,因为跑道是环形的。
如果链表的节点数量为n,则该算法的时间复杂度为O (n)。除两个指针外,没有使用任何额外的存储空间,所以空间复杂度是O(1)。
class MyNode:
'''初始化节点'''
def __init__(self,data):
self.data=data
self.next=None
def circle_linked(head):
#p1,p2指针指向第一个
p1=p2=head
#循环判断
while p1 is not None and p2.next is not None:
#指针p1每次向后移动1个节点
p1=p1.next
#指针p2每次向后移动2个节点,
p2=p2.next.next
#判断如果相同,返回True
if p1==p2:
return True
return False
if __name__ == '__main__':
#节点数据
n1=MyNode(10)
n2=MyNode(9)
n3=MyNode(5)
n4=MyNode(2)
n5=MyNode(6)
n6=MyNode(8)
n7=MyNode(3)
#链表
n1.next=n2
n2.next=n3
n3.next=n4
n4.next=n5
n5.next=n6
n6.next=n7
n7.next=n4
#调方法
print(circle_linked(n1))
扩展问题1: 如果链表有环,如何求出环的长度?
当两个指针首次相遇,证明链表有环的时候,让两个指针从相遇点继续循环前进,并统计前进的循环次数,直到两个指针第2次相遇。此时,统计出来的前进次数就是环长。
环长=每一次速度差×前进次数
class MyNode:
def __init__(self, data):
self.data = data
self.next = None
def hasCycle(head):
# p1,p2指针指向第一个
p1 = p2 = head
#环长
len = 0
# 循环判断
while p1 is not None and p2.next is not None:
# 指针p1每次向后移动1个节点
p1 = p1.next
# 指针p2每次向后移动2个节点,
p2 = p2.next.next
# 判断如果相遇,就结束循环
if p1 == p2:
break
#循环判断
while (p2 != None) & (p2.next != None):
p1 = p1.next
p2 = p2.next.next
len = len + 1
if p1 == p2:
break
return len
if __name__ == '__main__':
#节点数据
n1=MyNode(10)
n2=MyNode(9)
n3=MyNode(5)
n4=MyNode(2)
n5=MyNode(6)
n6=MyNode(8)
n7=MyNode(3)
#链表
n1.next=n2
n2.next=n3
n3.next=n4
n4.next=n5
n5.next=n6
n6.next=n7
n7.next=n4
#调方法
print(hasCycle(n1))
扩展问题2: 如果链表有环,如何求出入环节点?
抽象示意图:
从链表头节点到入环点的距离是D
从入环点到两个指针首次相遇点的距离是S1
从首次相遇点回到入环点的距离是S2
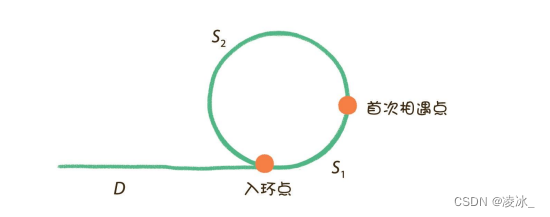
那么,当两个指针首次相遇时,各自所走的距离是多少呢?
指针p1一次只走1步,所走的距离是D+S1。
指针p2一次走2步,多走了n (n>=1)整圈,所走的距离是D+S1+n ( S1+S2)。
由于p2的速度是p1的2倍,所以所走距离也是pi的2倍,因此: 2(D+S1)=D+S1+n(S1+S2)
等式经过整理得出: D=(n-1)(S1+S2)+S2