上节课回顾

上节课的决策边界是通过w，b构建的，因此需通过成本函数，检测逻辑回归模型中的w，b是否为最优解。所以我们首先要直达逻辑回归模型的成本函数。

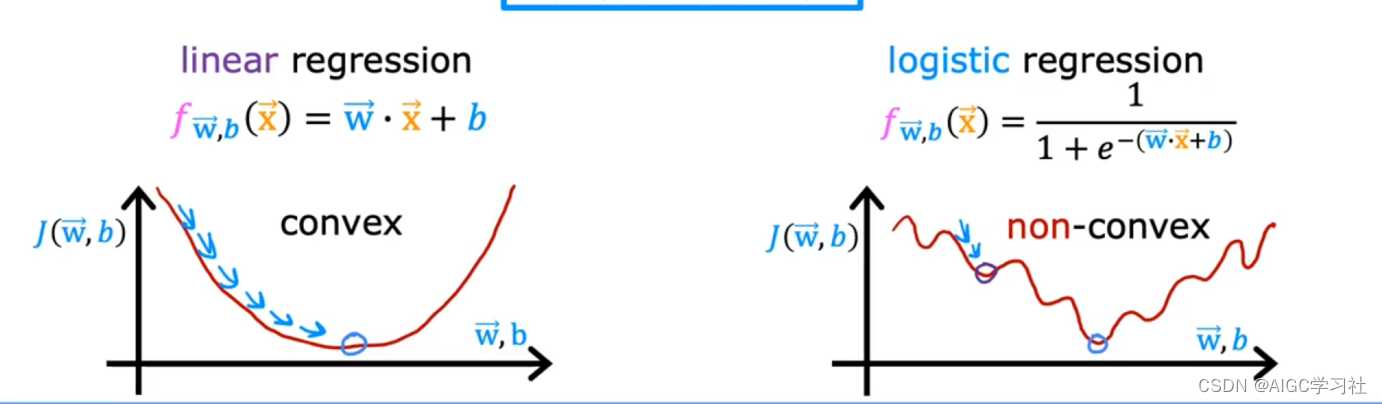
逻辑回归模型使用线性回归模型的平方误差成本函数

如右图所示，如果逻辑回归模型使用平方误差代价函数，则代价函数的值会呈现很多局部最小值，使用梯度下降算法会卡主，梯度下降算法无法找到全局最优解。

单个训练样本的损失

单个训练样本的损失，又叫损失函数，是衡量你在一个训练样本中的表现，也就是某一行训练样本的预测值和真实值的误差的大小。

损失函数，成本函数，代价函数的区别

• 损失函数是衡量单个训练样本的损失，也就是一个样本的预测值与真实值之间的差异。
• 成本函数和代价函数是一个意思，代表每个训练样本的损失的总和。

线性回归损失函数和逻辑回归损失函数的区别

• 线性回归模型的损失函数是计算每组训练样本真实值和预测值的误差平方。
• 逻辑回归模型的成本函数，是用来衡量每组训练样本的预测概率与真实标签之间的接近程度。

逻辑回归模型的成本函数是什么？

使用对数损失函数计算成本函数，不同训练样本的标签对应不同的损失函数。

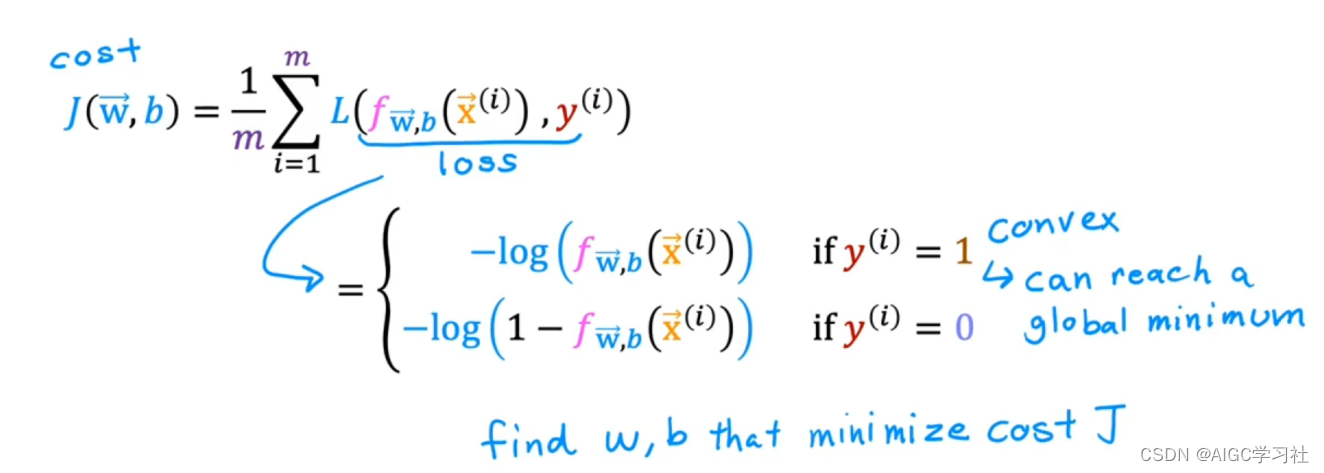
逻辑回归模型的损失函数

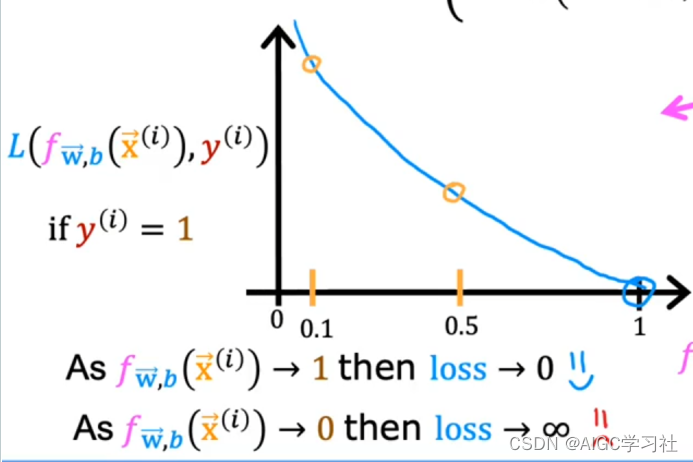
• 当训练样本的真实y=1时，逻辑回归模型的预测f越接近1，代表预测为1的概率越大，损失越小。预测越接近0，代表预测为1的概率小，损失越大。
  
  
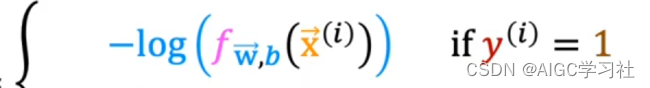
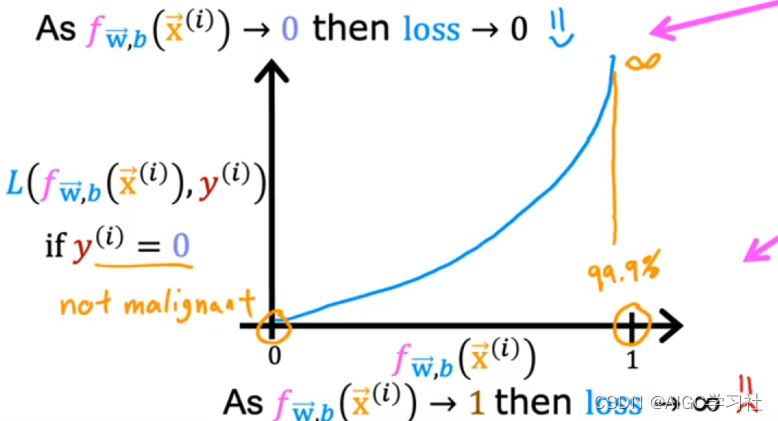
• 当训练样本的真实y=0时，逻辑回归模型的预测f越接近0，代表预测为0的概率越大，损失越小。预测越接近1，代表预测为1的概率越小，损失越大。
  
  

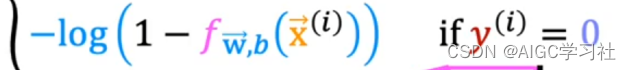
实验

逻辑回归模型使用平方误差成本函数

逻辑回归使用此成本函数，不够平滑，不容易寻找全局最小值。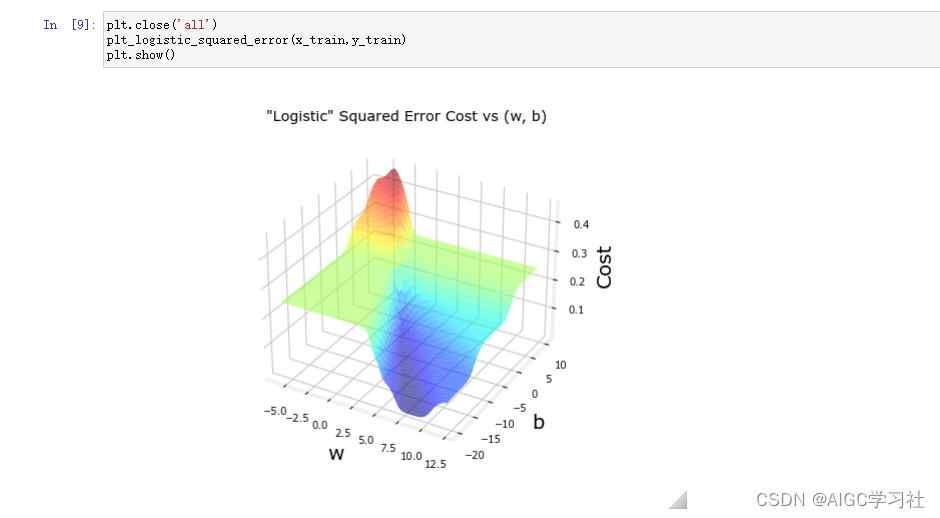

可视化y=1和y=0时的损失函数

逻辑回归模型预测值f和损失值的走势。

逻辑回归模型的损失函数新形式

这个形式不用区分y=1和y=0，计算其中一项时，另一项的结果就会为0。（下节课会细说）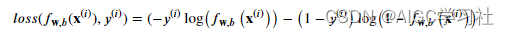

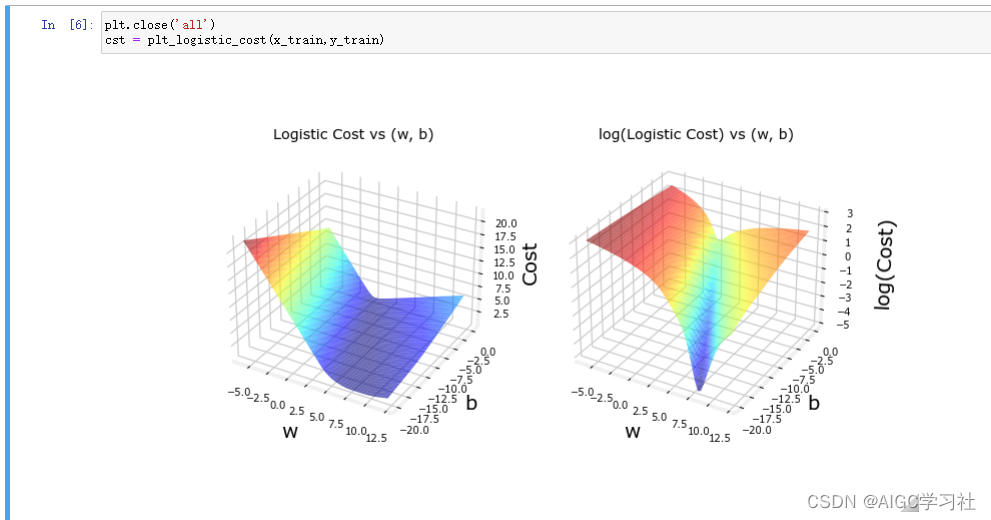
可视化新损失函数的成本函数

新的成本函数以及其对数，对数为了让成本函数的轮廓和最小值（或最低点）更容易辨认。由此看出，逻辑回归模型选择此成本函数，没有高原，不连续，局部最小值。适合梯度下降。

总结

面对分类问题的训练集，需要对数损失函数来衡量每组训练样本的预测值和真实值的差异。差异的具体含义是y=1时，预测y为1的概率的大小。或者y=0时，预测y为0的概率的大小。损失函数是用于衡量单个训练样本，成本函数是衡量整个训练集，也就是累加损失函数的值，然后乘以m/1。如果逻辑回归模型使用平方误差成本函数计算，则成本函数会呈现局部最小值等特点，梯度下降算法可能无法有效地找到全局最优解。