目录
- 1 图
- 2 图的定义和基本概念(在简单图范围内)
- 3 图的类型定义
- 4 图的存储结构
- 4.1 邻接矩阵 表示法
- 4.2 邻接表 表示法
- 4.3 十字链表 表示法
- 4.4 邻接多重表 表示法
- 5 图的遍历
- 5.1 深度优先搜索-DFS 及 广度优先遍历-BFS
- 6 图的应用
- 6.1 最小生成树
- 6.1.1 克鲁斯卡尔 (Kruskal) 算法
- 6.1.2 普里姆 (Prim) 算法算法
- 6.2 最短路径
- 6.2.1 单源点最短路径(Dijkstra算法)
- 6.2.2 单源点最短路径(弗洛伊德算法)
- 6.3 拓扑排序
- 6.4 AOE--网
学习记录,优先理解原理
1 图
图是一种比线性表和树更复杂的数据结构,在线性表中,数据元素之间仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继;在 树形结构中,数据元素之间有着明显的层次关系,并且每一层中的数据元素可能和下一层中的多个元素(即其孩子结点)相关,但只能和上一层中一个元素(即其双亲结点)相关; 而在图结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。数据结构中,则应用图论的知识讨论如何在计算机上实现图的操作,因此主要学习图的存储结构,以及若于图的操作的实现。
2 图的定义和基本概念(在简单图范围内)
图(Graph)是一种数学结构,用于表示对象之间的关系。在图中,通常包含以下元素:一些简单的概念术语就不讨论了,例如:
提醒一点下图是一个图还是4个图?(一个图,千万别说成四个图)

- (x,y)指由x点到y点,且无方向;也就是(x,y)=(y,x);
- <x,y>指由x到y,但是有方向;也就是<x,y>!=<y,x>;
- 什么是顶点?
- 什么是边?
- 什么是图?
- 什么是子图? —就是从一个图中拿走一部分,这部分就是子图,隶属关系
- 什么是有向图?—只要有一根线带方向就是有向图
- 什么是完全有向图?—就是图的所有线都有方向
(n个顶点就是有${n(n-1)}$条线都有方向) - 什么是无向图?—就是没有一根线带方向
- 什么是完全无向图?—就是图的所有线都没有方向
(n个顶点就是有${n(n-1)/2}$条线都无方向) - 所以思考一个问题:a,b两个点,如果是无向图,最多是1条线,如果有向图是两条线:很重要:如下图,所以n个顶点,有向图最多n(n-1)条线,无向图最多是有向的一半;

- 什么是权?—就是一条线的价值(数值)
- 什么是邻接点?—无向图中挨着的点就是邻接点;
但是注意在有向图中:如果 A 指向 B,但 B 不指向 A,那么 B 的邻接点是 A,A的邻接点不是B - 什么是度?—针对无向图,就是一根节点被插了几条线,注意无向图没有方向;出==入
- 什么是入度?出度?—针对有向图,就是一个点射出几条线为出度,插入几条线就是入度;
以上就是一些基本的简单的概念,稍微理解一下就行,下面的就有一些抽象,可以讨论一下
- 回路或者环;如下图画出来的就是环,第一个顶点和最后一个顶点相同的路径称为回路或环

- 连通、连通分量、连通图;
这些针对无向图,首先是连通,连通的意思就是两个节点之间有线,如下图,V1到V2,V1到V5 都叫连通,画线都叫连通:

知道了连通的意思,那么连通图的意思就是很好理解了,连通图顾名思义任意两个顶点都能连通。
现在再问一下,下面的是一个图还是三个图,是连通图吗?----一个图----不是连通图

很多人第一印象就是觉得是三个图,其实不然,图是一个集合,所以是一个图,这些集合中的元素如何区分呢?我们利用连通分量的的概念就能进行区分,连通分量指的是无向图中的极大连通子图,上图中刚好有三个连通分量(每个连通分量都是一个极大连通子图);如下:

这样就能分成三个好研究的子图;即-连通分量指的是无向图中的极大连通子图
- 我们上面谈完无向图中叫连通、连通图、连通分量,那么在有向图中怎么叫呢?我觉得叫有向连通,比较通俗易懂,但是学术名称是强连通图和强连通分量:在有向图 G 中,如果对千每一对Vi,Vj属于 V;从 Vj到Vi都存在路径,则称G是强连通图。有向图中的极大强连通子图称作有向图的强连通分量。例如下图,不是强连通图,但它有两个强连通分量,如图:

- 剩下两个概念就是连通图的生成树和有向树和生成森林:
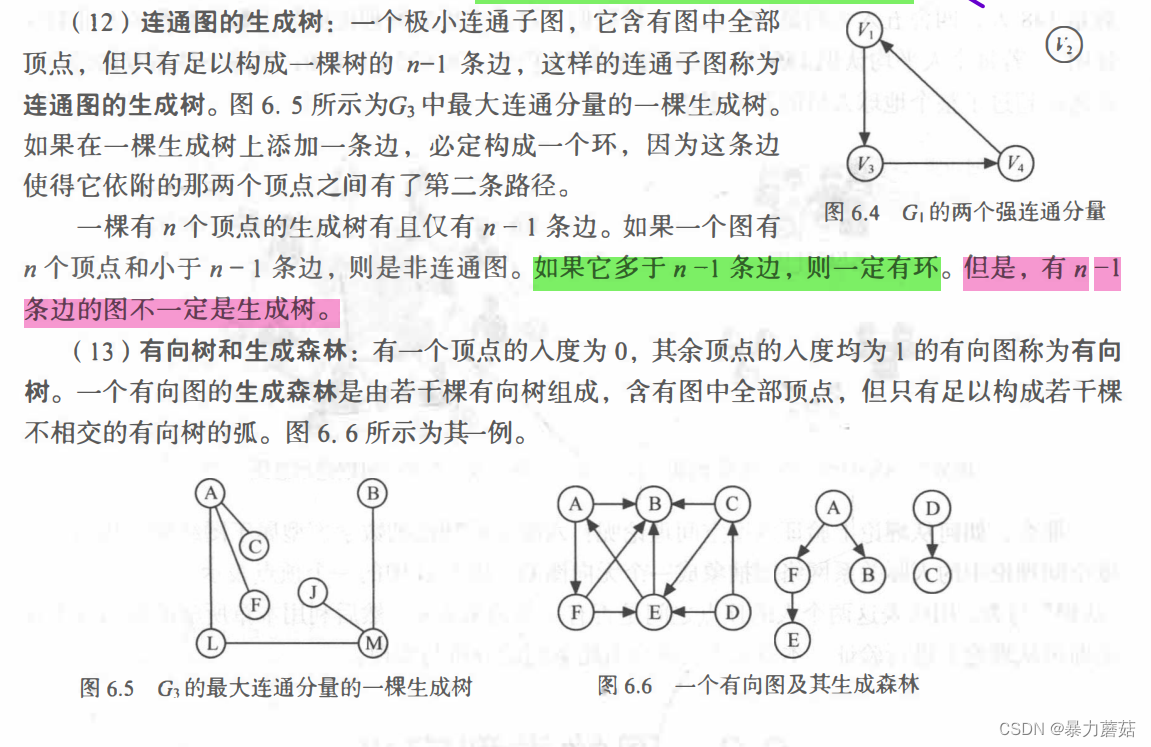
3 图的类型定义
图是一种数据结构,加上一组基本操作,就构成了抽象数据类型。抽象数据类型图的定义如下;还记得之前对于复数的抽象数据类型的定义吗:如下:三部分-数据对象,数据关系,基本操作;

依次类比关于图的抽象数据结构如下:

基本操作还有很多,这个可以根据自己的需求进行一些基本操作的编写;
4 图的存储结构
由千图的结构比较复杂,任意两个顶点之间都可能存在联系,因此无法以数据元素在存储区中的物理位置来表示元素之间的关系,即图没有顺序存储结构,但可以借助二维数组来表示元素之间的关系,即邻接矩阵表示法。另一方面,由千图的任意两个顶点间都可能存在关系,因此,用链式存储表示图是很自然的事,图的链式存储有多种,有邻接表、十字链表和邻接多重表,应根据实际需要的不同选择不同的存储结构。
4.1 邻接矩阵 表示法
邻接表示法如下图所示:

除了一个用千存储邻接矩阵的二维数组外, 还需要用一个一维数组来存储顶点信息。 创建一个采用邻接矩阵表示法创建无向网:
 这样的存储方式有缺点也有优点,缺点就是矩阵的通病,对于稀疏的图,这样会造成大量的空间浪费;
这样的存储方式有缺点也有优点,缺点就是矩阵的通病,对于稀疏的图,这样会造成大量的空间浪费;
4.2 邻接表 表示法
表头是一个数组结构体指针,每个结构体指针指向一个链表,有如下图:
在邻接表中,对图中每个顶点V; 建立一个单链表,把与 V相邻接的顶点放在这个链表中,邻接表中每个单链表的第一个结点存放有关顶。

值得注意的是,一个图的邻接矩阵表示是唯一的,但其邻接表表示不唯一,这是因为邻接表表示中,各边表结点的链接次序取决于建立邻接表的算法,以及边的输入次序。
4.3 十字链表 表示法
十字链表(Orthogonal List)是有向图的另一种链式存储结构,可以看成将有向图的正邻接表和逆邻接表结合起来得到的一种链表。在十字链接结构中,对应于每个顶点有一个结点,对应于有向图中每一条弧也有一个结点,每条弧的弧头结点和弧尾结点都存放在链表中。
十字链表是为了便于求得图中顶点的度(出度和入度)而提出来的,它是综合邻接表和逆邻接表形式的一种链式存储结构。在十字链表存储结构中,有向图中的顶点的结构如下所示:
data:表示顶点的具体数据信息。firstIn:指向以该顶点为弧头的第一个弧节点。firstOut:指向以该顶点为弧尾的第一个弧节点。
为了表示有向图中所有的顶点,采用一个顶点数组存储每一个结点。弧节点是十字链表存储结构中用于表示有向图中每一条弧的节点。它的结构包含以下几个域:tailVex:表示该弧的弧尾顶点在顶点数组中的位置。headVex:表示该弧的弧头顶点在顶点数组中的位置。nextArc:指向弧头相同的下一条弧。prevArc:指向弧尾相同的下一条弧。info:该弧的信息。
弧节点通过tailVex和headVex字段与顶点节点相连,形成了有向图的存储结构。通过弧节点的链接关系,可以方便地访问有向图中的弧信息,以及进行与弧相关的操作,如遍历弧、查找弧等。

4.4 邻接多重表 表示法
待补充、、、、、
5 图的遍历
和树的遍历类似,图的遍历也是从图的某一项点开始,按照某种方法对图中所有顶点访问且仅访问一次。图的遍历算法是求解图的连通性问题,拓扑排序和关键路径等算法的基础。
5.1 深度优先搜索-DFS 及 广度优先遍历-BFS
理解这个之前,先理解一下树中的DFS和BFS遍历,其实树中的DFS就是后序遍历,BFS就是层次遍历,如下图:

现在放到图中,依然是这样,对于图而言,DFS就是一直找到头,到头后开始访问,就类似于树中的后序访问(其中最重要的是回溯的思想),而BFS就是广度优先遍历,要用到队列,核心就是一层一层的进行遍历:如下图:和深度优先搜索类似,广度优先搜索在遍历的过程中也需要一个访问标志数组。回退时判断有没有访问过这个节点

6 图的应用
6.1 最小生成树
先明白一个问题就是,最小生成树是一颗树,树的各个点都是连通的,N个节点的树有n-1根线,拿无向图而言,而对于一个图而言,其可能是由很多连通图组成的一个大图,但是要组成一棵树,就不能有环的存在,而且整个图是连通的,且其线是n-1条,这样才能生成一颗树,其中每条线对应一个数值,把这些数值相加得到一个整体的值这个值如果最小,那么就是得到了最小的生成树;采用贪婪算法,主要的算法有:克鲁斯卡尔 (Kruskal) 算法和普里姆 (Prim) 算法。
6.1.1 克鲁斯卡尔 (Kruskal) 算法
这个算法的步骤就是,先把所有的边存储起来,然后把边从小到大进行排序,然后依次把边从小到大放回原图,也称为加边法,并每次进行判断有没有环的生成,如果又环的生成,就放弃这条线,再向下面取线,直到取到n-1条线,就生成了最小生成树。
与普里姆算法相比,克鲁斯卡尔算法更适合千求稀疏网的最小生成树

6.1.2 普里姆 (Prim) 算法算法
这个算法有点抽象,核心就是找两个集合之间的最短路径,其中一个集合就是已找到的节点,另外一个集合就是未找到的节点集合,找出中间最短的路径,并纳入一个新的节点,也称 加点法,核心原理就是这样,不用判断有没有环:注意:每次选择最小边时, 可能存在多条同样权值的边可选, 此时任选其一即可。
普里姆算法的时间复杂度为 O(n^2), 与网中的边数无关, 因此适用千求稠密网的最小生成树。

6.2 最短路径
假设一个人不考虑费用和时间,从A到B,要求中转次数最少,那么这就是一个简单图的问题,简化一下,就是求A到B的最短路径,可以采用图的层次遍历也就是BFS算法(广度优先搜索),直到遇到顶点B就停止,其中中转次数就是A到B之间的节点数;
显然问题还可以进一步的深入,对于旅客而言,他们关心的就是A到B的费用最少,而对于司机而言,他们更关心的是里程和速度,因此要对图中进行一些改变:为了在图上表示有关信息,可对边赋以权,权的值表示两城市间的距离,或途中所需时间,或交通费用等。此时路径长度的度最就不再是路径上边的数目,而是路径上边的权值之和。考虑到交通图的有向性,例如,汽车的上山和下山,轮船的顺水和逆水,所花费的时间或代价就不相同,所以交通网往往是用带权有向网表示。在带权有向网中,习惯上称路径上的第一个顶点为源点(Source), 最后一个顶点为终点(Destination);

6.2.1 单源点最短路径(Dijkstra算法)
本节将讨论单源点的最短路径问题:给定带权有向图G和源点Vo , 求从Vo到G中其余各顶点的最短路径。迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径的算法,
称为迪杰斯特拉算法。
注意最小生成树不等于Dijkstra算法:两个解决的问题不一样, 一个是求最短的路线, 一个是解决怎么花最小的成本连通所有点不过Dijkstra算法和最小生成树里的Prim算法思路还挺像的, 但要注意Dijkstra算法每次找的是距离源点(比如我视频里的a点)最近的点, 但是Prim算法每次找的是距离正在生成的树最近的点. 有的点可能距离正在生成的树是最近的但是距离源点不是最近的, 所以Dijkstra算法不等于Prim算法, 也不能用来求最小生成树。

6.2.2 单源点最短路径(弗洛伊德算法)
待补充
6.3 拓扑排序
一个无环的有向图称作有向无环图( DirectedAcycline Graph), 简称DAG图。有向无环图是描述一项工程或系统的进行过程的有效工具。通常把计划、 施工过程、 生产流程、 程序流程等都当成一个工程。除了很小的工程外,一般的工程都可分为若干个称做活动(Activity)的子工程,而这些子工程之间, 通常受着一定条件的约束, 如其中某些子工程的开始必须在另一些子工程完成之后。
待补充–
6.4 AOE–网
与AOV-网相对应的是AOE-网 (Activity On Edge) , 即以边表示活动的网。 AOE-网是一个带权的有向无环图, 其中, 顶点表示事件, 弧表示活动, 权表示活动持续的时间。 通常, AOE-网可用来估算工程的完成时间。
待补充–