题目列表

3120. 统计特殊字母的数量 I

3121. 统计特殊字母的数量 II

3122. 使矩阵满足条件的最少操作次数

3123. 最短路径中的边

一、统计特殊字母的数量I

分别统计小写字母和大写字母是否出现，然后求交集即可，这里我们可以用数组统计，但其实没必要，一共就26个字母，我们可以用26个bit位的0/1来表示字符是否存在，由于区分大小写，所以我们共需要两个int变量就行，代码如下

class Solution {
public:
    int numberOfSpecialChars(string word) {
        int cnt[2]={0};
        for(auto e:word){
            if((e>>5)&1) cnt[0] |= 1<<(e-'a'); // 小写字母的二进制表示的第5位为1，大写字母为0
            else cnt[1] |= 1<<(e-'A');
        }
        return __builtin_popcount(cnt[0]&cnt[1]);
    }
};

二、统计特殊字母的数量II

 

这题和第一题的区别是限定了大小写字母的位置关系，即小写字母必须在其对应的大写字母的前面，这个其实也很容易，我们只要统计不同小写字母出现的最靠后的位置和不同大写字母出现的最靠前的位置，来看对应的大小写字母是否符合条件即可，代码如下

class Solution {
public:
    int numberOfSpecialChars(string word) {
        int n = word.size();
        vector<int>first(26,-1);//记录大写字母出现最靠前的位置
        vector<int>last(26,-1);//记录小写字母出现最靠后的位置
        for(int i=0;i<n;i++){
            char c = word[i];
            if((c>>5)&1) last[c-'a']=i;
            else {
                if(first[c-'A']==-1) 
                    first[c-'A']=i;
            }
        }
        int ans = 0;
        for(int i=0;i<26;i++){
            if(first[i]<0||last[i]<0) continue;
            ans += first[i]>last[i];
        }
        return ans;
    }
};

能不能改为一次遍历呢？？？实际上是否满足条件符合下面这样一个状态转换关系

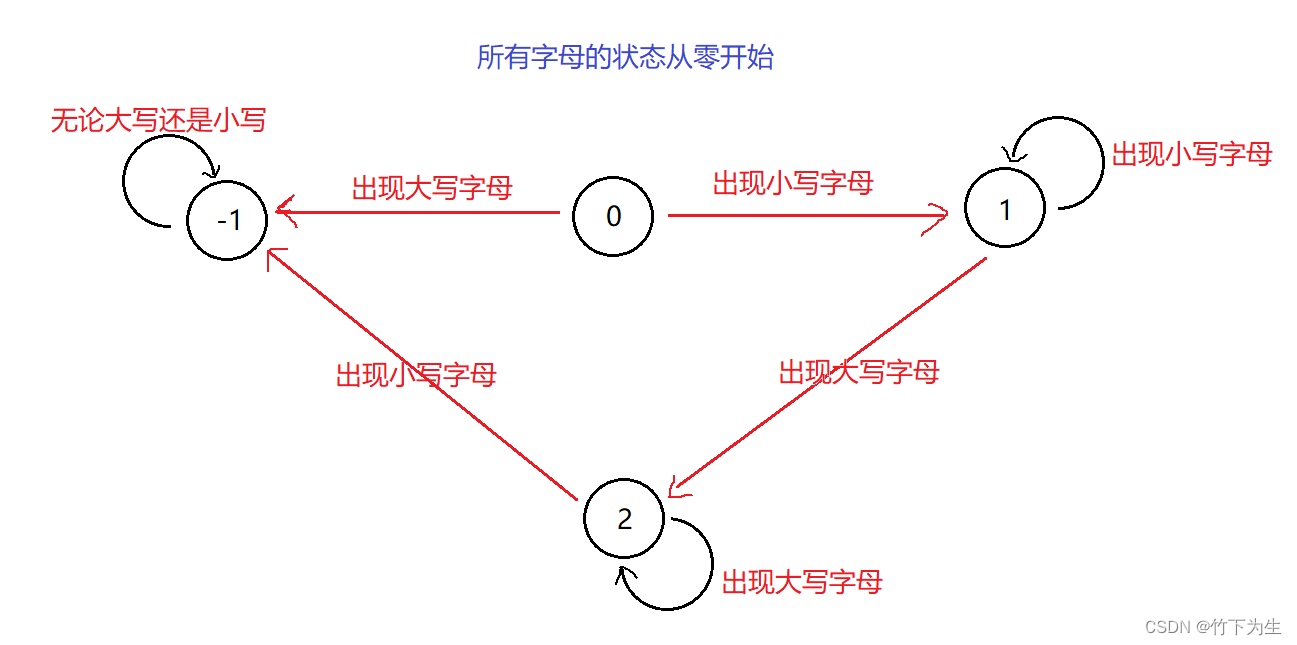
代码如下

class Solution {
public:
    int numberOfSpecialChars(string word) {
        int n = word.size(),cnt = 0;
        vector<int>status(26);
        for(auto e:word){ // 边进行状态转化，边统计符合条件的字母个数
            if((e>>5)&1){
                int i = e - 'a';
                if(status[i]==0) status[i]=1;
                else if(status[i]==2) status[i]=-1,cnt--;
            }else{
                int i = e - 'A';
                if(status[i]==0) status[i]=-1;
                else if(status[i]==1) status[i]=2,cnt++;
            }
        }
        return cnt;
    }
};

三、使矩阵满足条件的最少操作次数

根据题目条件， 我们知道符合条件的矩阵满足，每一列的元素都相同且相邻列的元素不同，也就是说，我们只关心每一列的元素情况，所以我们可以先统计每一列中的0-9出现的次数。题目要求最少操作次数，也就是我们最多能让多少个元素保持不变，由此我们设计出如下的状态定义：

f[i][j]表示前i列中，第i列元素为j时，最多能有多少个元素保持不变

状态转移方程：f[i+1][j] = max(f[i][k])+cnt[i][j]，0<=k<=9&&k!=j

初始化：f[0][j] = 0，前0列没有元素，最多保留0个元素不变

代码如下

class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> cnt(m,vector<int>(10));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                cnt[i][grid[j][i]]++;
            }
        }
        vector<vector<int>> dp(m+1,vector<int>(10));
        // dp[i][j] 表示当前位置为j且前i列符合条件的不需要改变的最大元素个数
        // dp[i][j] = max(dp[i-1][k]) + cnt[i][j] k!=j 0-9
        for(int i=0;i<m;i++){
            for(int j=0;j<10;j++){
                int mx = INT_MIN;
                for(int k=0;k<10;k++){
                    if(k==j) continue;
                    mx = max(mx,dp[i][k]);
                }
                dp[i+1][j]=mx + cnt[i][j];
            }
        }
        return n*m-*max_element(dp.back().begin(),dp.back().end());
    }
};

// 空间优化
class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> cnt(m,vector<int>(10));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                cnt[i][grid[j][i]]++;
            }
        }
        vector<int>f(10);
        for(int i=0;i<m;i++){
            vector<int>tmp(10);
            for(int j=0;j<10;j++){
                int mx = INT_MIN;
                for(int k=0;k<10;k++){
                    if(k==j) continue;
                    mx = max(mx,f[k]);
                }
                tmp[j]=mx + cnt[i][j];
            }
            f=tmp;
        }
        return n*m-*max_element(f.begin(),f.end());
    }
};

通过上述的状态定义，我们知道这题本质就是在求当前选择0-9中的几时，保留下来的数最多，由于相邻的列元素不同这一条件，其实我们只要维护前i-1列中保留下来的数的最大值和次大值即可，只有这两个值才会对第i列的状态最值产生影响【类似于我们如果只求数组中的最大值，就没必要将整个数组排序，只要遍历一边即可】，代码如下

class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> cnt(m,vector<int>(10));
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                cnt[i][grid[j][i]]++;
            }
        }
        int f0 = 0, f1 = 0;
        int pre = -1;
        for(int i=0;i<m;i++){
            int mx = 0, mx2 = 0, x;
            for(int j=0;j<10;j++){
                int res = (j==pre?f1:f0) + cnt[i][j];
                if(res > mx) mx2 = mx, mx = res, x = j;
                else if(res > mx2) mx2 = res;
            }
            f0 = mx, f1 = mx2, pre = x;
        }
        return n*m-f0;
    }
};

四、最短路径中的边

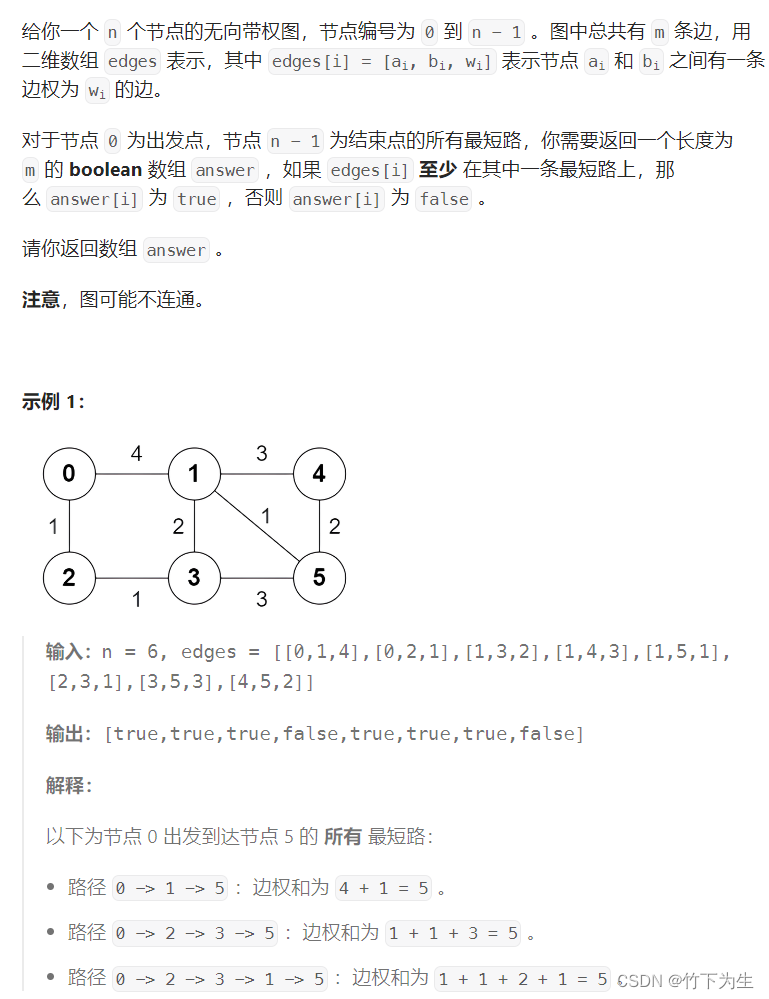
这题就是找最短路径经过的边，本质还是求最短路径(用Dijkstra算法)，只不过需要从最短路径逆推出它可能经过的边，代码如下

class Solution {
public:
    vector<bool> findAnswer(int n, vector<vector<int>>& edges) {
        vector<vector<tuple<int,int,int>>> g(n);
        int m = edges.size();
        for(int i=0;i<m;i++){
            auto e = edges[i];
            int x = e[0], y = e[1], w = e[2];
            g[x].emplace_back(y,w,i);
            g[y].emplace_back(x,w,i);
        }

        vector<long long>dist(n,LLONG_MAX);
        dist[0] = 0;
        priority_queue<pair<long long,int>> pq; // [d,i]
        pq.emplace(0,0);
        while(pq.size()){
            auto [d,i] = pq.top(); pq.pop();
            if(-d!=dist[i]) continue;
            for(auto [y,w,_]:g[i]){
                if(dist[y]>dist[i]+w){
                    dist[y] = dist[i]+w;
                    pq.emplace(-dist[y],y);
                }
            }
        }
        vector<bool> ans(m);
        if(dist[n-1]==LLONG_MAX)
            return ans;
        
        vector<bool> vis(n);
        function<void(int)>dfs=[&](int x){
            vis[x] = true;
            for(auto[y,w,i]:g[x]){
                if(dist[y]+w!=dist[x])
                    continue;
                ans[i] = true;
                if(!vis[y]) dfs(y);
            }
        };
        dfs(n-1);
        return ans;
    }
};