本文主要参考：

一文读懂ECDSA算法如何保护数据
椭圆曲线数字签名算法

1. ECDSA算法简介

  ECDSA 是 Elliptic Curve Digital Signature Algorithm 的简称，主要用于对数据（比如一个文件）创建数字签名，以便于你在不破坏它的安全性的前提下对它的真实性进行验证。
  你不应该将 ECDSA 与用来对数据进行加密的 AES（高级加密标准）相混淆。ECDSA 不会对数据进行加密、或阻止别人看到或访问你的数据，它可以防止的是确保数据没有被篡改。
  ECDSA 原理非常简单，有一个数学方程，在图上画了一条曲线，然后你在这条曲线上面随机选取了一个点作为你的 原点 G。接着你产生了一个 随机数 k，作为你的 私钥，最后你用上面的 随机数 k 和 原点 G 通过一些复杂的魔法数学方程得到该条曲线上面的第二个点，这是你的 公钥 P。

  当你想要对一个文件进行签名的时候，签名本身由两部分组成，称为 r 和 s 。通过 私钥k（随机数） 和文件的 哈希 组成一个魔法数学方程，这将给出你的签名的 s 部分。取 公钥 P 的 x 轴即为签名的 r 部分。为了验证签名的正确性，你需要 公钥 P 和签名 s、r组成一个魔法数学方程，该方程计算会得到一个坐标点，如果该坐标点的 x 轴刚好为签名中的 r，那么即可认为改签名是有效的。

2.椭圆曲线密钥生成

  像 $y^2=x^3+ax+b$ 这样的式子通常画出来是个椭圆曲线，如下图所示：

  画一条直线与椭圆曲线产生三个交点（P、Q、-R），我们称 P + Q = R，R 即为 -R 关于x轴的对称点（请注意这里的 + 实际指的是第三个交点的 x 轴对称点）。   若以椭圆曲线的某一切点 G 做一直线，则直线与椭圆曲线的另一交点即为 -2G，其关于x轴对称点即为 2G 点，若 2G 点与 G 点连接即可得到 3G 点，以此类推，即可得到 kG 点。   引入 G 点的好处是可以实现快速寻找，我们以 G 点做切线即可得到 2G 点，以 2G点为切线即可得到 4G 点，以此类推，这样的寻找过程，大大的减少了寻找次数。

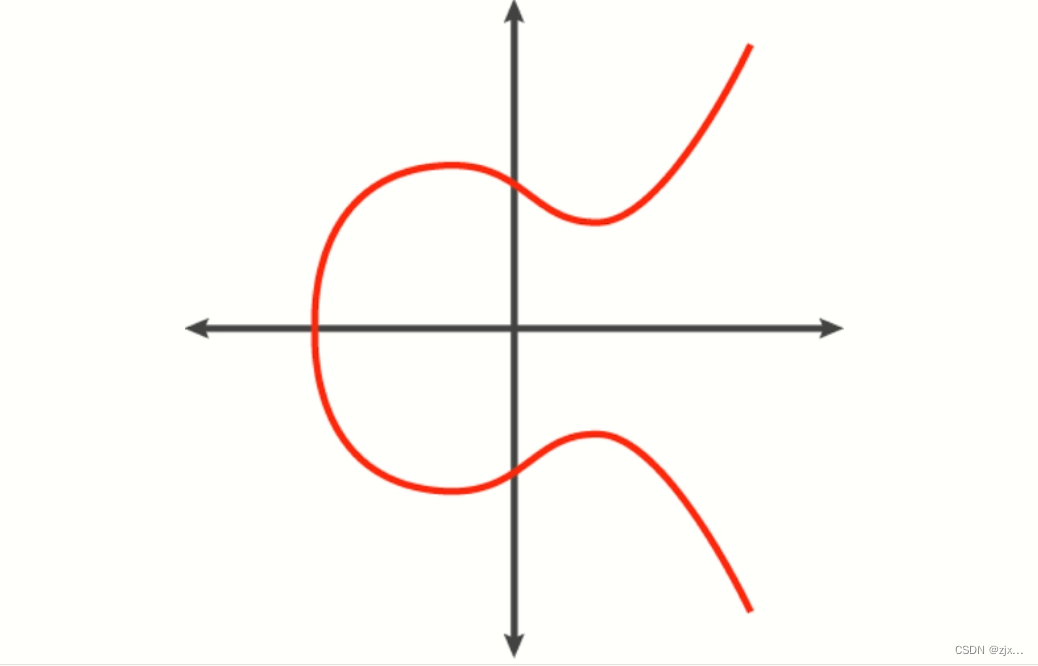
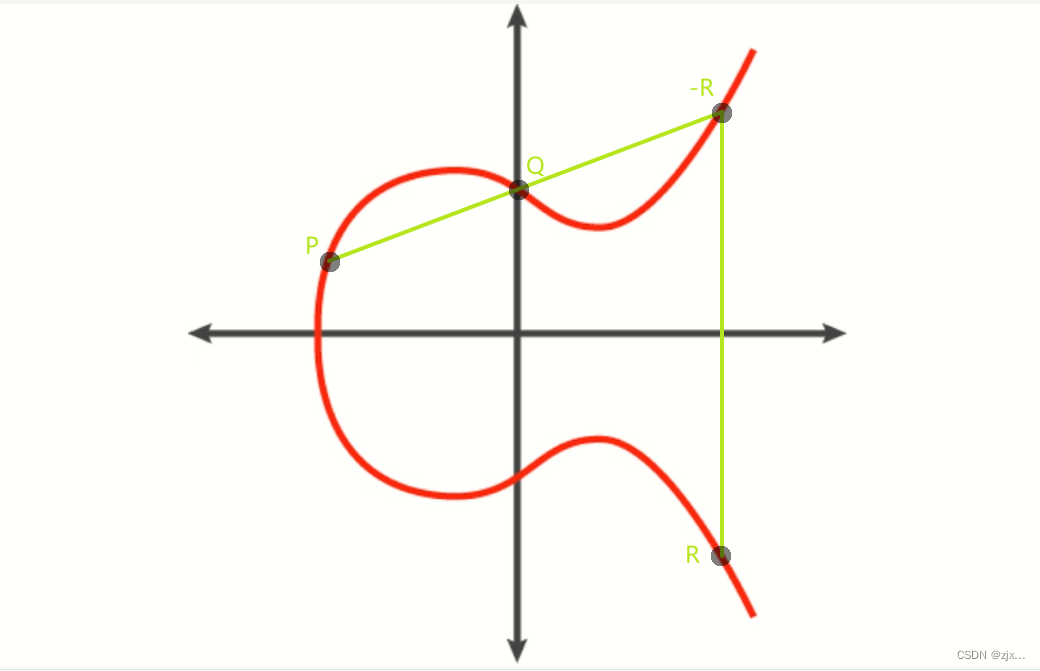
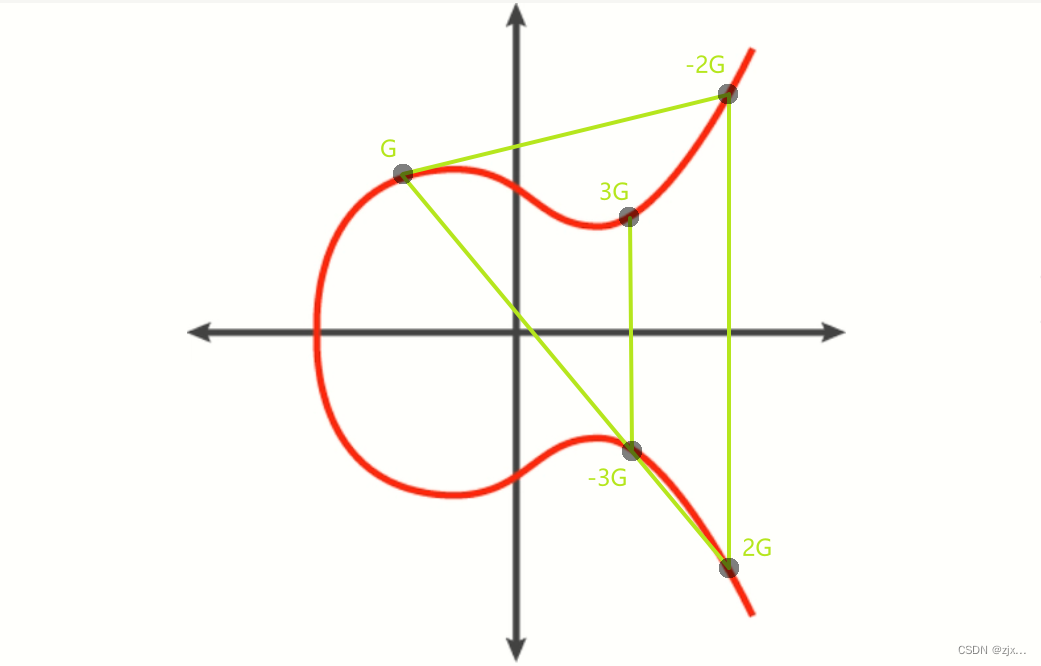
  椭圆曲线还有一个特性就是，我们以 G 为起点经过 k 次寻找后，得到 kG 点这一顺序计算过程是比较简单的，但如果我们已知 G 点要得到 kG 点是经过多少次寻找得到的是比较困难的，我们只能对 k 一个一个尝试，当 k 比较大时，k 的寻找过程是及其困难的，因此，这一过程是ECDSA算法背后安全性的基础，而这一原则也被称为 单向陷门函数。

比特币的椭圆曲线一般是采用以下函数：
$$y^2=x^3+7，a=0,b=7$$
开始的节点 Generator(G) 坐标为：
$$Gx=0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798$$
$$Gy=0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8$$
私钥 k 一般是选择比较大的随机数，通过开始节点 G 与私钥 k，我们即可得到公钥节点 P

3.椭圆曲线数字签名实现

  假设Alice要给Bob发送消息 M，Alice 根据 起始点 G 与选择的 随机数（私钥） k 可得到 公钥 P，然后用 私钥 k 与 要发送的消息M的哈希值 HASH(M) 相乘得到 s，然后将要发送的信息 M 与 s 一同发送给 Bob。Bob得到信息后，通过Alice的 公钥 P与 Hash(M) 相乘得到 Y，然后将 s 与 G 相乘得到X，如果X=Y则改签名即为有效，具体过程如下图所示：

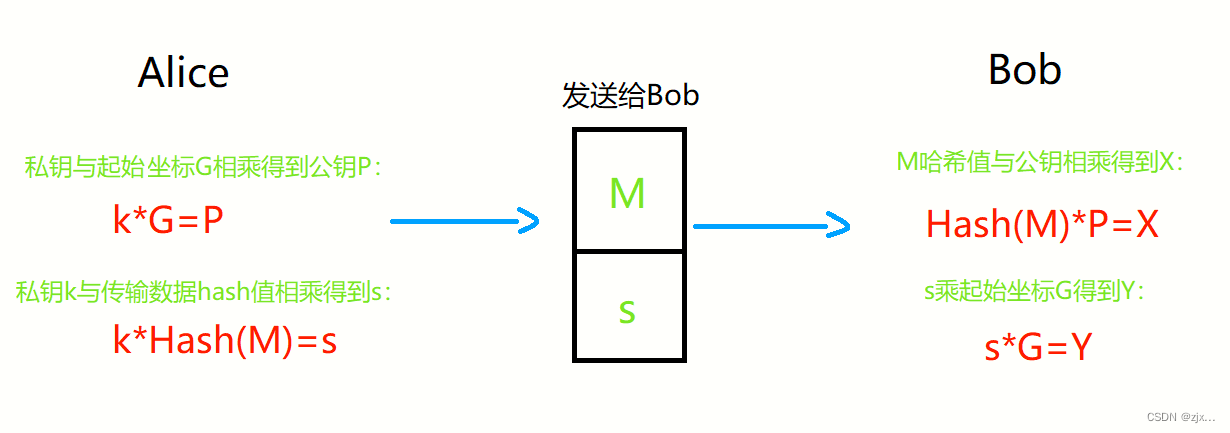
X=Y合理性证明：
$$X=Hash(M)\ast P=Hash(M)\ast k\ast G=s\ast G=Y$$
  虽然以上过程实现了数字签名，但是以上的签名过程是存在一定漏洞的，因为 Bob 得到的数据有 Alice 的公钥 P、s、以及起始坐标 G，根据 G 与 P 是推断不出私钥 k 的，但是 k 可由 s 计算得到 $k=s/Hash(M)$，因此，科学家为其又想了新的办法。

签名过程：

• 随机产生一个随机数 e ，通过计算得到 $eG=Q$，
• 随机产生一个随机数 k 作为私钥，计算得到 $kG=P$，$P$ 即为公钥，然后记录下 $P$ 的 $x$ 坐标记为 $r$。
• 利用 SHA1 计算要传递信息 $M$ 的哈希值 $z$。
• 利用方程 $s=(z+e\ast r)/k$ 计算得到 $s$。
• 要传递的数据即为 原始数据M 、M的Hash值z、r 与 s。

验证过程：

  计算 $\frac{z\ast G}{s}+\frac{r\ast Q}{s}=P$ ，若左右相等，则即为有效签名。

签名验证过程：

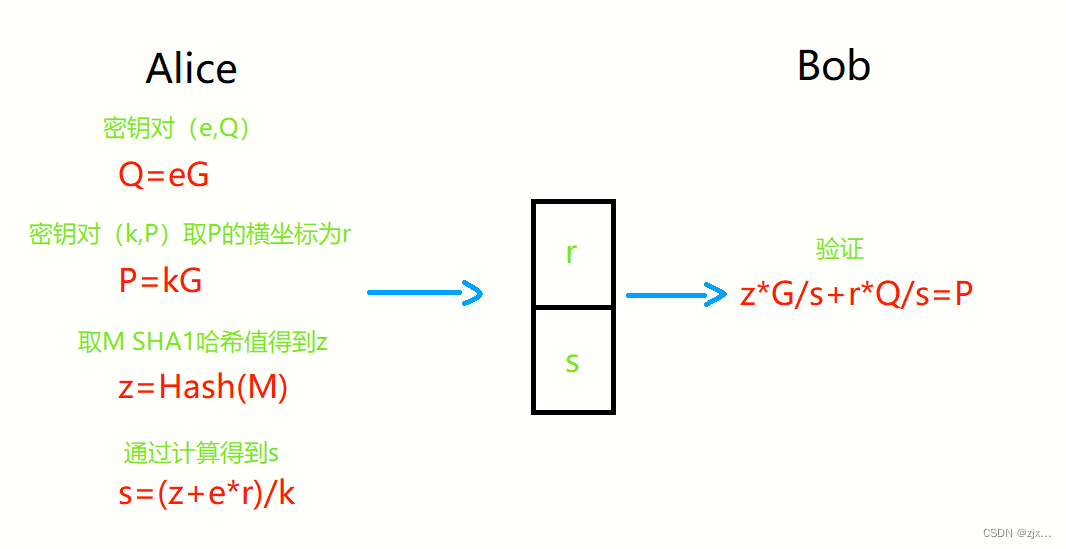
验证以上公式有效性：
$$\begin{array}{rl}\frac{z\ast G}{s}+\frac{r\ast Q}{s}& =\frac{z\ast G+r\ast Q}{s}\\ & =\frac{z\ast G+r\ast e\ast G}{s}\\ & =\frac{(z+r\ast e)\ast G}{s}\\ & =\frac{(z+r\ast e)\ast G\ast k}{(z+r\ast e)}\\ & =kG\\ & =P\end{array}$$
由于两侧求得的都为坐标，比较 x 轴即可。

  以上签名过程中被外界所指的参数有 公钥P、公钥Q、起始点G、r与s，我们可以看到在上面可由 s 求出密钥 k 的漏洞在现在的签名中不存在了，因为 $s=(z+e\ast r)/k$，其中有两个未知参数 e 与 k，所以此签名过程比上面的更加完备了。

  由于计算过程中所得数据要在规定的字节范围内，所以在实际代码中要进行取模运算。

4. 代码实现

  以下是使用 go 语言实现的ECDSA算法的签名与认证：
签名：

func (ecc *MyECC) Sign(msg []byte, secKey *big.Int) (*Signature, error) {
	// 随机产生随机数k作为私钥
	k,error := newRand()
	if error != nil {
		return nil, error
	}
	
	// 对要传递的消息msg进行hash运算得到z
	z_bytes := crypto.Keccak256(msg)
	z := new(big.Int).SetBytes(z_bytes)
	z.Mod(z, N)
	
	//计算得到私钥k的公钥P，并求出其x坐标作为r
	P := Multi(G,k)
	r := new(big.Int).Mod(P.X,N)
	
	// 计算要传递的参数s
	s := new(big.Int).Mul(r, secKey)
	s.Add(s, z)  
	s.Mul(s, Inv(k, N))  
	s.Mod(s, N)  

	// 传递s与r
	s_r := &Signature{s, r}

	return s_r, nil
}

验证：

func (ecc *MyECC) VerifySignature(msg []byte, signature *Signature, pubkey *Point) bool {
	// 获得s与r
	s, r := signature.s, signature.r
	
	// 获得传递信息msg的hash值z
	z_bytes := crypto.Keccak256(msg)
	z := new(big.Int).SetBytes(z_bytes)
	z.Mod(z, N)
	
	// 使用费马小定理求得1/s
	s_inv := Inv(s, N)
	
	// 取u = z/s
	u := new(big.Int).Mul(z,s_inv)
	u.Mod(u, N)
	
	// 取v = r/s
	v := new(big.Int).Mul(r,s_inv)
	v.Mod(v, N)
	
	// 计算u*G与v*Q
	uG := Multi(G,u)
	vQ := Multi(pubkey,v)

	// 计算u*G+v*Q得到R，并取出其x轴
	R := Add(uG,vP)
	Rx := new(big.Int).Mod(R.X,N)
	
	// 比较判断是否相同
	if Rx.Cmp(r)==0{
		return true
	}else{
		return false
	}

}