1. 数据流中的第 K 大元素
代码实现:
思路:创建一个大小为 k 的小顶堆,堆顶元素就是第 K 大元素
typedef struct { int *__data, *data; int size; int n; } KthLargest; #define swap(a, b) { \ __typeof(a) __c = (a); \ (a) = (b); \ (b) = __c; \ } // 从1开始存储,根结点下标为1 #define FATHER(i) ((i) / 2) #define LEFT(i) ((i) * 2) #define RIGHT(i) ((i) * 2 + 1) // 向上调整(非递归) void up_update(int *data, int i) { while (i > 1 && data[i] < data[FATHER(i)]) { swap(data[i], data[FATHER(i)]); i = FATHER(i); } } // 向下调整 void down_update(int *data, int i, int n) { while (LEFT(i) <= n) { int ind = i, l = LEFT(i), r = RIGHT(i); if (data[l] < data[ind]) { ind = l; } if (r <= n && data[r] < data[ind]) { ind = r; } if (ind == i) { break; } swap(data[i], data[ind]); i = ind; } } // 判满 bool full(KthLargest *p) { if (p == NULL || p->__data == NULL || p->n == p->size) { return true; } return false; } KthLargest* kthLargestCreate(int k, int *nums, int numsSize) { KthLargest *p = malloc(sizeof(KthLargest)); p->__data = malloc(sizeof(int) * k); p->data = p->__data - 1; p->size = k; p->n = 0; // 入堆 for (int i = 0; i < numsSize; i++) { if (full(p)) { // 堆满 if (nums[i] > p->data[1]) { p->data[1] = nums[i]; // 向下调整 down_update(p->data, 1, p->n); } } else { // 堆没满 p->n++; p->data[p->n] = nums[i]; up_update(p->data, p->n); } } return p; } int kthLargestAdd(KthLargest *obj, int val) { if (full(obj)) { // 堆满 if (obj->data[1] < val) { // val > 堆顶元素 obj->data[1] = val; // 向下调整 down_update(obj->data, 1, obj->n); } } else { // 堆没满 obj->n++; obj->data[obj->n] = val; // 向上调整 up_update(obj->data, obj->n); } return obj->data[1]; } void kthLargestFree(KthLargest *obj) { if (obj == NULL) { return; } free(obj->__data); free(obj); } /** * Your KthLargest struct will be instantiated and called as such: * KthLargest* obj = kthLargestCreate(k, nums, numsSize); * int param_1 = kthLargestAdd(obj, val); * kthLargestFree(obj); */
2. 数据流的中位数
代码实现:
堆排序——超时
typedef struct { int *__data, *data; int n; } MedianFinder; #define swap(a, b) { \ __typeof(a) __c = (a); \ (a) = (b); \ (b) = __c; \ } // 从1开始存储,根结点下标为1 #define FATHER(i) ((i) / 2) #define LEFT(i) ((i) * 2) #define RIGHT(i) ((i) * 2 + 1) // 向上调整(非递归) void up_update_2(int *data, int i) { while (i > 1 && data[i] > data[FATHER(i)]) { swap(data[i], data[FATHER(i)]); i = FATHER(i); } } // 向下调整 void down_update(int *data, int i, int n) { while (LEFT(i) <= n) { int ind = i, l = LEFT(i), r = RIGHT(i); if (data[l] > data[ind]) { ind = l; } if (r <= n && data[r] > data[ind]) { ind = r; } if (ind == i) { break; } swap(data[i], data[ind]); i = ind; } } MedianFinder* medianFinderCreate() { MedianFinder *p = malloc(szieof(MedianFinder)); p->__data = malloc(sizeof(int) * 50000); p->data = p->__data - 1; p->n = 0; return p; } // 将大顶堆调整成从小到大排序 void heap_sort_final(int *data, int n) { if (data == NULL) { return; } for (int i = n; i >= 2; i--) { swap(data[1], data[i]); down_update(data, 1, i - 1); // 向下调整 } } void medianFinderAddNum(MedianFinder *obj, int num) { obj->n++; obj->data[obj->n] = num; for (int i = obj->n / 2; i >= 1; i--) { down_update(obj->data, i, obj->n); } heap_sort_final(obj->data, obj->n); } double medianFinderFindMedian(MedianFinder *obj) { if (obj->n % 2) { // 奇数 return obj->data[obj->n / 2 + 1]; } int l = obj->n / 2, r = l + 1; return 1.0 * (obj->data[l] + obj->data[r]) / 2; } void medianFinderFree(MedianFinder *obj) { if (obj == NULL) { return; } free(obj->__data); free(obj); } /** * Your MedianFinder struct will be instantiated and called as such: * MedianFinder* obj = medianFinderCreate(); * medianFinderAddNum(obj, num); * double param_2 = medianFinderFindMedian(obj); * medianFinderFree(obj); */
3. 丑数 ||
代码实现:
最小堆
初始时堆为空。首先将最小的丑数 1 加入堆
每次取出堆顶元素 x,则 x 是堆中最小的丑数,由于 2x, 3x, 5x 也是丑数,因此将 2x, 3x, 5x 加入堆
上述做法会导致堆中出现重复元素的情况。为了避免重复元素,可以使用哈希集合去重,避免相同元素多次加入堆
在排除重复元素的情况下,第 n 次从最小堆中取出的元素即为第 n 个丑数
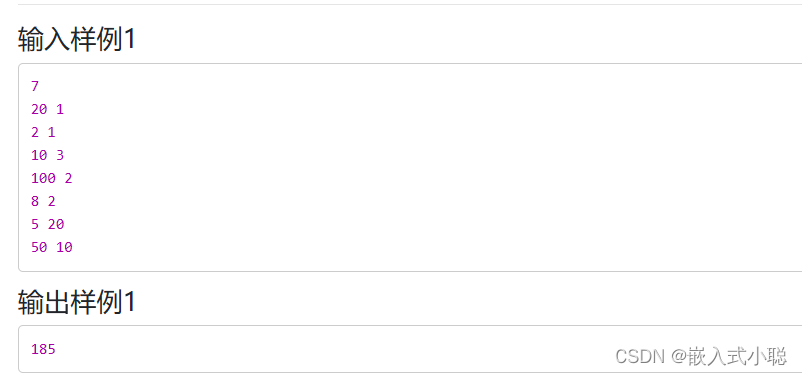
4. 超市卖货
代码实现: