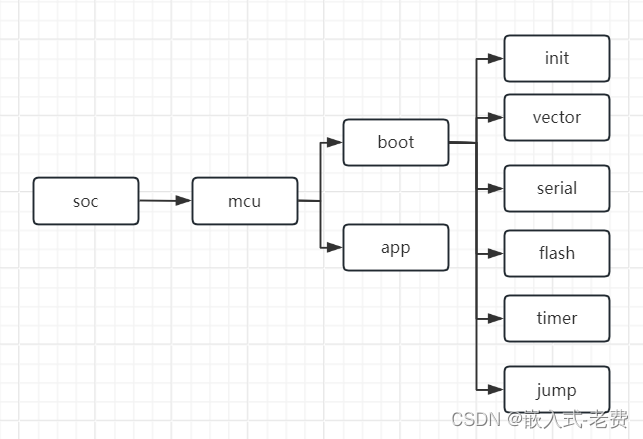
一、物理结构和逻辑结构
在内存中的存储结构,逻辑结构为想象出来的存储结构。
二、完全二叉树的顺序存储结构
parent = (child - 1)/2
leftchild = 2*parent + 1;
rightchild = 2*parent +2
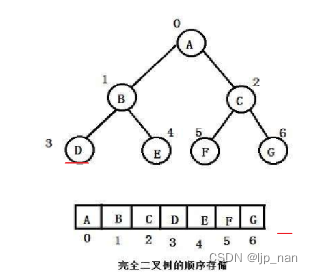
上面的顺序结构只适合存储完全二叉树。如果存储,会浪费很多的空间。
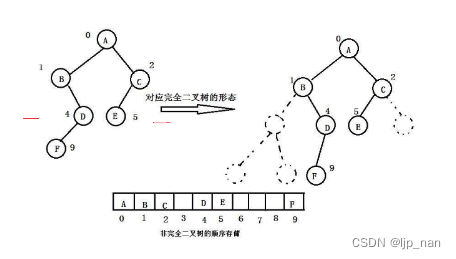
三、堆
1、堆的分类
小根堆:树中所有的父亲都小于或等于孩子。
大根堆:树中所有的父亲都大于或等于孩子。

接下来我们需要定义一个堆。定义过程如下:
创建堆的时候会涉及到一个向上调整的算法:我们可以画图表示这一过程
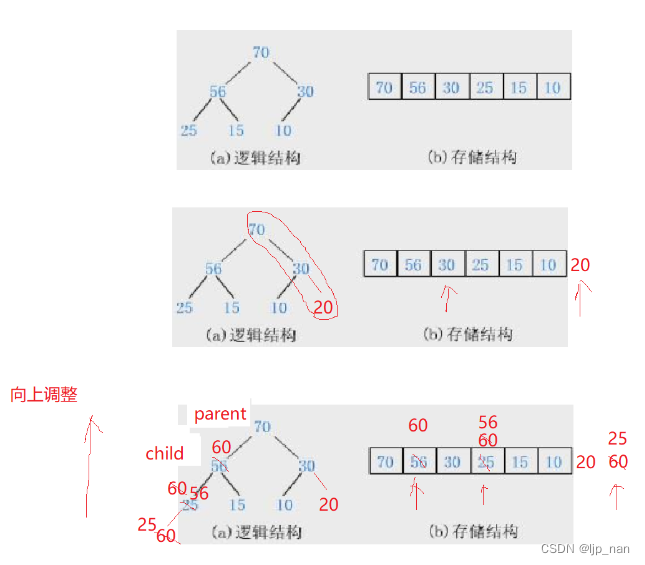
void UpAdjust(HPDataType* a, int child)
{
assert(a);
int parent = (child - 1) / 2;
//建立大堆
while (child > 0)
{
if (a[child] > a[parent])
{
//交换两个数字
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}删除堆顶数据需要涉及到向下调整
这里不能挪动数据。原因有两个,效率低下,父子兄弟关系全乱了。
思路就是:把头部数据和尾部数据交换。删除尾部数据,然后进行向下调整
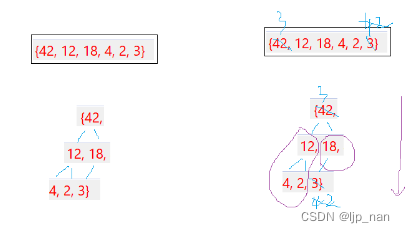
这样删除的优点是 效率高,保持了大部分堆的父子关系。
向下调整的过程中我们需要和儿子中最大的进行比较。这样才能保证堆的关系不变。
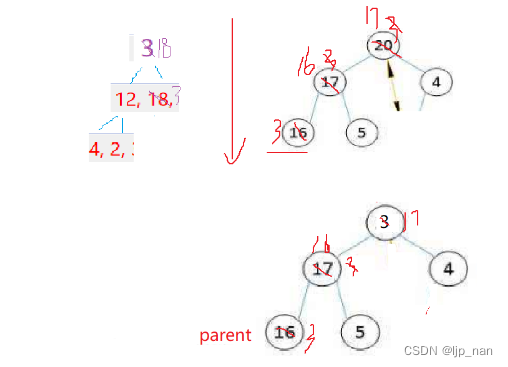
没有孩子时结束,转换一下就是child < size。
void DownAdjust(HPDataType* a,int parent,int size)
{
int child = 2 * parent + 1;
while (child < size)
{
//选出最大的那一个孩子
if (child + 1 < size && a[child] < a[child + 1])
{
child++;
}
if (a[child] > a[parent])
{
//交换两个数字
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}整体实现
#include "heap.h"
void HeapInit(HP* hp)
{
assert(hp);
hp->a = (HPDataType*)malloc(sizeof(HPDataType) * SIZE);
hp->size = 0;
hp->capacity = SIZE;
}
void AddCapacity(HP* hp)
{
assert(hp);
if (hp->size == hp->capacity)
{
HPDataType* temp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * hp->capacity * 2);
if (temp == NULL)
{
perror("realloc failed");
return;
}
hp->a = temp;
hp->capacity *= 2;
}
}
void Swap(int* left, int* right)
{
int temp = *left;
*left = *right;
*right = temp;
}
//除了child的位置,前面的数据构成堆
void UpAdjust(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
//建立大堆
while (child > 0)
{
if (a[child] > a[parent])
{
//交换两个数字
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapPush(HP* hp, HPDataType x)
{
//考虑扩容的问题
AddCapacity(hp);
//插入数据
hp->a[hp->size++] = x;
//还需要考虑向上调整的问题。
UpAdjust(hp->a, hp->size - 1);
}
void DownAdjust(HPDataType* a,int parent,int size)
{
int child = 2 * parent + 1;
while (child < size)
{
//选出最大的那一个孩子
if (child + 1 < size && a[child] < a[child + 1])
{
child++;
}
if (a[child] > a[parent])
{
//交换两个数字
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
//删除头部的数据
void HeapPop(HP* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
//首先交换头和尾的数字
Swap(&hp->a[0], &hp->a[hp->size-1]);
//然后删除尾的数字
hp->size--;
//向下调整恢复堆的原型 向下调整的左右子树一定是堆
DownAdjust(hp->a, 0, hp->size);
}
HPDataType HeapTop(HP* hp)
{
assert(hp);
return hp->a[0];
}
bool HeapEmpty(HP* hp)
{
assert(hp);
return hp->size == 0;
}
int HeapSize(HP* hp)
{
assert(hp);
return hp->size;
}四、堆排
对数组进行排序。我们可以把它直接搞成一个堆,建堆操作
1、向上调整建堆
(1)把第一个数看成一个堆中的数。后来的数进行向上调整建立堆。 O(nlogn)
(2)排升序需要建大堆,减小堆关系就都乱了

利用向上调整建大堆时我们可以交换堆头和堆尾的值。然后在进行向下调整选出次小的值,如此往复。
堆排的过程如下
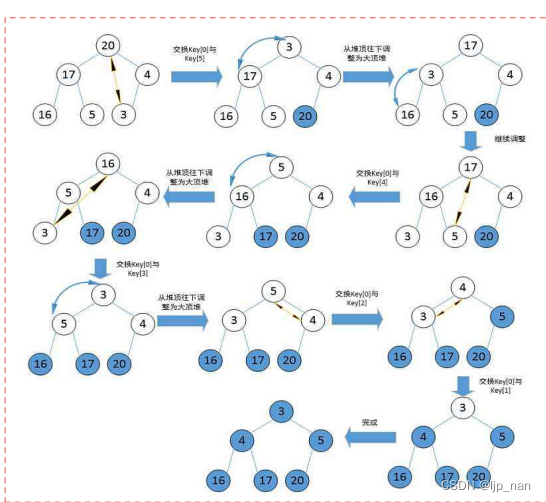
堆排代码:
void HeapSort(int* a,int n)
{
//首先建立大堆
for (int i = 1; i < n; i++)
{
UpAdjust(a, i);
}
//交换堆头和堆尾的数字选出最大的数字放到堆尾
//然后向下调整
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
DownAdjust(a, 0, end);
end--;
}
}