目录
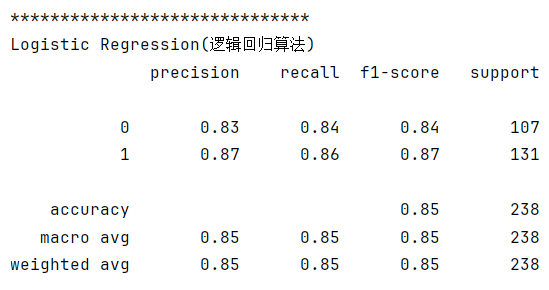
6.1 为什么正确率有时不能有效评估分类算法?
6.2 什么样的分类器最好?
6.3 什么是聚类,你知道哪些聚类算法?
6.4 K-Means聚类算法如何调优?
6.5 K-Means聚类算法如何选择初始点?
6.6 K-Means聚类聚的是特征还是样本
6.7 K-Means++

欢迎大家订阅我的专栏一起学习共同进步,主要针对25届应届毕业生
祝大家早日拿到offer! let's go
http://t.csdnimg.cn/lSA8k
| 算法类别 | 优点 | 缺点 |
| Bayes | 1) 所需估计的参数少,对于缺失数据不敏感 | 1)需要假设属性之间相互独立,这往往并不成立(喜欢吃番茄、鸡蛋,却不喜欢吃番茄炒蛋) |
| SVM | 1)可以解决小样本下机器学习的问题 | 1)对缺失数据敏感 |
| KNN | 1)思想简单,理论成熟,既可以用来做分类也可以用来做回归 | 1)计算量太大 |
| Logistic Regression | 1)速度快 | 1)特征处理复杂,需要归一化和较多的特征工程 |
| Neural Network | 1)分类准确率高 | 1)需要大量参数(网络拓扑、阀值、阈值) |
6.1 为什么正确率有时不能有效评估分类算法?
假设我们正在开发一个模型来诊断罕见疾病。在这种情况下,罕见疾病的发病率可能非常低,例如仅占所有病例的百分之一。因此,我们的数据集中会有大量的健康样本(类别0),而罕见疾病的样本数量相对较少(类别1)。
现在假设我们开发了一个简单的模型,该模型倾向于将所有样本都预测为健康(类别0),因为这样可以获得很高的整体准确率。然而,对于罕见疾病的样本,这样的模型将无法提供有效的诊断,因为它几乎总是预测为健康。
在这种情况下,我们需要采取措施来解决数据不平衡问题,确保模型能够在诊断罕见疾病时具有良好的性能。我们可以使用类似于前面提到的解决方案,例如重采样、类别权重调整、使用不同的评价指标等来处理数据不平衡。
出现这种现象的原因主要是数据分布不均衡,类别为1的数据太少,错分了类别1但达到很高的正确率,此时失效。
6.2 什么样的分类器最好?
在确保一定正确率前提下,要求分类器的召回率尽量高。
6.3 什么是聚类,你知道哪些聚类算法?
什么是聚类:
- 聚类是按照某个特定标准把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
主要可划分为:
- K-Means聚类
- 均值漂移聚类
- 基于密度的空间聚类算法
- 高斯混合模型的期望最大化聚类
- 凝聚层次聚类
K-Means聚类
- 基本K-Means算法的思想很简单,事先确定常数K,常数K意味着最终的聚类类别数,首先随机选定初始点为质心,并通过计算每一个样本与质心之间的相似度(这里为欧式距离),将样本点归到最相似的类中,接着,重新计算每个类的质心(即为类中心),重复这样的过程,直到质心不再改变,最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度,故在大规模的数据集上,K-Means算法的收敛速度比较慢。
K-means 聚类流程:
- 首先确定一个k值,即希望将数据集经过聚类得到k个集合。
- 从数据集中随机选择k个数据点作为质心。
- 对数据集中每一个点,计算其与每一个质心的距离(如欧式距离),离哪个质心近,就划分到那个质心所属的集合。
- 把所有数据归好集合后,一共有k个集合。然后重新计算每个集合的质心。
- 如果新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为聚类已经达到期望的结果,算法终止。
- 如果新质心和原质心距离变化很大,需要迭代3~5步骤
6.4 K-Means聚类算法如何调优?
- 数据归一化和离群点的处理
k-means是根据欧式距离来度量数据的划分,均值和方差大的数据会对结果有致命的影响。同时,少量的噪声也会对均值产生较大的影响,导致中心偏移。所以在聚类前一定要对数据做处理。 - 选择合适的k值:k-means++方法,在一开始确定簇时,让所有簇中心坐标两两距离最远。
6.5 K-Means聚类算法如何选择初始点?
初始点随机分布
k-means++方法:在一开始确定簇时,让所有簇中心坐标两两距离最远
6.6 K-Means聚类聚的是特征还是样本
聚的是特征。
- 聚类的核心思想是将具有相似特征的事物给聚在一起,也就是说聚类算法最终只能告诉我们哪些样本属于同一个类别,而不能告诉我们每个样本具体属于什么类别。
6.7 K-Means++
K-means与K-means++:原始K-means算法最开始随机选取数据集中K个点作为聚类中心,而K-means++按照如下的思想选取K个聚类中心:假设已经选取了n个初始聚类中心(0<n<K),则在选取第n+1个聚类中心时:距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。在选取第一个聚类中心(n=1)时同样通过随机的方法。可以说这也符合我们的直觉:聚类中心当然是互相离得越远越好。这个改进虽然直观简单,但是却非常得有效。
k-means code:
import numpy as np
np.random.seed(545)
def wh_iou(wh1, wh2):
# 返回nxm的IoU矩阵。wh1是nx2的数组,wh2是mx2的数组
wh1 = wh1[:, None] # [N,1,2]
# 通过添加维度将输入的边界框数组 wh1 和 wh2 转换为三维数组
wh2 = wh2[None] # [1,M,2]
inter = np.minimum(wh1, wh2).prod(2) # [N,M]
# 这一行代码计算了交集部分的面积。它首先对 wh1 和 wh2 中的对应元素进行逐元素的最小值计算,然后对第二个维度进行乘积运算。
return inter / (wh1.prod(2) + wh2.prod(2) - inter) # iou = inter / (area1 + area2 - inter)
# wh1.prod(2) 和 wh2.prod(2) 计算了 wh1 和 wh2 中每个边界框的面积
def k_means(boxes, k, dist=np.median):
"""
YOLO的k-means聚类方法
参考: https://github.com/qqwweee/keras-yolo3/blob/master/kmeans.py
参数:
boxes: 需要进行聚类的边界框
k: 聚类中心的数量
dist: 更新聚类中心的方法(默认为中位数,效果略优于均值)
"""
box_number = boxes.shape[0]
last_nearest = np.zeros((box_number,))
# 创建一个长度为 box_number 的零数组,用于存储上一次迭代时每个边界框所属的最近的聚类中心的索引。在算法的每次迭代中,都会将当前迭代的结果与上一次迭代的结果进行比较,以判断是否达到了收敛条件,从而决定是否终止迭代。
# 随机选择k个边界框作为初始聚类中心
clusters = boxes[np.random.choice(box_number, k, replace=False)] # replace 不重复的选取
print((clusters))
while True:
# 计算每个边界框到每个聚类中心的距离: 1-IOU(边界框, 聚类中心)
distances = 1 - wh_iou(boxes, clusters)
# 找到每个边界框最近的聚类中心
current_nearest = np.argmin(distances, axis=1)
# 如果聚类结果不再变化,则退出循环(收敛)
if (last_nearest == current_nearest).all():
break
# 根据每个聚类中的边界框更新聚类中心
for cluster in range(k):
clusters[cluster] = dist(boxes[current_nearest == cluster], axis=0)
last_nearest = current_nearest
return clusters
if __name__ == '__main__':
boxes = np.array([[10, 20],
[15, 25],
[30, 35],
[40, 45],
[50, 55],
[60, 65]])
# Number of clusters
k = 2
# Call k_means function
clusters = k_means(boxes, k)
print("Cluster centers:\n", clusters)